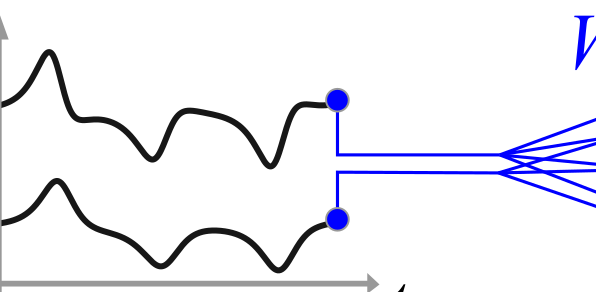
We demonstrate that matching the symmetry properties of a reservoir computer (RC) to the data being processed dramatically increases its processing power. We apply our method to the parity task, a challenging benchmark problem that highlights inversion and permutation symmetries, and to a chaotic system inference task that presents an inversion symmetry rule. For the parity task, our symmetry-aware RC obtains zero error using an exponentially reduced neural network and training data, greatly speeding up the time to result and outperforming hand crafted artificial neural networks. When both symmetries are respected, we find that the network size $N$ necessary to obtain zero error for 50 different RC instances scales linearly with the parity-order $n$. Moreover, some symmetry-aware RC instances perform a zero error classification with only $N=1$ for $n\leq7$. Furthermore, we show that a symmetry-aware RC only needs a training data set with size on the order of $(n+n/2)$ to obtain such performance, an exponential reduction in comparison to a regular RC which requires a training data set with size on the order of $n2^n$ to contain all $2^n$ possible $n-$bit-long sequences. For the inference task, we show that a symmetry-aware RC presents a normalized root-mean-square error three orders-of-magnitude smaller than regular RCs. For both tasks, our RC approach respects the symmetries by adjusting only the input and the output layers, and not by problem-based modifications to the neural network. We anticipate that generalizations of our procedure can be applied in information processing for problems with known symmetries.
翻译:我们证明,将储油层计算机(RC)的对称特性与正在处理的数据相匹配,会大大提高其处理能力。当两个对称都得到尊重时,我们发现,一个具有挑战性的基准问题,即突出反转和对调对称对称的具有挑战性的基准问题,以及一个显示反转对称对称规则的混乱的系统推导任务。对于对称任务,我们的对称识RC使用指数性下降的神经网络和培训数据获得零误差,大大加快了产生和完成手制人工神经网络的时间。当两个对称都受到尊重时,我们发现,在50个不同的对称对称对称的对等任务中,要获得零误差的对称是具有挑战性的基准问题。此外,一些对称对称的对称RC(RC)的对称只进行零差分数分类,只有1N=1美元用于美元用于计算 $leq7美元。此外,我们显示,一个对称的RC(n+2.5美元)的对等分数仅需要一组的培训数据,才能获得这种性能的对等值,对于50美元进行更小的对等的对等的对价处理,要与2美元。