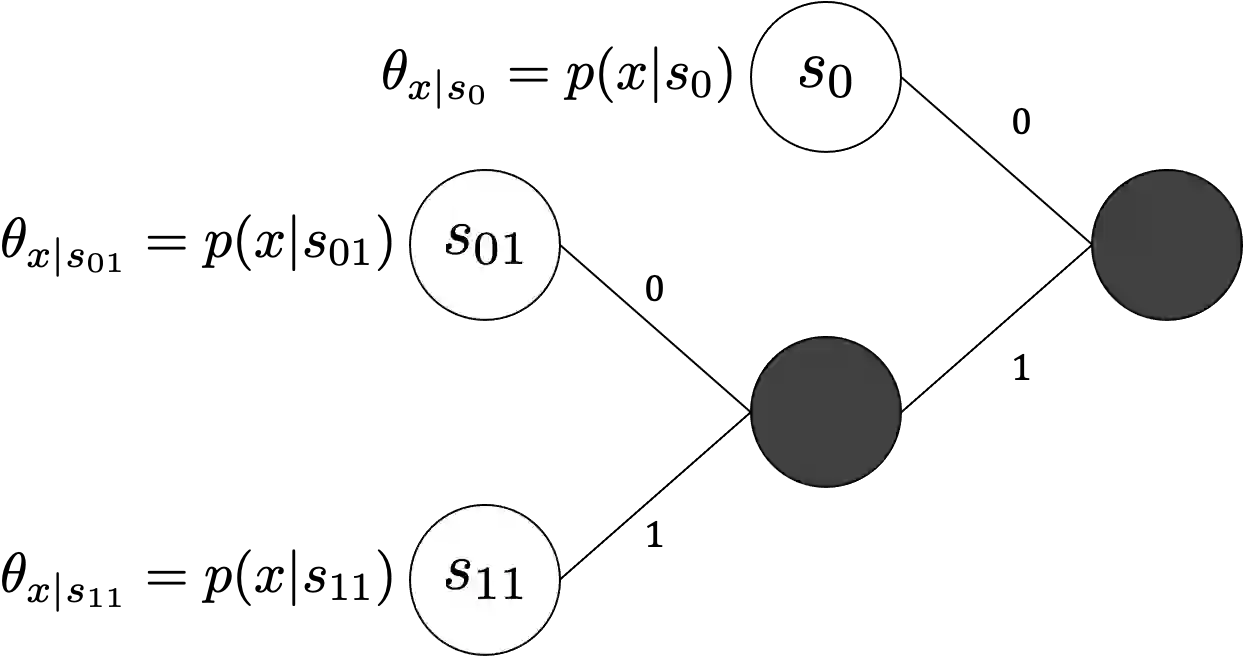
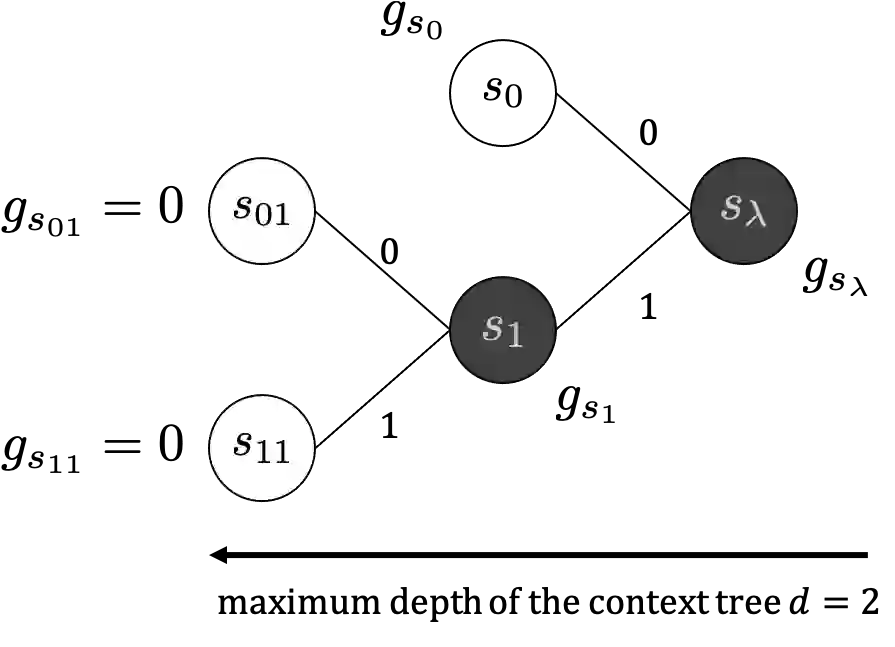
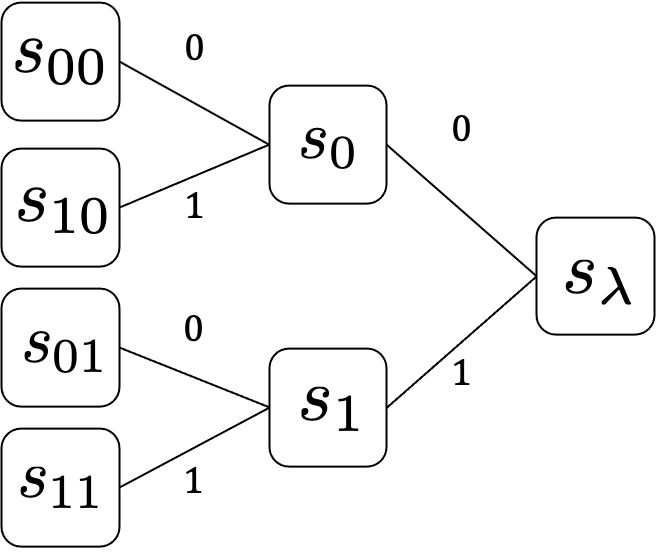
The context tree source is a source model in which the occurrence probability of symbols is determined from a finite past sequence, and is a broader class of sources that includes i.i.d. and Markov sources. The proposed source model in this paper represents that a subsequence in each interval is generated from a different context tree model. The Bayes code for such sources requires weighting of the posterior probability distributions for the change patterns of the context tree source and for all possible context tree models. Therefore, the challenge is how to reduce this exponential order computational complexity. In this paper, we assume a special class of prior probability distribution of change patterns and context tree models, and propose an efficient Bayes coding algorithm whose computational complexity is the polynomial order.
翻译:上下文树源是一个源模型,其符号的发生概率是根据有限的过去序列确定的,并且是一个更广泛的来源类别,包括i.d.和Markov来源。本文件中拟议的源模型表明,每个间距的子序列是由不同的上下文树模型产生的。这些源的贝斯代码要求对上下文树源的变化模式和所有可能的上下文树模型的事后概率分布进行加权。因此,挑战是如何减少指数顺序的计算复杂性。在本文件中,我们假定了变化模式和上下文树模型的先前概率分布的特殊类别,并提出了一个高效的贝斯编码算法,其计算复杂性是多数值顺序。