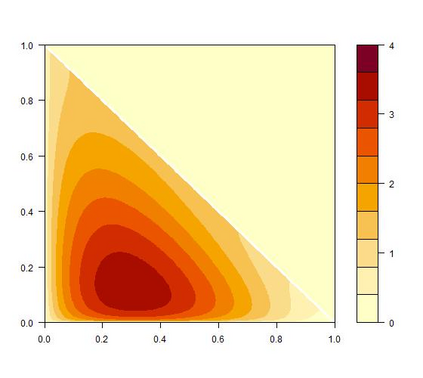
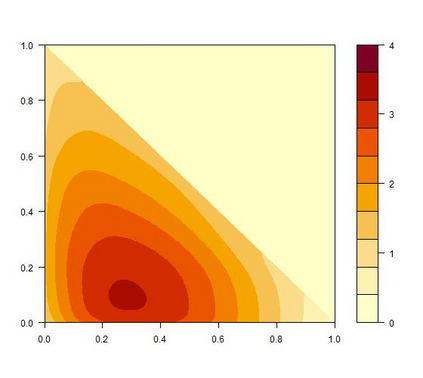
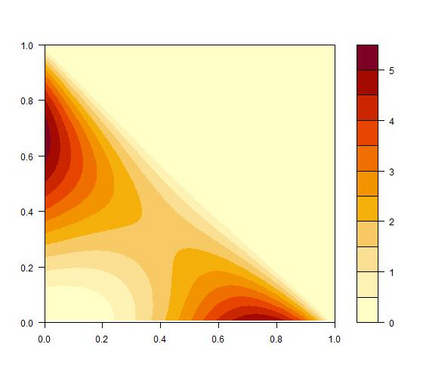
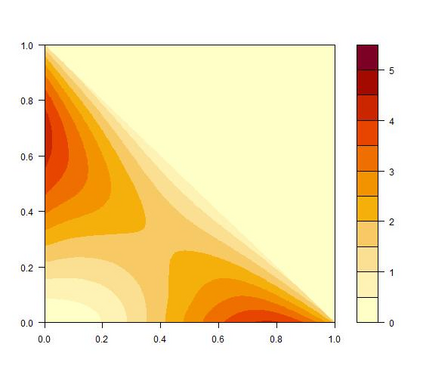
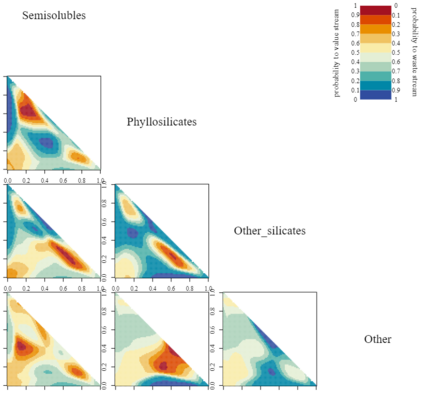
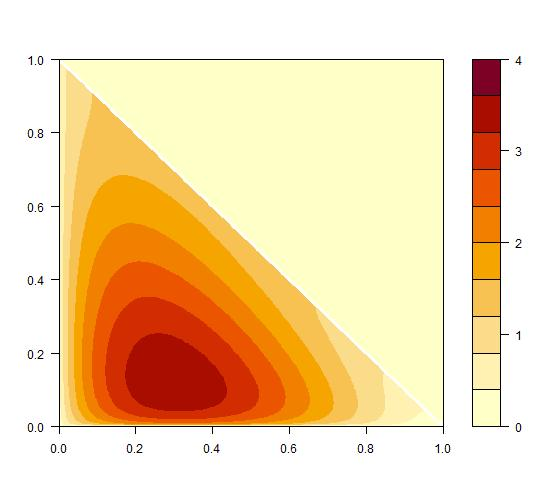
We study theoretically, for the first time, the Dirichlet kernel estimator introduced by Aitchison and Lauder (1985) for the estimation of multivariate densities supported on the $d$-dimensional simplex. The simplex is an important case as it is the natural domain of compositional data and has been neglected in the literature on asymmetric kernels. The Dirichlet kernel estimator, which generalizes the (non-modified) unidimensional Beta kernel estimator from Chen (1999), is free of boundary bias and non-negative everywhere on the simplex. We show that it achieves the optimal convergence rate $O(n^{-4/(d+4)})$ for the mean squared error and the mean integrated squared error, we prove its asymptotic normality and uniform strong consistency, and we also find an asymptotic expression for the mean integrated absolute error. To illustrate the Dirichlet kernel method and its favorable boundary properties, we present a case study on minerals processing.
翻译:我们第一次从理论上研究了Aitchison和Lauder(1985年)提出的Drichlet 内核估计值,用于估算以美元-维简单x支持的多变量密度。简单x是一个重要案例,因为它是组成数据的自然领域,在关于不对称内核的文献中被忽略。Drichlet 内核估计值是陈(1999年)的(非修改的)单维Beta内核测量器,它没有边界偏差,也没有在简单x的任何地方出现偏差。我们表明,它实现了平均正方差和平均合并方差的最佳趋同率$O(n ⁇ -4/(d+4}),我们证明了它无症状的正常性和统一性,我们也发现一个表示(非修改的)单一的绝对误差的无症状。为了说明Drichlet内核方法及其有利的边界特性,我们介绍了一项关于矿物加工的案例研究。