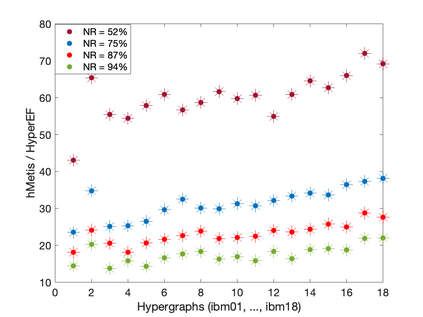
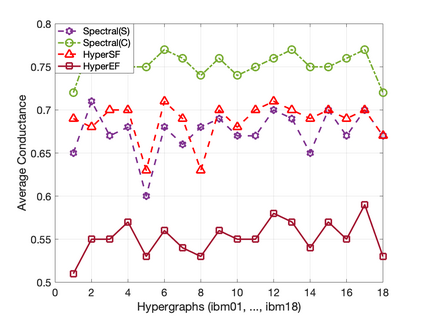
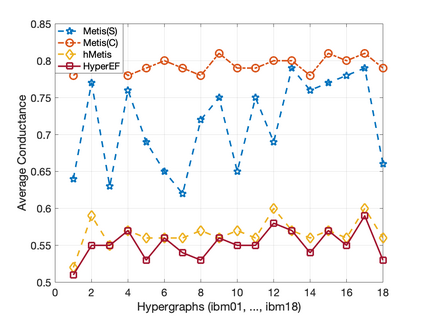
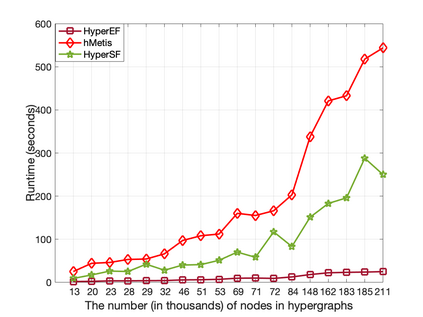
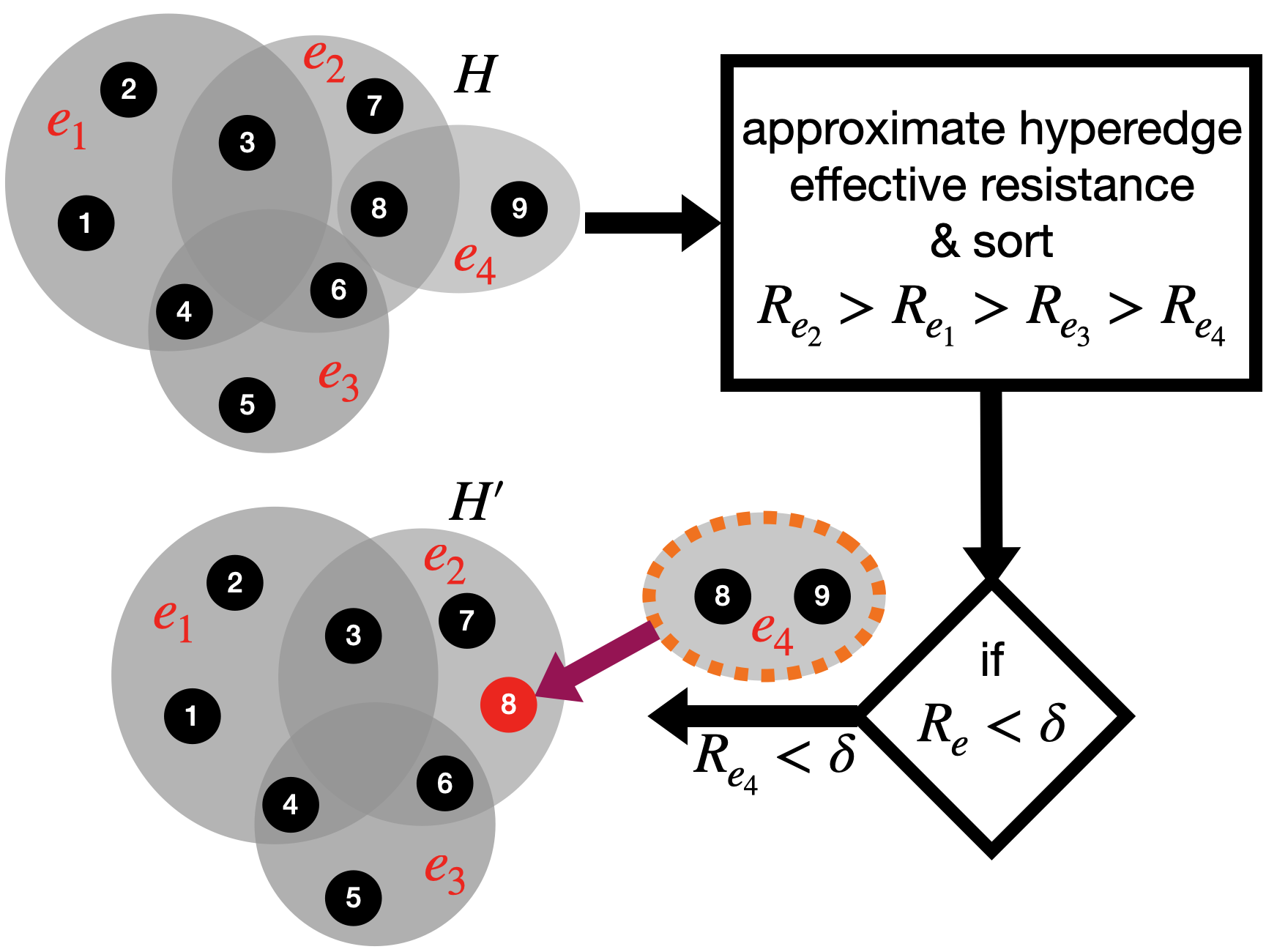
This paper introduces a scalable algorithmic framework (HyperEF) for spectral coarsening (decomposition) of large-scale hypergraphs by exploiting hyperedge effective resistances. Motivated by the latest theoretical framework for low-resistance-diameter decomposition of simple graphs, HyperEF aims at decomposing large hypergraphs into multiple node clusters with only a few inter-cluster hyperedges. The key component in HyperEF is a nearly-linear time algorithm for estimating hyperedge effective resistances, which allows incorporating the latest diffusion-based non-linear quadratic operators defined on hypergraphs. To achieve good runtime scalability, HyperEF searches within the Krylov subspace (or approximate eigensubspace) for identifying the nearly-optimal vectors for approximating the hyperedge effective resistances. In addition, a node weight propagation scheme for multilevel spectral hypergraph decomposition has been introduced for achieving even greater node coarsening ratios. When compared with state-of-the-art hypergraph partitioning (clustering) methods, extensive experiment results on real-world VLSI designs show that HyperEF can more effectively coarsen (decompose) hypergraphs without losing key structural (spectral) properties of the original hypergraphs, while achieving over $70\times$ runtime speedups over hMetis and $20\times$ speedups over HyperSF.
翻译:本文引入了一个可测量的算法框架( Hyperef ), 用于利用超强有效抗力, 利用超强抗力, 将大型超强的光谱剖析( 分解) 。 受最近低抗力- 直径分解简单图形的理论框架的驱动, 超强F2 旨在将大型超强分解成多个节点集群, 且只有几个跨集层的顶端。 超高端F2的关键部分是用于估计超尖端有效抗力的近线性时间算法, 从而可以纳入高空图上定义的最新基于扩散的非线性非线性二次二次二次曲线操作。 为了实现良好的运行时间可变性, 在 Krylov 亚空基空间( 或大约为eigensubspace ) 内进行超高抗力分解的超精度搜索, 将高光速超超超标超标超标超标超标超标的超标超标超标( 超标) 超标超标超标超标的超标 超标 超标 超标 超标 超标 超标 超标 超标 超标 超标 超标 超标 超标, 超标 超标 的 超标 超标 超标 超标 的 超标 超标 超标 超标 超标 的超标 的 超标 的 超标 超标 超标 超标 基 的 基 基 的 的 基 基 基 基 基 基 基 的 基 基 基 基 基 基 的 的 的 的 的 的 的 基 基 的 的 的 基 的 的 基 基 基 的 的 的 基 的 的 基 的 的 的 的 的 的 的 的 的 的 的 的 的 的 高程 基 基 的 的 基 基 基 的 的 的 的 的 的 高程 的 高程 高程 高程 的 基 基