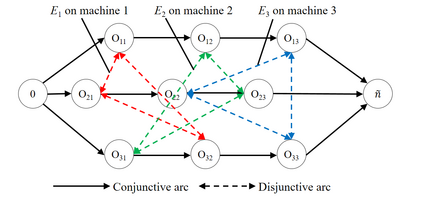
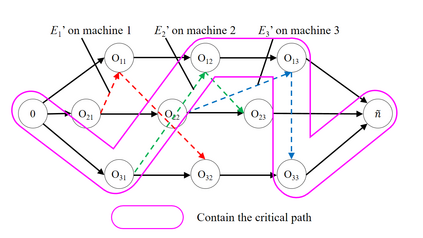
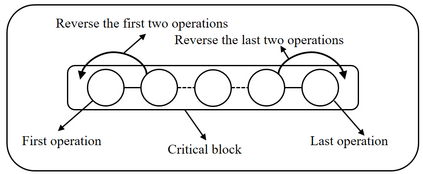
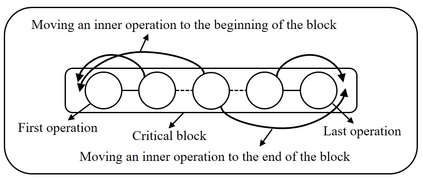
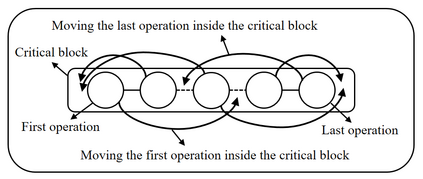
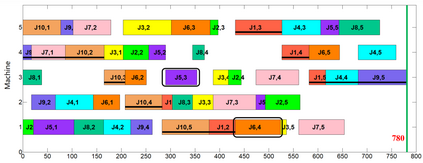
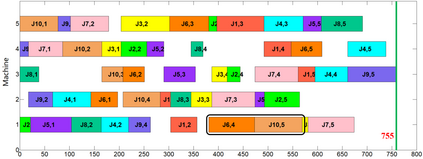
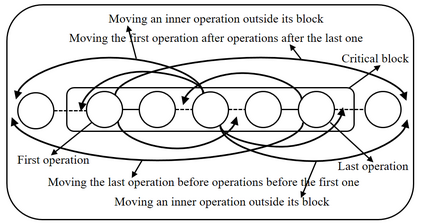
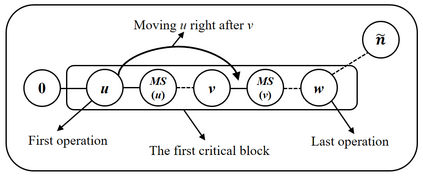
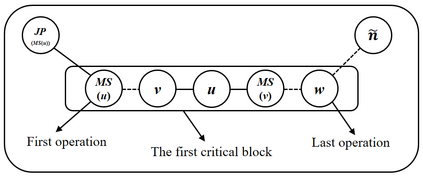
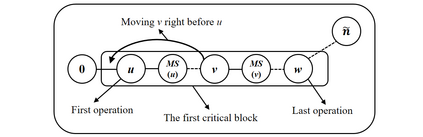
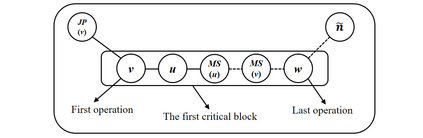
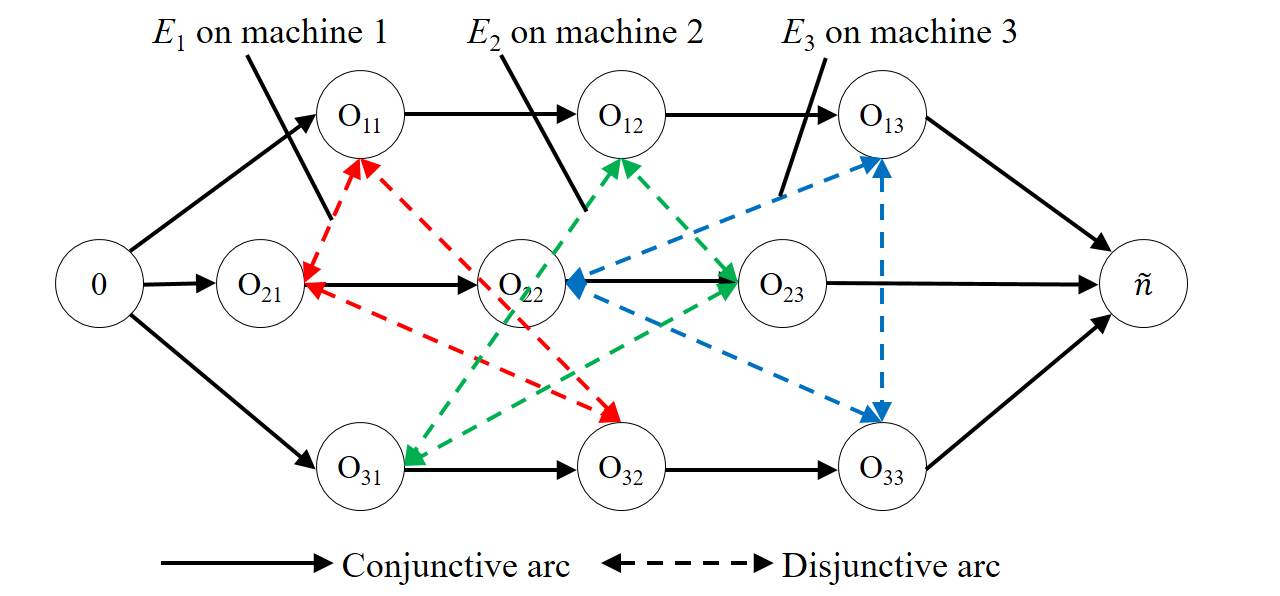
Job shop scheduling problem (JSP) is a widely studied NP-complete combinatorial optimization problem. Neighborhood structures play a critical role in solving JSP. At present, there are three state-of-the-art neighborhood structures, i.e., N5, N6, and N7. Improving the upper bounds of some famous benchmarks is inseparable from the role of these neighborhood structures. However, these existing neighborhood structures only consider the movement of critical operations within a critical block. According to our experiments, it is also possible to improve the makespan of a scheduling scheme by moving a critical operation outside its critical block. According to the above finding, this paper proposes a new N8 neighborhood structure considering the movement of critical operations within a critical block and the movement of critical operations outside the critical block. Besides, a neighborhood clipping method is designed to avoid invalid movement, reducing the computational time. Tabu search (TS) is a commonly used algorithm framework combined with neighborhood structures. This paper uses this framework to compare the N8 neighborhood structure with N5, N6, and N7 neighborhood structures on four famous benchmarks. The experimental results verify that the N8 neighborhood structure is more effective and efficient in solving JSP than the other state-of-the-art neighborhood structures.
翻译:工作坊时间安排问题(JSP)是一个广泛研究的全套组合优化问题。邻居结构在解决工作坊优化方面发挥着关键作用。目前,有三种最先进的邻里结构,即N5、N6和N7。改进一些著名基准的上限与这些邻里结构的作用密不可分。然而,这些现有邻里结构只考虑关键作业在关键街区内的流动情况。根据我们的实验,也可以通过将一个关键作业移到其关键街区之外来改进一个排期计划的范围。根据上述调查结果,本文件提出一个新的N8邻里结构,考虑关键作业在关键街区内的移动以及关键街区以外的关键作业的移动。此外,设计邻里剪切方法是为了避免无效的移动,减少计算时间。塔布搜索(TS)是一个常用的算法框架,它与邻里结构相结合。本文使用这个框架将N8邻里结构与N5、N6和N7邻里结构在四个著名的基准上加以比较。实验结果证实,N8邻里结构比JS-P更有效和高效地解决其他州JS-P的邻里结构。