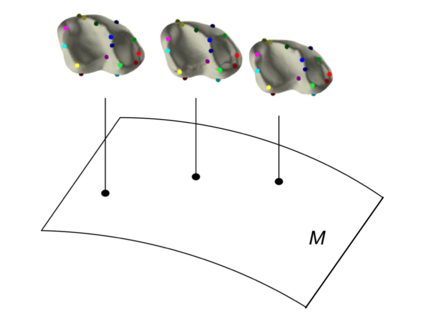
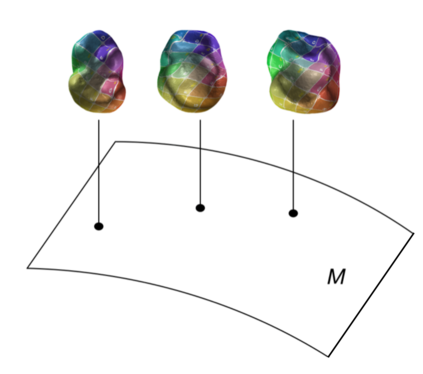
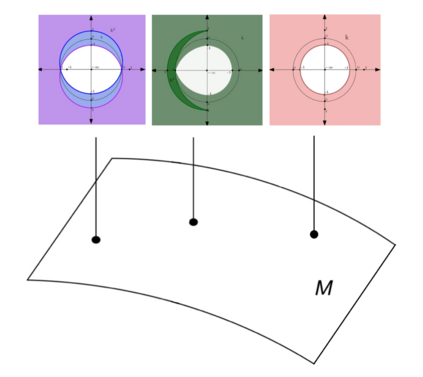
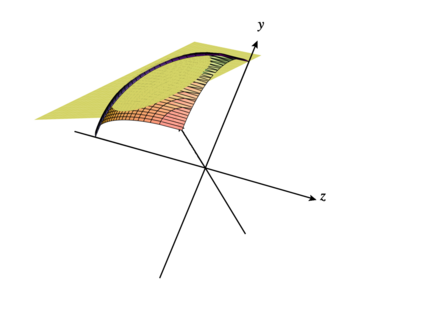
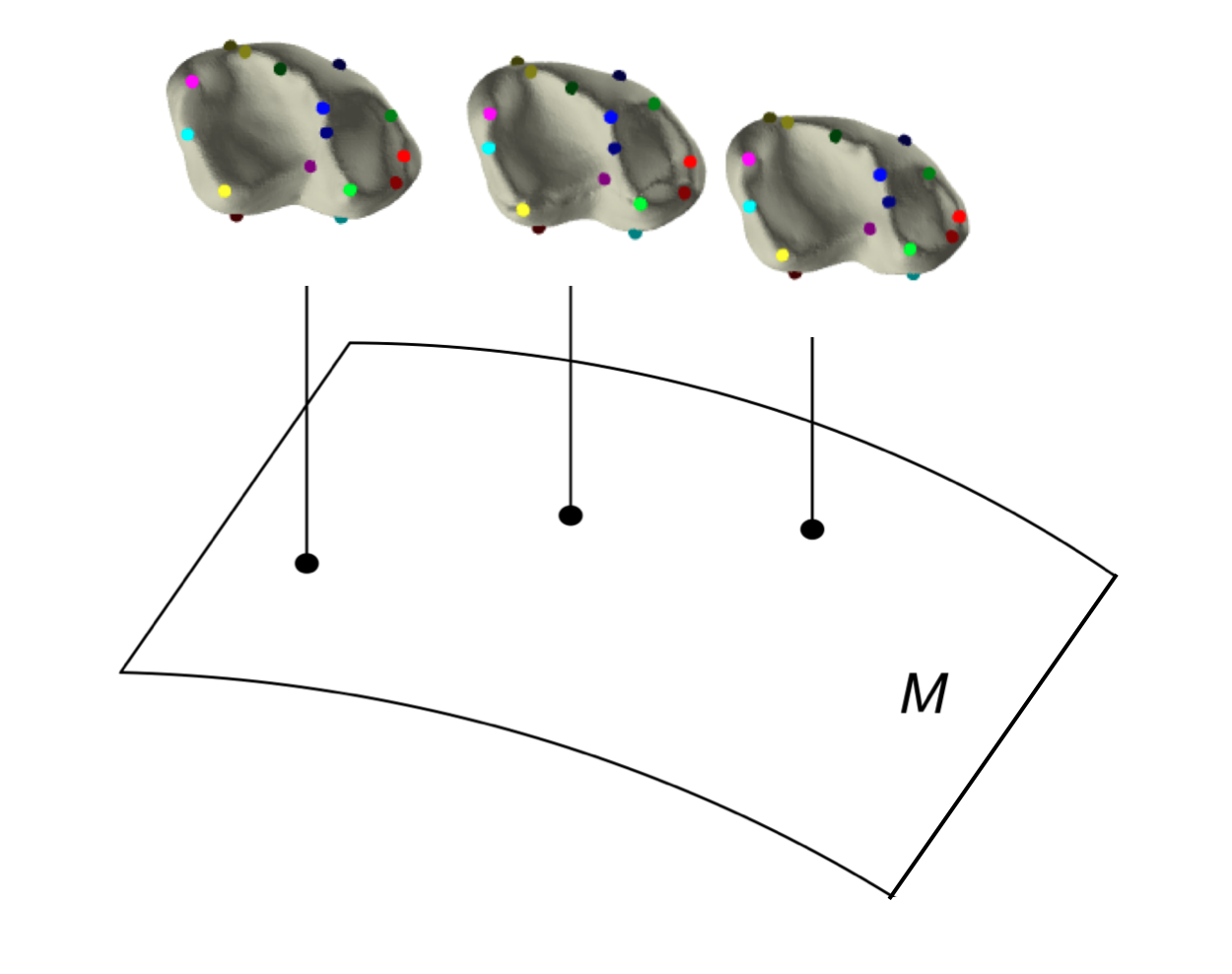
We present a sheaf-theoretic construction of shape space -- the space of all shapes. We do this by describing a homotopy sheaf on the poset category of constructible sets, where each set is mapped to its Persistent Homology Transform (PHT). Recent results that build on fundamental work of Schapira have shown that this transform is injective, thus making the PHT a good summary object for each shape. Our homotopy sheaf result allows us to "glue" PHTs of different shapes together to build up the PHT of a larger shape. In the case where our shape is a polyhedron we prove a generalized nerve lemma for the PHT. Finally, by re-examining the sampling result of Smale-Niyogi-Weinberger, we show that we can reliably approximate the PHT of a manifold by a polyhedron up to arbitrary precision.
翻译:我们展示了一个形状空间的沙夫理论构造, 即所有形状的空间。 我们通过描述一个在可建构组的外形类别上的同质结构。 每组都绘制成其持久性同族体变形( PHT ) 。 最近基于Schapira 基本工作的结果显示, 这种变形是注射性的, 从而使 PHT 成为每个形状的一个很好的摘要对象。 我们的同质结构变形让我们能够“ 凝聚” PHT 不同形状的PHT, 一起构建一个更大的形状的 PHT。 如果我们的形状是多面体, 我们证明对 PHT 来说是一种普遍的神经列心。 最后, 通过重新审查 Smal- Niyogi- Weinberger 的取样结果, 我们证明我们可以以任意精确的多面来可靠地接近多面形的 PHT 。