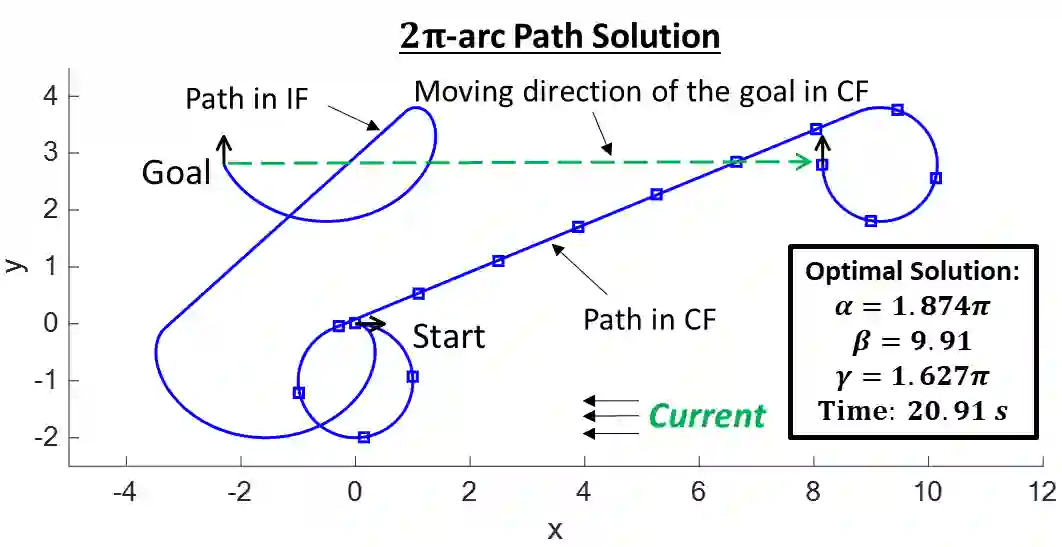
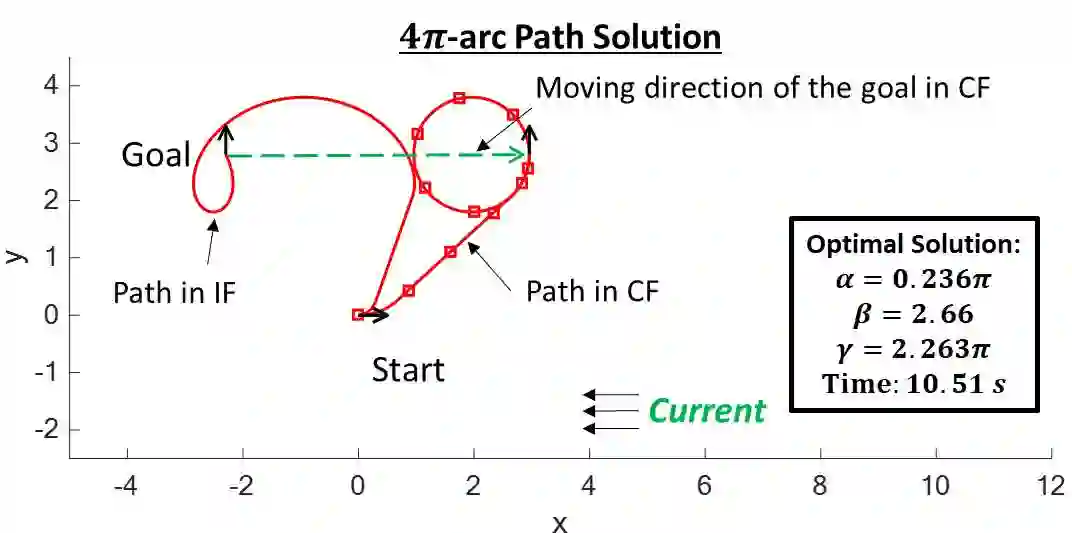
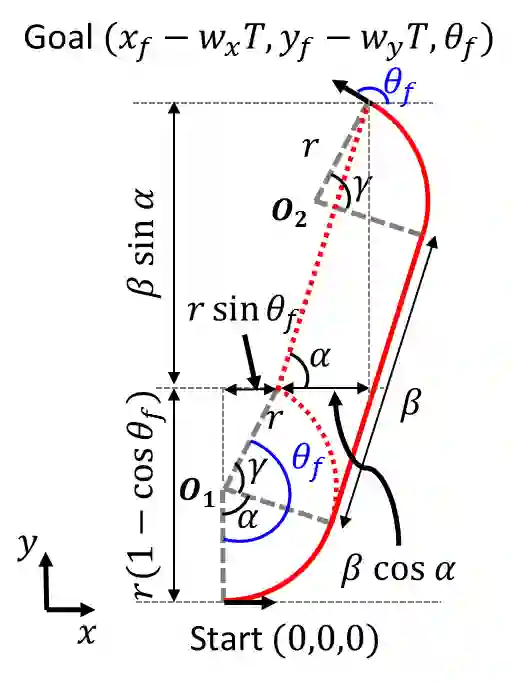
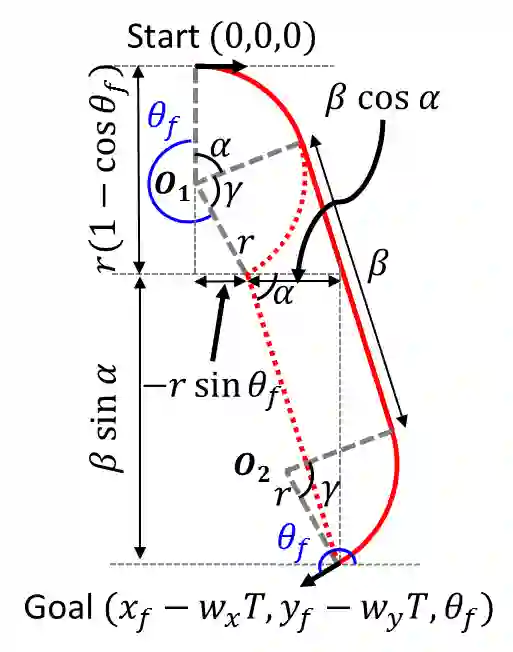
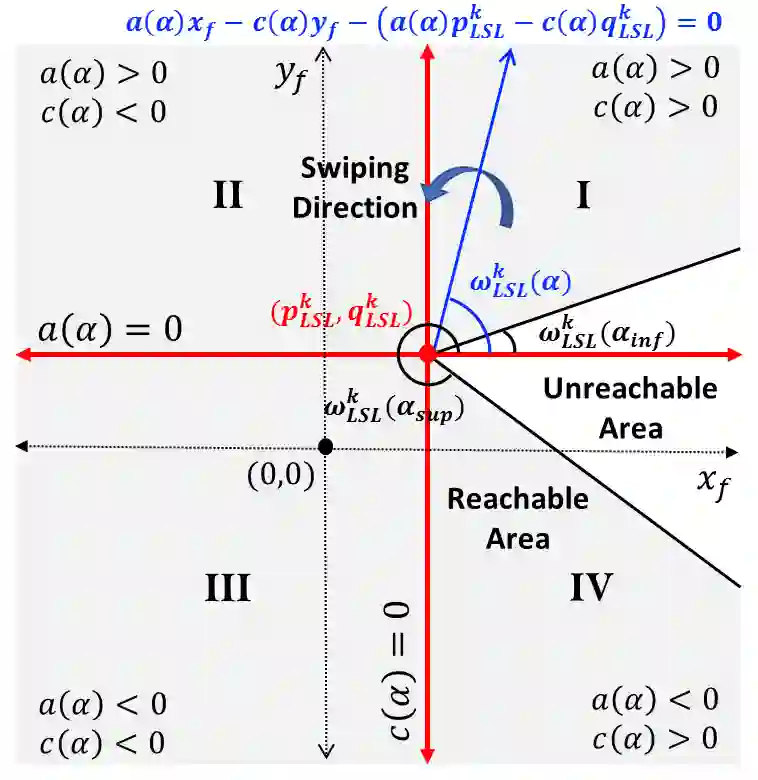
This paper presents a rapid (real time) solution to the minimum-time path planning problem for Dubins vehicles under environmental currents (wind or ocean currents). Real-time solutions are essential in time-critical situations (such as replanning under dynamically changing environments or tracking fast moving targets). Typically, Dubins problem requires to solve for six path types; however, due to the presence of currents, four of these path types require to solve the root-finding problem involving transcendental functions. Thus, the existing methods result in high computation times and their applicability for real-time applications is limited. In this regard, in order to obtain a real-time solution, this paper proposes a novel approach where only a subset of two Dubins path types (LSL and RSR) are used which have direct analytical solutions in the presence of currents. However, these two path types do not provide full reachability. We show that by extending the feasible range of circular arcs in the LSL and RSR path types from $2\pi$ to $4\pi$: 1) full reachability of any goal pose is guaranteed, and 2) paths with lower time costs as compared to the corresponding $2\pi$-arc paths can be produced. Theoretical properties are rigorously established, supported by several examples, and evaluated in comparison to the Dubins solutions by extensive Monte-Carlo simulations.
翻译:本文为Dubins车辆在环境潮流(风流或洋流)下的最低时间路程规划问题提供了一个快速(实时)的解决方案。实时解决方案在时间危急的情况下(如在动态变化的环境中重新规划或跟踪快速移动目标)至关重要。通常,Dubins问题需要解决6个路径类型;然而,由于流流的存在,其中4个路径类型需要解决涉及超常功能的根源调查问题。因此,现有方法导致高计算时间,其适用于实时应用的可能性有限。在这方面,为了获得实时解决方案,本文件建议采用新颖办法,即只使用两种Dubins路径类型(LSL和RSR)的子类(在动态变化环境中重新规划或跟踪快速移动目标)。通常,Dubins问题需要解决6个路径类型;然而,由于流流,这两种路径类型并不提供完全的可达到性。我们表明,通过将LSL和RSR路径中圆弧的可行范围从2\pi美元扩大到4\pi美元:1 任何目标组合的完全可实现性得到保证,2个途径,而采用较低时间成本的路径,在模拟模型中则以精确的轨道上支持。