Layer-wise Learning of Kernel Dependence Networks

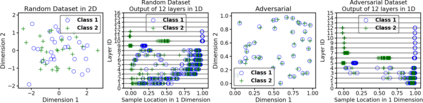
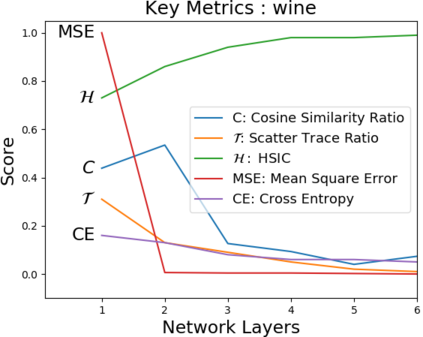
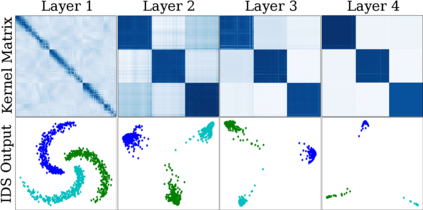
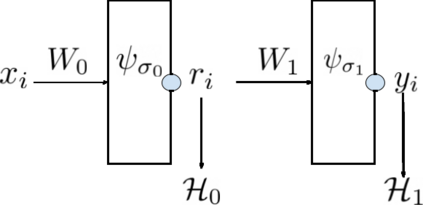
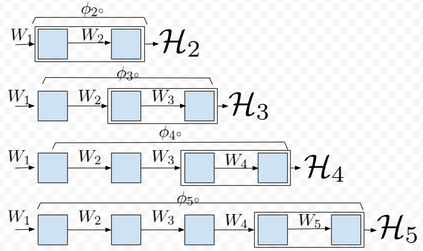
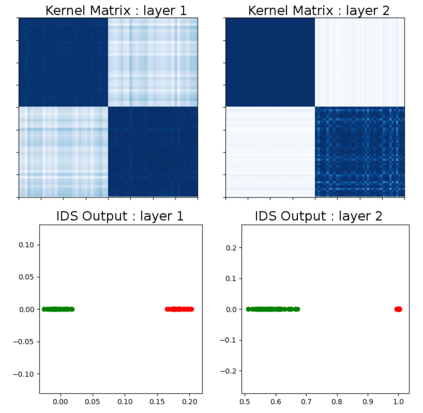
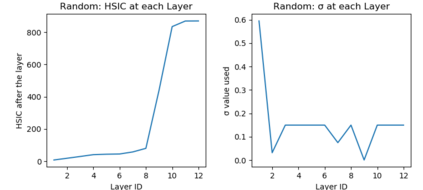
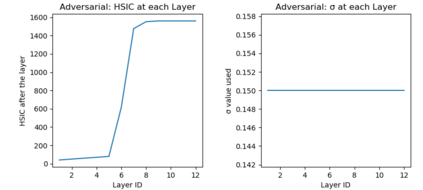
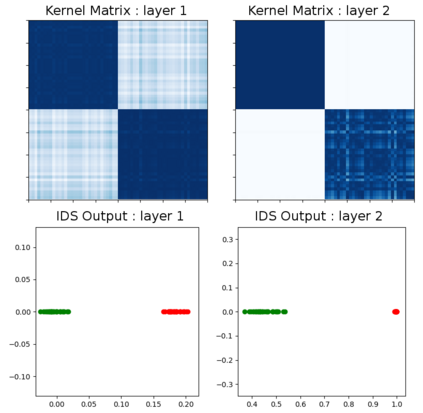
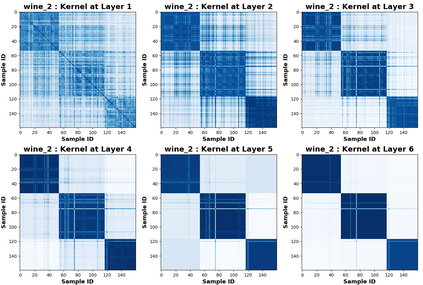
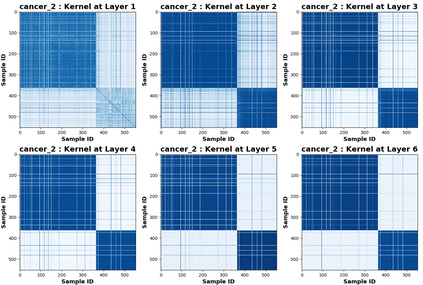
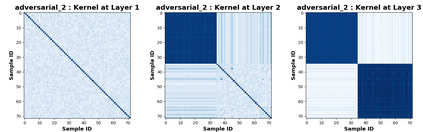
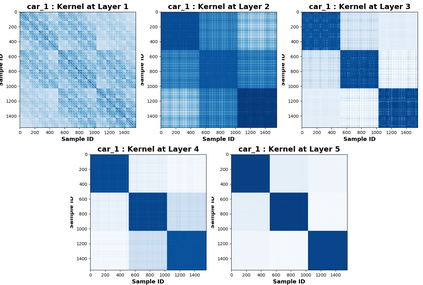
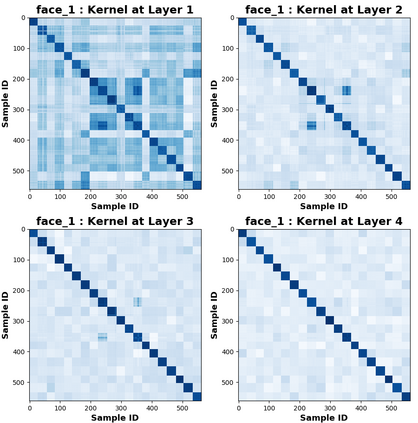
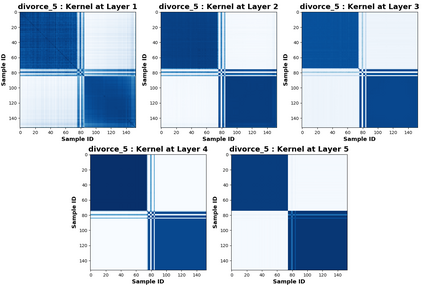
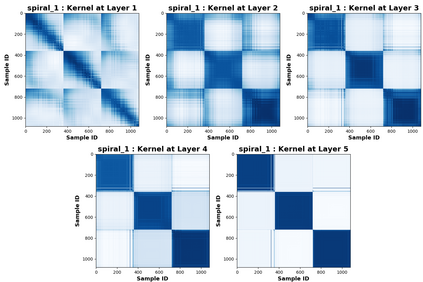
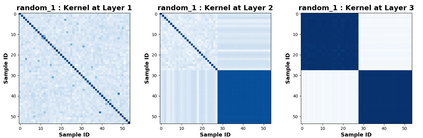
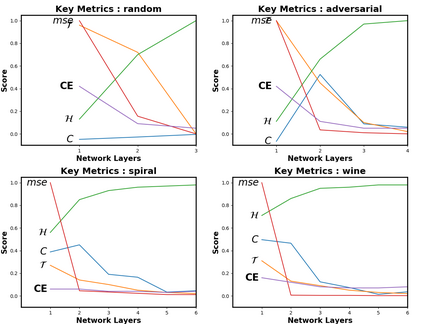
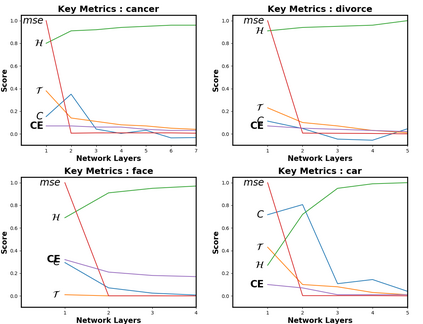
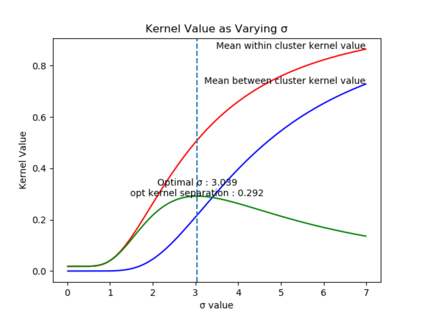
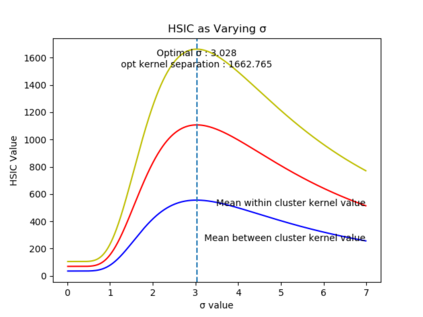
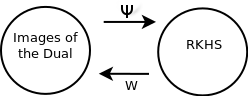
Due to recent debate over the biological plausibility of backpropagation (BP), finding an alternative network optimization strategy has become an active area of interest. We design a new type of kernel network, that is solved greedily, to theoretically answer several questions of interest. First, if BP is difficult to simulate in the brain, are there instead "trivial network weights" (requiring minimum computation) that allow a greedily trained network to classify any pattern. Perhaps a simple repetition of some basic rule can yield a network equally powerful as ones trained by BP with Stochastic Gradient Descent (SGD). Second, can a greedily trained network converge to a kernel? What kernel will it converge to? Third, is this trivial solution optimal? How is the optimal solution related to generalization? Lastly, can we theoretically identify the network width and depth without a grid search? We prove that the kernel embedding is the trivial solution that compels the greedy procedure to converge to a kernel with Universal property. Yet, this trivial solution is not even optimal. By obtaining the optimal solution spectrally, it provides insight into the generalization of the network while informing us of the network width and depth.