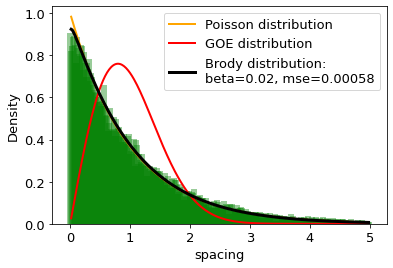
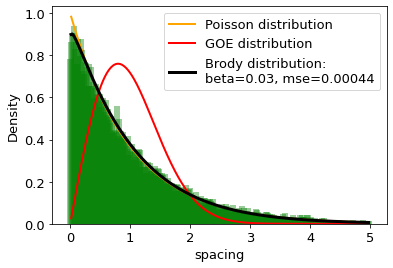
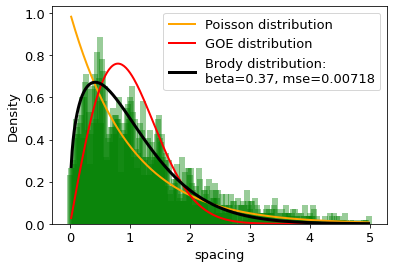
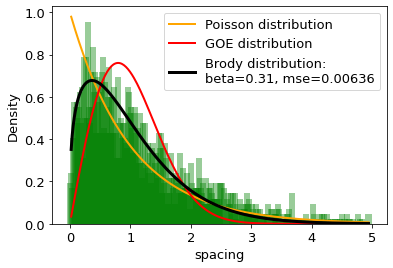
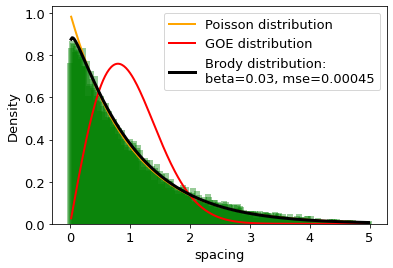
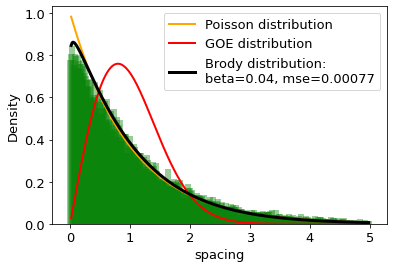
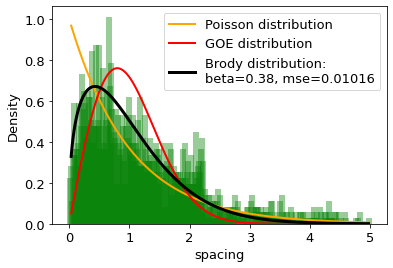
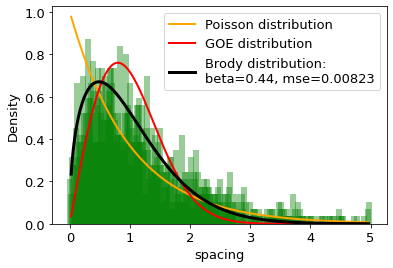
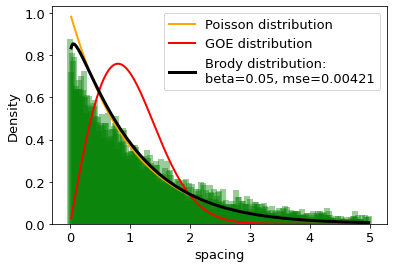
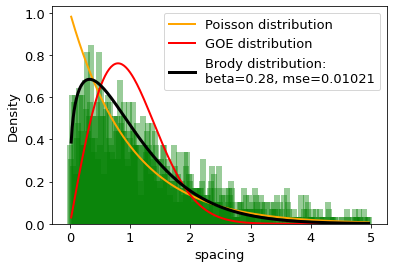
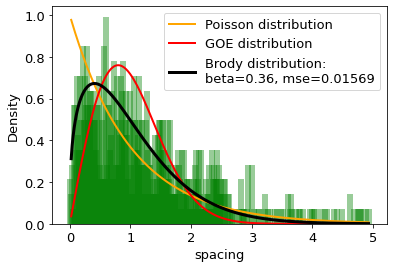
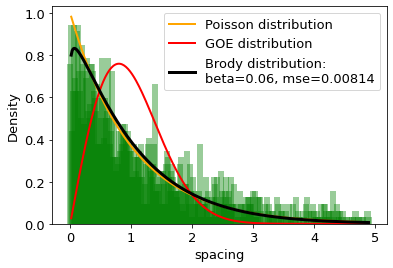
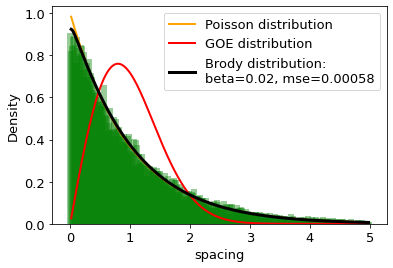
The distances between words calculated in word units are studied and compared with the distributions of the Random Matrix Theory (RMT). It is found that the distribution of distance between the same words can be well described by the single-parameter Brody distribution. Using the Brody distribution fit, we found that the distance between given words in a set of texts can show mixed dynamics, coexisting regular and chaotic regimes. It is found that distributions correctly fitted by the Brody distribution with a certain goodness of the fit threshold can be identifid as stop words, usually considered as the uninformative part of the text. By applying various threshold values for the goodness of fit, we can extract uninformative words from the texts under analysis to the desired extent. On this basis we formulate a fully agnostic recipe that can be used in the creation of a customized set of stop words for texts in any language based on words.
翻译:对用文字单位计算的单词之间的距离进行了研究,并与随机矩阵理论(RMT)的分布进行比较。 发现同一词之间的距离分布可以通过单一参数Brody分布来很好地描述。 使用Brody分布的合适方法,我们发现一组文本中给定的单词之间的距离可以显示混杂的动态, 并同时存在常规和混乱的制度。 人们发现, Brody 分布的正确配齐的适合阈值的分布可以被识别为句式词, 通常被视为文本中不具有信息规范的部分。 通过应用各种临界值, 我们就可以从所分析的文本中提取非信息化的单词, 从而达到预期的程度。 在此基础上, 我们制定了一种完全不可知的配方, 可以用来为基于文字的任何语言的文本创建一套定制的断字。