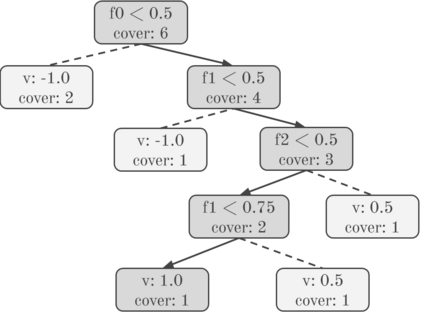
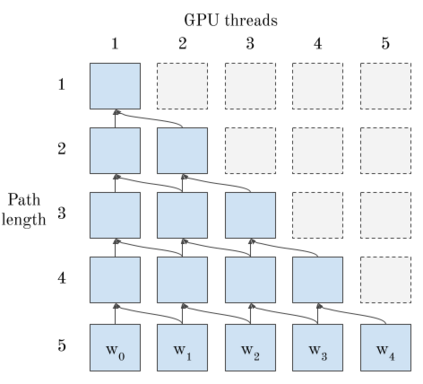
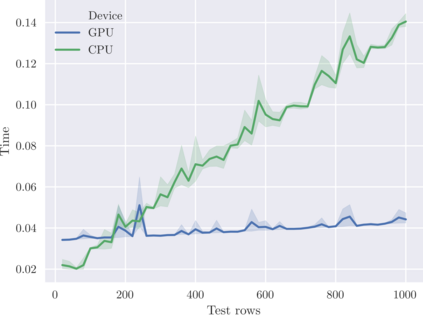
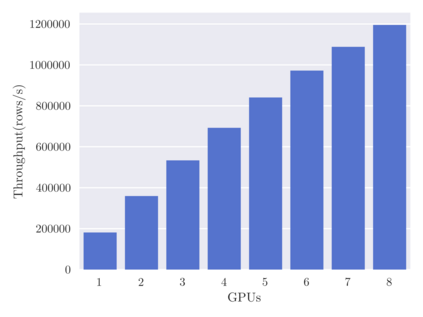
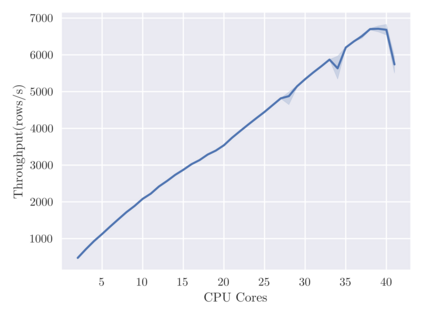
SHAP (SHapley Additive exPlanation) values provide a game theoretic interpretation of the predictions of machine learning models based on Shapley values. While exact calculation of SHAP values is computationally intractable in general, a recursive polynomial-time algorithm called TreeShap is available for decision tree models. However, despite its polynomial time complexity, TreeShap can become a significant bottleneck in practical machine learning pipelines when applied to large decision tree ensembles. Unfortunately, the complicated TreeShap algorithm is difficult to map to hardware accelerators such as GPUs. In this work, we present GPUTreeShap, a reformulated TreeShap algorithm suitable for massively parallel computation on graphics processing units. Our approach first preprocesses each decision tree to isolate variable sized sub-problems from the original recursive algorithm, then solves a bin packing problem, and finally maps sub-problems to single-instruction, multiple-thread (SIMT) tasks for parallel execution with specialised hardware instructions. With a single NVIDIA Tesla V100-32 GPU, we achieve speedups of up to 19x for SHAP values, and speedups of up to 340x for SHAP interaction values, over a state-of-the-art multi-core CPU implementation executed on two 20-core Xeon E5-2698 v4 2.2 GHz CPUs. We also experiment with multi-GPU computing using eight V100 GPUs, demonstrating throughput of 1.2M rows per second -- equivalent CPU-based performance is estimated to require 6850 CPU cores.
翻译:SHapley Additivie Explanation) 值提供了基于 Shapley 值的机器学习模型预测的游戏理论解释。 虽然精确计算 SHAP 值在总体上难以计算, 但是对于决策树模型来说, 有一种叫做 TreamShap 的递归性多边时间算法是可用的。 然而, 尽管它具有多元时间复杂性, 树Shap 在应用于大型决策树组时, 可以在实用机器学习管道中成为一个巨大的瓶颈。 不幸的是, 复杂的 TreShap 算法很难映射到 GPUs 等硬件加速器。 在这项工作中, 我们还展示了 GPSAP 的精确计算方法。 我们的方法首先将每个决定树从原始的递解算中分离可变大小的子分数, 然后解决一个 bin 包装问题, 最后将基于 equu- pual 的子方案, 多重读取 (SIMTMTH) 任务映射到 C- Exqual C- suples 的 C- sal deal developmental 20- cal exal exal deal ex a. gVIAx ex- hownx ax ax axxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx