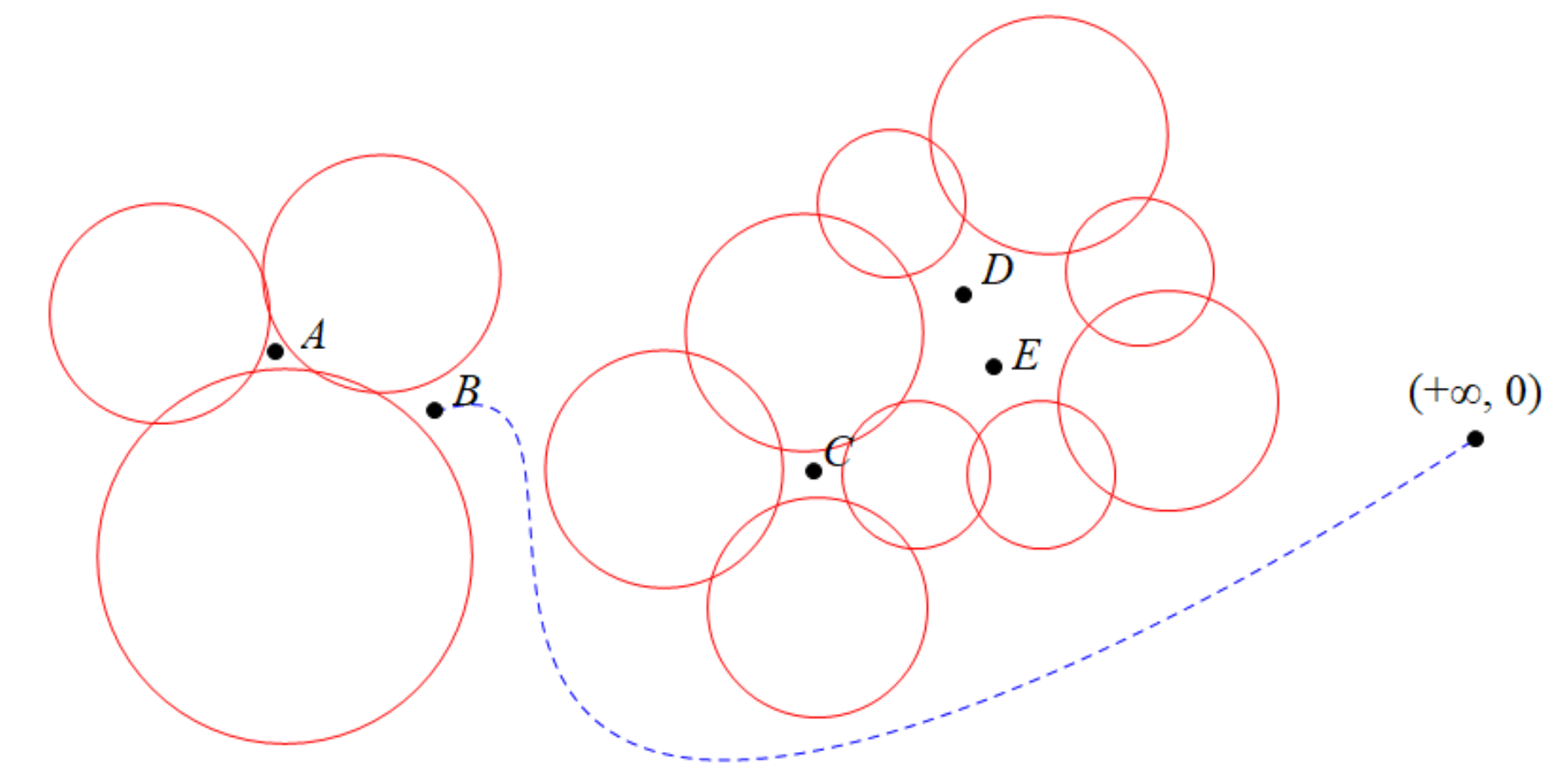
Let $X$ be a set of points in $\mathbb{R}^2$ and $\mathcal{O}$ be a set of geometric objects in $\mathbb{R}^2$, where $|X| + |\mathcal{O}| = n$. We study the problem of computing a minimum subset $\mathcal{O}^* \subseteq \mathcal{O}$ that encloses all points in $X$. Here a point $x \in X$ is enclosed by $\mathcal{O}^*$ if it lies in a bounded connected component of $\mathbb{R}^2 \backslash (\bigcup_{O \in \mathcal{O}^*} O)$. We propose two algorithmic frameworks to design polynomial-time approximation algorithms for the problem. The first framework is based on sparsification and min-cut, which results in $O(1)$-approximation algorithms for unit disks, unit squares, etc. The second framework is based on LP rounding, which results in an $O(\alpha(n)\log n)$-approximation algorithm for segments, where $\alpha(n)$ is the inverse Ackermann function, and an $O(\log n)$-approximation algorithm for disks.
翻译:暂无翻译