A combined volume penalization / selective frequency damping approach for immersed boundary methods applied to high-order schemes

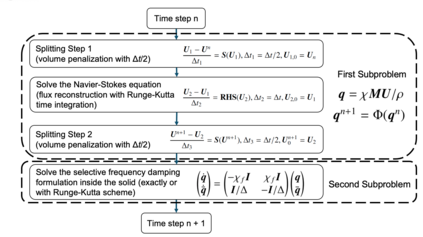
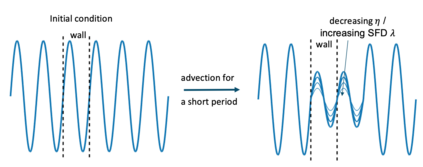
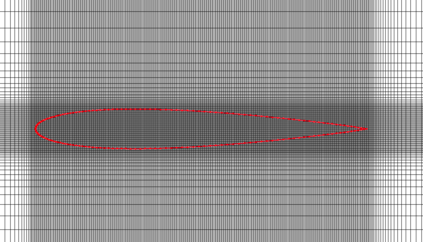
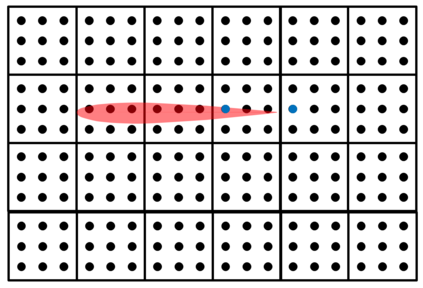
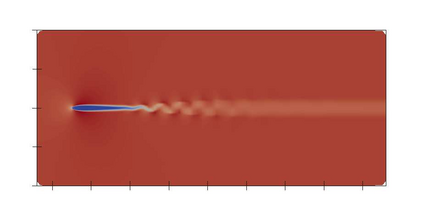
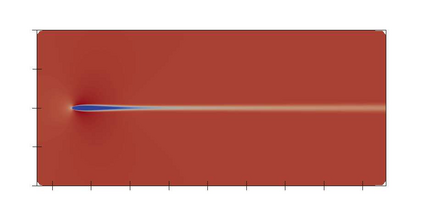
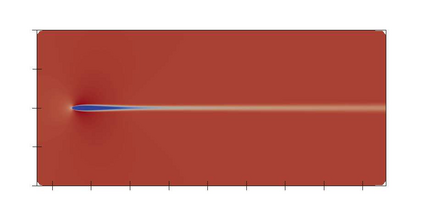
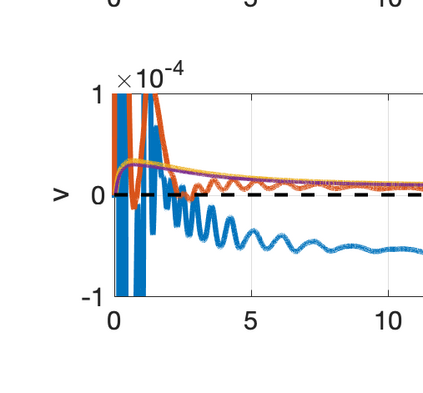
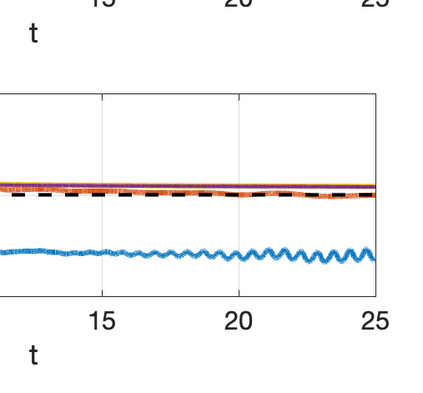
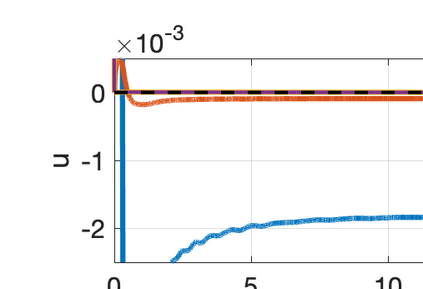
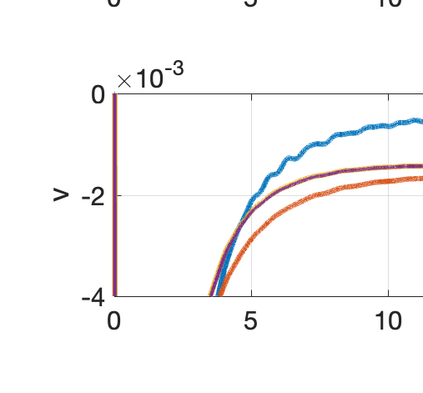
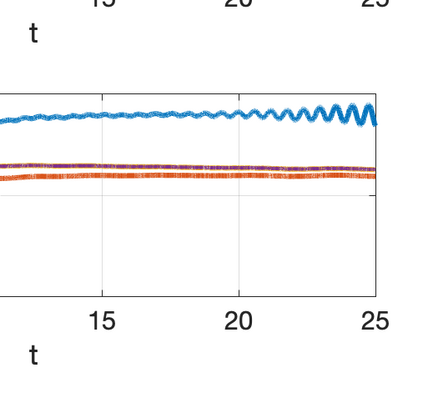
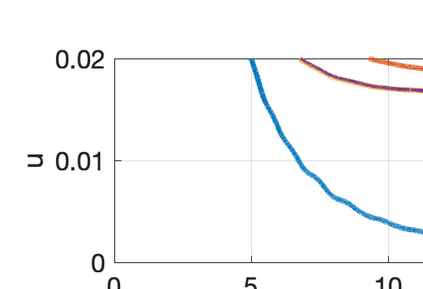
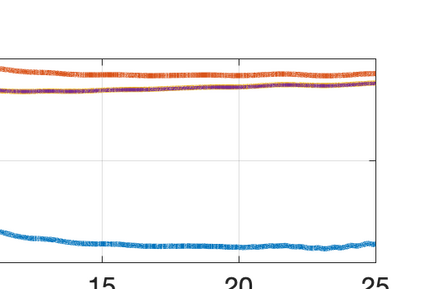
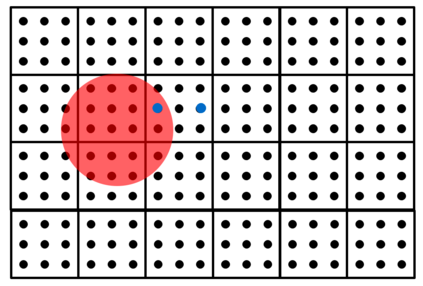
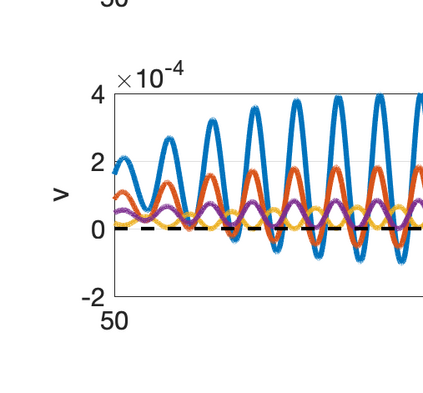
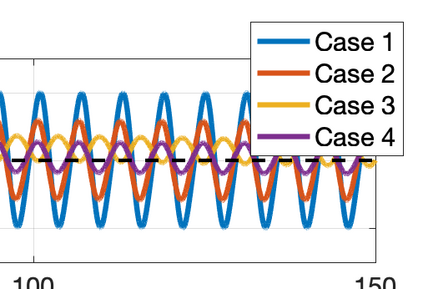
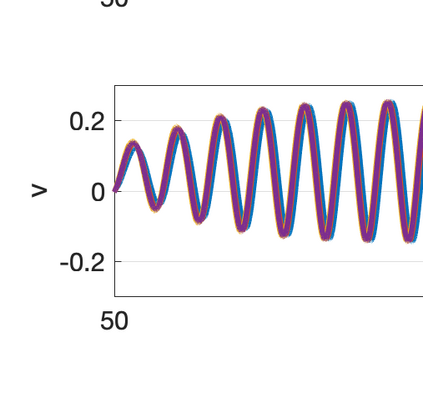
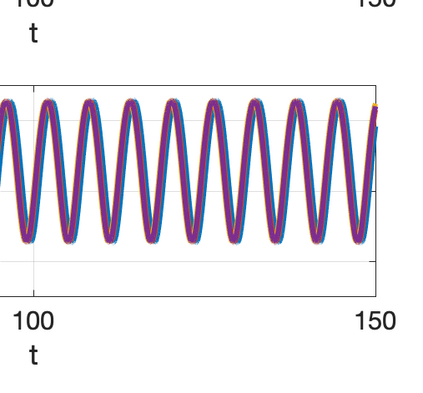
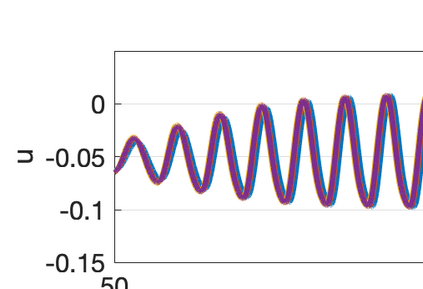
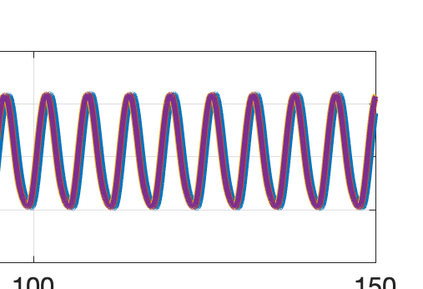
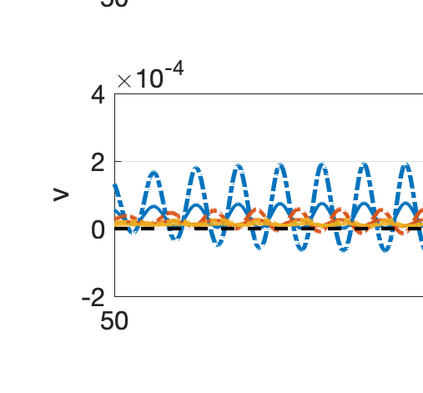
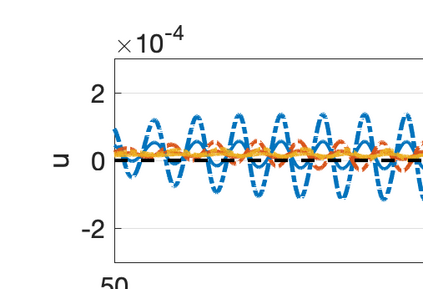
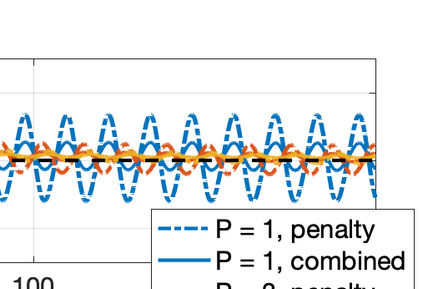
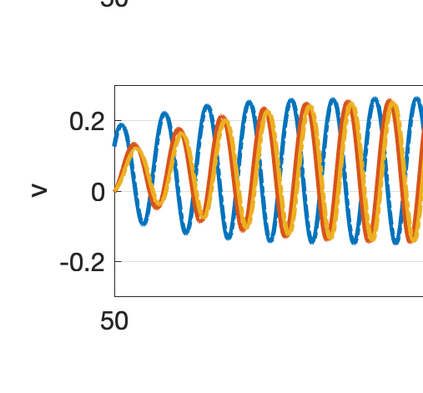
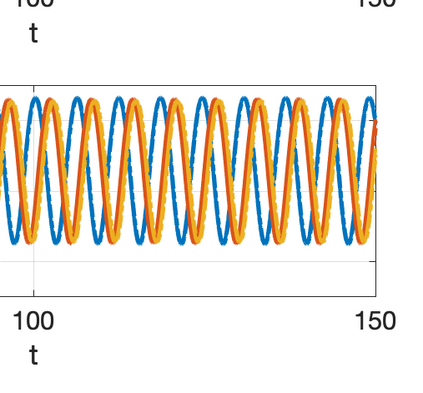
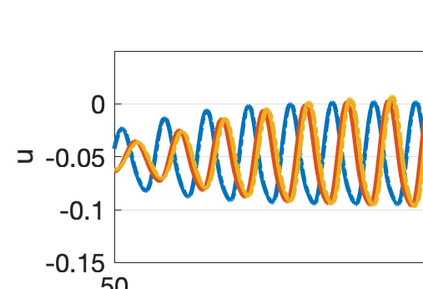
There has been an increasing interest in developing efficient immersed boundary method (IBM) based on Cartesian grids, recently in the context of high-order methods. IBM based on volume penalization is a robust and easy to implement method to avoid body-fitted meshes and has been recently adapted to high order discretisations (Kou et al., 2021). This work proposes an improvement over the classic penalty formulation for flux reconstruction high order solvers. We include a selective frequency damping (SFD) approach (Aakervik et al., 2006) acting only inside solid body defined through the immersed boundary masking, to damp spurious oscillations. An encapsulated formulation for the SFD method is implemented, which can be used as a wrapper around an existing time-stepping code. The numerical properties have been studied through eigensolution analysis based on the advection equation. These studies not only show the advantages of using the SFD method as an alternative of the traditional volume penalization, but also show the favorable properties of combining both approaches. This new approach is then applied to the Navier-Stokes equation to simulate steady flow past an airfoil and unsteady flow past a circular cylinder. The advantages of the SFD method in providing improved accuracy are reported.