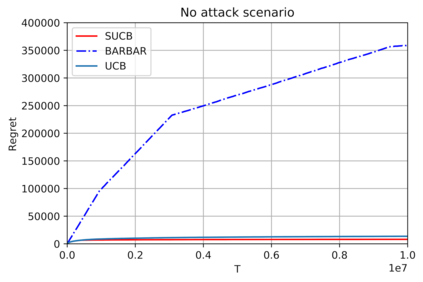
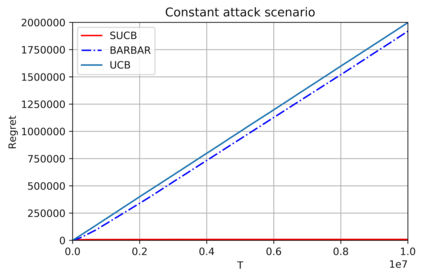
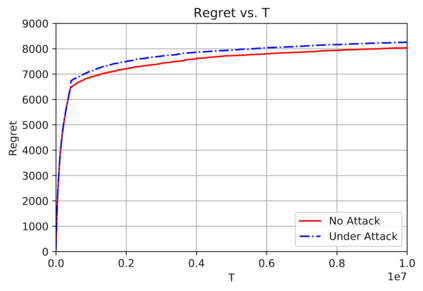
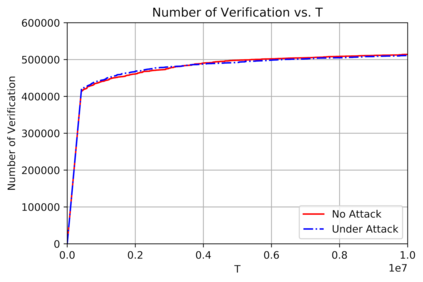
This paper studies bandit algorithms under data poisoning attacks in a bounded reward setting. We consider a strong attacker model in which the attacker can observe both the selected actions and their corresponding rewards, and can contaminate the rewards with additive noise. We show that \emph{any} bandit algorithm with regret $O(\log T)$ can be forced to suffer a regret $\Omega(T)$ with an expected amount of contamination $O(\log T)$. This amount of contamination is also necessary, as we prove that there exists an $O(\log T)$ regret bandit algorithm, specifically the classical UCB, that requires $\Omega(\log T)$ amount of contamination to suffer regret $\Omega(T)$. To combat such poising attacks, our second main contribution is to propose a novel algorithm, Secure-UCB, which uses limited \emph{verification} to access a limited number of uncontaminated rewards. We show that with $O(\log T)$ expected number of verifications, Secure-UCB can restore the order optimal $O(\log T)$ regret \emph{irrespective of the amount of contamination} used by the attacker. Finally, we prove that for any bandit algorithm, this number of verifications $O(\log T)$ is necessary to recover the order-optimal regret. We can then conclude that Secure-UCB is order-optimal in terms of both the expected regret and the expected number of verifications, and can save stochastic bandits from any data poisoning attack.
翻译:本文研究在受约束的奖赏环境下的数据中毒攻击中发生的土匪算法。 我们认为这是一个强大的攻击者模型, 攻击者可以在其中观察选定的行动及其相应的奖赏, 并且能够用添加噪音污染奖励。 我们显示, o(\logT) 的土匪算法, 可能被迫遭受遗憾 $\ omega( T) 美元, 预计污染数量有限 $O( log) T) 。 这种污染数量也是必要的, 因为我们证明有美元( log T) 的遗憾算法, 特别是古典 UCB, 需要美元(log T) 的污染数量来受遗憾 $\ Omega( T) 。 为了打击这种偷猎攻击, 我们的第二个主要贡献是提出一个新的算法, 安全( T), 使用有限的 eemph( T) 校验 。 我们用任何O(log T) 的预期数量, 安全- CUB 来恢复最理想的 ASLA 。