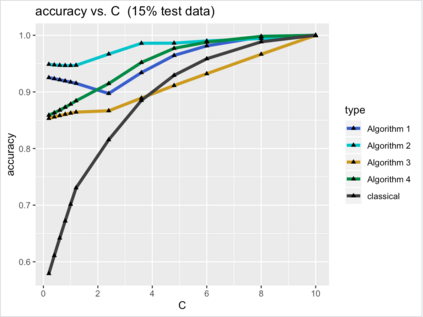
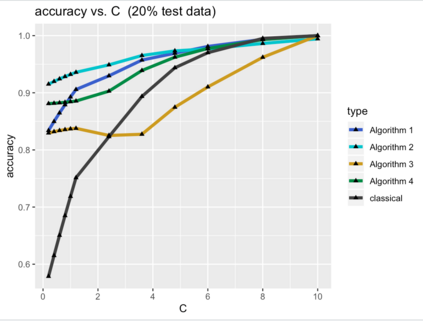
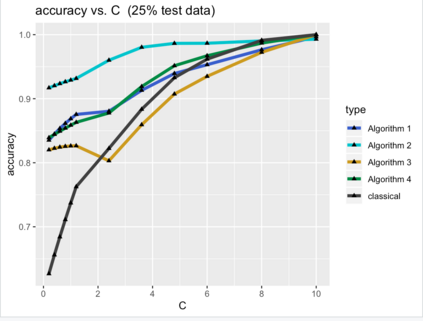
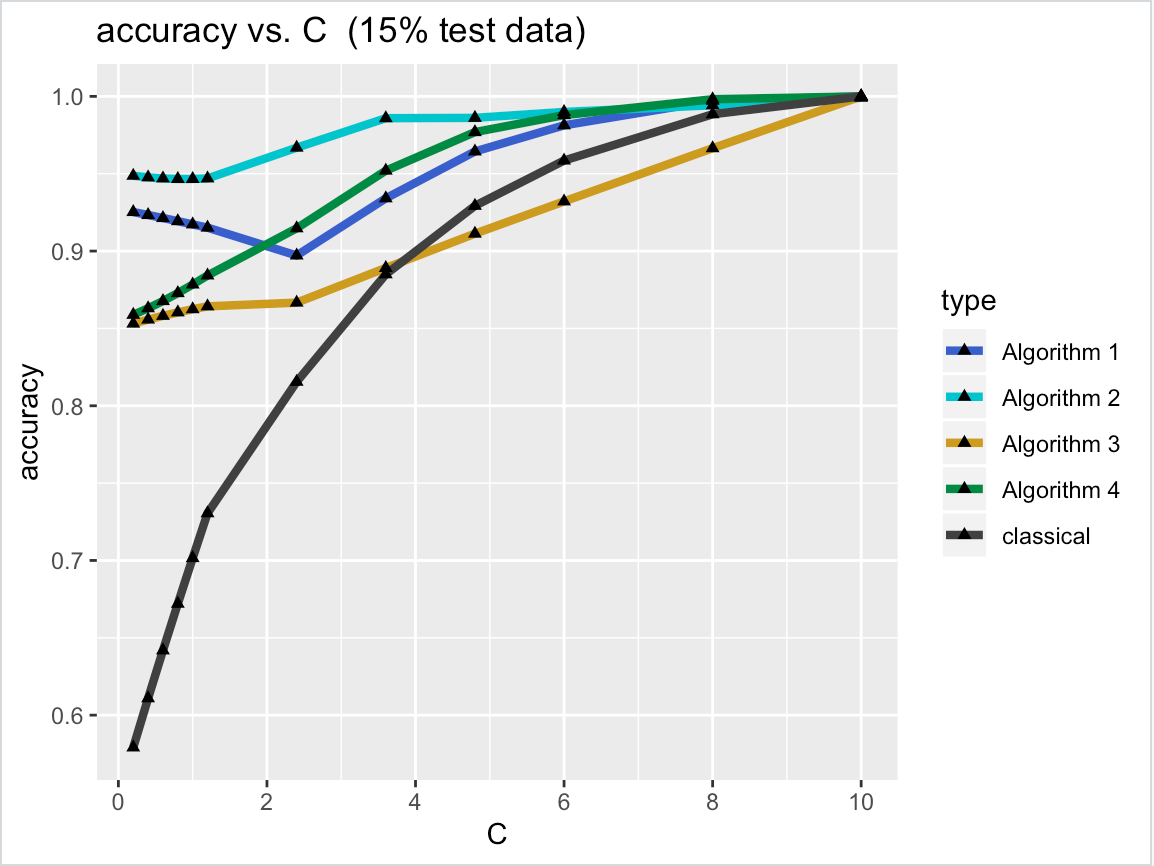
Most data in genome-wide phylogenetic analysis (phylogenomics) is essentially multidimensional, posing a major challenge to human comprehension and computational analysis. Also, we can not directly apply statistical learning models in data science to a set of phylogenetic trees since the space of phylogenetic trees is not Euclidean. In fact, the space of phylogenetic trees is a tropical Grassmannian in terms of max-plus algebra. Therefore, to classify multi-locus data sets for phylogenetic analysis, we propose tropical support vector machines (SVMs). Like classical SVMs, a tropical SVM is a discriminative classifier defined by the tropical hyperplane which maximizes the minimum tropical distance from data points to itself in order to separate these data points into sectors (half-spaces) in the tropical projective torus. Both hard margin tropical SVMs and soft margin tropical SVMs can be formulated as linear programming problems. We focus on classifying two categories of data, and we study a simpler case by assuming the data points from the same category ideally stay in the same sector of a tropical separating hyperplane. For hard margin tropical SVMs, we prove the necessary and sufficient conditions for two categories of data points to be separated, and we show an explicit formula for the optimal value of the feasible linear programming problem. For soft margin tropical SVMs, we develop novel methods to compute an optimal tropical separating hyperplane. Computational experiments show our methods work well. We end this paper with open problems.
翻译:基因组全部植物基因分析(植物基因组)中的大多数数据本质上是多层面的,对人体的理解和计算分析构成重大挑战。此外,我们不能直接将数据科学中的统计学习模型应用于一组植物基因树,因为植物基因树的空间不是Euclidean。事实上,植物基因树的空间是一个热带草原,在最大+代数方面,它是一个热带草原。因此,为了将多种热量数据集分类用于植物基因分析,我们建议热带支持矢量机器(SVMs)。像古典SVMs一样,热带SVM是一种由热带高平板所定义的有区别的分类方法,它能最大限度地增加从数据点到本身的数据点之间的最低限度热带遗传距离,以便将这些数据点分为热带预测区(半空间),从最硬的热带SVMs和较软边际的SVMmmmmm, 两者都可分为线性编程性编程问题。我们注重对两种数据的分类,我们研究一个比较简单的例子,将数据点从一个数据点从相同的软极值分为一个理想的极值分类, 显示我们所需要的热带模型的硬的极值。