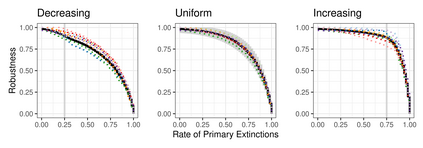
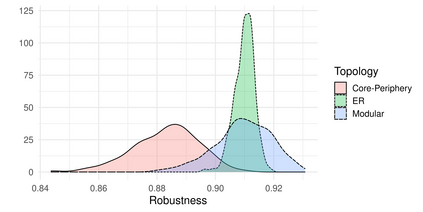
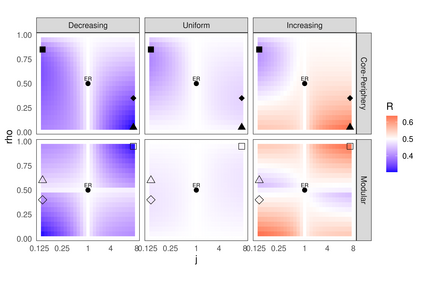
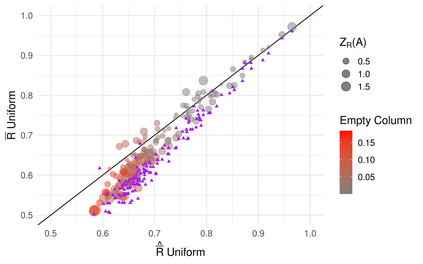
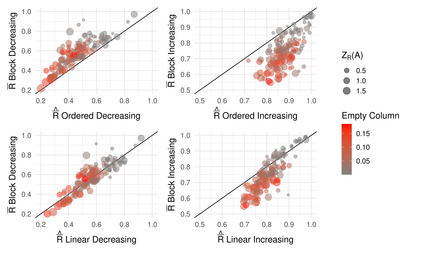
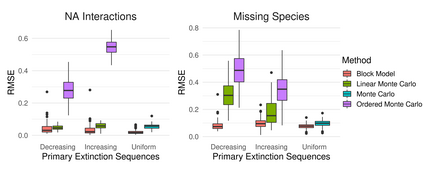
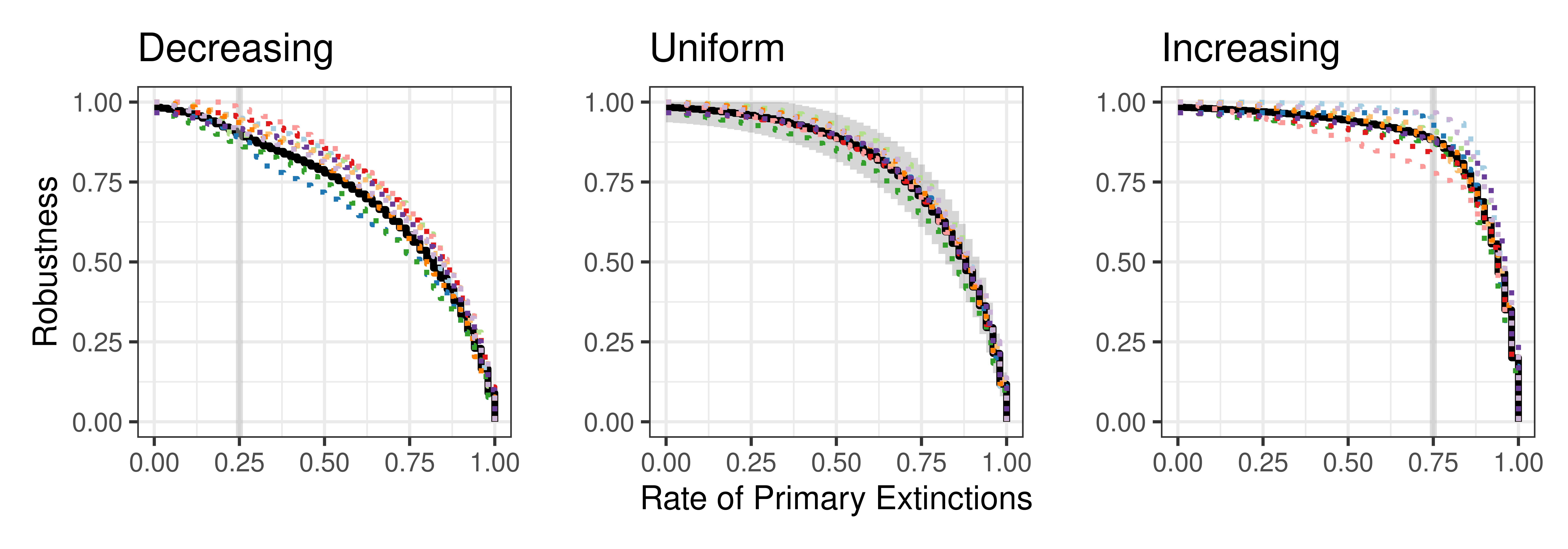
The robustness of an ecological network quantifies the resilience of the ecosystem it represents to species loss. It corresponds to the proportion of species that are disconnected from the rest of the network when extinctions occur sequentially. Classically, the robustness is calculated for a given network, from the simulation of a large number of extinction sequences. The link between network structure and robustness remains an open question. Setting a joint probabilistic model on the network and the extinction sequences allows to analyze this relation. Bipartite stochastic block models have proven their ability to model bipartite networks e.g. plant-pollinator networks: species are divided into blocks and interaction probabilities are determined by the blocks of membership. Analytical expressions of the expectation and variance of robustness are obtained under this model, for different distributions of primary extinction sequences. The impact of the network structure on the robustness is analyzed through a set of properties and numerical illustrations. The analysis of a collection of bipartite ecological networks allows us to compare the empirical approach to our probabilistic approach, and illustrates the relevance of the latter when it comes to computing the robustness of a partially observed or incompletely sampled network.
翻译:生态网络的坚固度是它代表的生态系统对物种流失的抗御力的量化。 它与物种在灭绝发生先后时与网络其他部分脱节的物种比例相对应。 典型地说, 从大量灭绝序列的模拟中计算出特定网络的坚固度。 网络结构和坚固度之间的联系仍是一个未决问题。 在网络和灭绝序列上设定一个联合概率模型,以便分析这一关系。 双部分分析区块模型已经证明它们有能力模拟双部分网络,例如植物-污染网络:物种被分成块块,互动概率由成员块决定。 在这个模型下,从主要灭绝序列的不同分布中,对强健性的期望和差异进行了分析。 网络结构对稳健性的影响通过一系列特性和数字图解进行分析。 对双部分生态网络的收集分析使我们得以比较经验方法与我们的概率方法,并表明后者在计算部分观测到或不完整的样本网络的稳健性时的相关性。