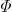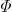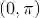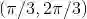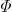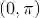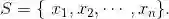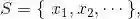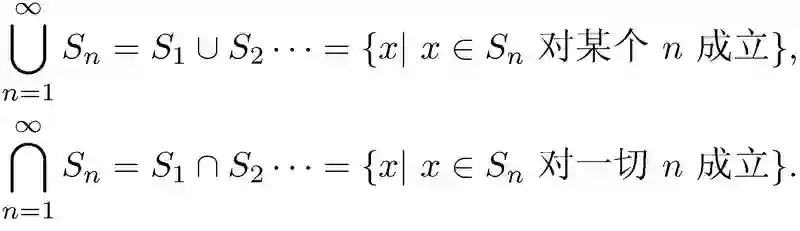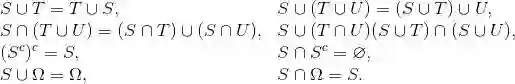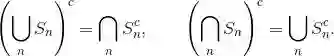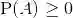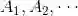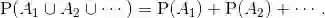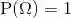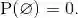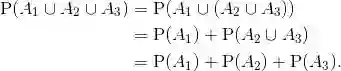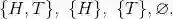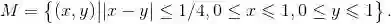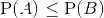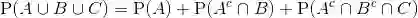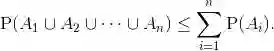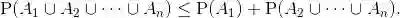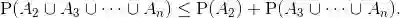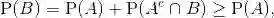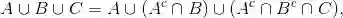样本空间与概率 | 《概率导论》

本文节选自《概率导论》（第2版·修订版）, 【遇见数学】已获授权！这里也特意推荐下，此书从直观、自然的角度阐述概率，是理工科学生入门首选之一概率书籍。

“概率”是一个非常有用的概念,它可以从不同的层面来加以解释.先看下面一幅对话场景.

一个病人被送进医院,并施以一种急救的药.病人家属为了了解药的疗效,询问了当班的护士.下面是他们之间的一段对话.

家属：护士小姐,请问这种药有效的概率是多少?

护士：我希望这种药是有效的,明天就会见分晓.

家属：是的,但是我想知道这种药有效的概率.

护士：每个病人的病情是不一样的,看情况发展吧.

家属：这么说吧,在100宗类似的病例中,你认为有多少宗是有效的?

护士(有些不耐烦)：我已经告诉你了,每个病人的情况是不一样的.这种药,对某些病人是有效的,对另一些病人是无效的.

家属(继续坚持)：现在请告诉我,如果必须打赌的话,你会押哪一注,这种药是有效还是无效?

护士(有些惊奇)：那我愿意打赌,对于这位病人,这种药是有效的.

家属(多少松了一口气)：好吧！我再问你,你是否愿意如此押注：若这药无效,你输掉2元钱;若这药有效,你赢1元钱?

护士(有些恼怒)：多么荒谬的想法！你是在浪费我的时间.

在这组对话中,病人家属希望用概率的概念同护士讨论药的疗效这种具有不确定性的事件.但是护士的第一反应是对概率这个概念的不认可,或不理解,而家属试图将概率的概念解释得更具体一些.他首先试图将概率解释成偶然事件在多次重复试验中出现的频率,这是最通常的解释.例如,我们说一枚两面对称的硬币,在抛掷试验中以50%的概率出现正面,这么说实际上是指在多次重复抛掷硬币时,出现正面向上的次数约占一半.但是护士似乎不大愿意接受家属的这种想法,护士的想法不是完全没有道理.如果这种药是第一次在医院里使用,或护士从没有过这方面的经验,那何从谈起治愈的频率呢?

在许多涉及不确定性的事例中,用频率解释是适宜的,然而,也有一些事例不宜用频率解释.比如,有一个学者以90%的把握断言《伊里亚特》和《奥德赛》是由同一作者创作的.由于他所讨论的是不可重复的一次性事件,这样的结论只是提供一些主观看法,而与频率无关.所谓概率为90%的把握只是学者的主观信念.或许有人认为主观信念是不值得研究的,至少从数学或科学的观点来看是如此.但是在实际生活中,人们面对不确定性的时候,经常不得不作出抉择.为了作出正确的或至少保持一致的抉择,科学和系统地利用他们的主观信念是一个先决条件.

事实上,一个理智的选择和行动揭示了许多内在的主观概率,然而在许多场合中,作出抉择的人自己也没有意识到他们应用了概率推理.在前面的对话场景中,病人家属以一种隐蔽的方式试图推断护士的主观信念.由于护士愿意以1:1的赔率打赌这种药是有效的,那么在护士的主观概念中,这种药有效的概率至少为50%.如果这位护士接受对话最后提出的赔率为2:1的赌注的话,这说明在护士的主观概念中,这种药有效的概率至少为2/3.

在此我们不去深究概率推理适用性方面的哲学问题,而是事先假定概率论在很多方面都具有实用价值,包括概率只反映主观信念的情形.概率论在科学、工程、医药、管理等领域中有许多成功应用的事例.这许多经验证据说明概率论在应用中是一种极其有用的工具.

本书的主要目的是发掘用概率模型描述不确定性的艺术和提高概率推理的能力.作为第一步,本章要把概率模型的基础结构及基本性质刻画清楚.概率是定义在某些试验结果的集合上的.为此,我们首先应该对集合论作一简介.

概率导论 第2版·修订版

作者：[美]伯特瑟卡斯（Dimitri P.Bertsekas），[美]齐齐克利斯（J

当当 广告

购买

1.1　集合

概率论大量应用集合运算.我们首先引进相关的记号和术语.

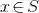
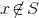
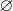
将一些研究对象放在一起,形成集合,而这些对象就称为集合的元素.设 S 是一个集合,x 是 S 的元素,我们将元素和集合的这种关系写成 .若 x 不是 S 的元素,就写成 .一个集合可以没有元素,这个特殊的集合就称为空集,记作 .

可用不同的方法刻画一个集合.若 S 包含有限个元素 ,我们只需将这些元素列在花括弧中：

例如,掷一枚骰子以后的所有可能结果的集合是{1,2,3,4,5,6},抛一枚硬币的可能结果的集合是{H,T },其中 H 代表正面向上,T 代表反面向上.

若 S 包含无限多个元素 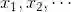,但它们可以像正整数那样排成一列,我们可写成

此时称 S 为可数无限集.例如,偶数的集合 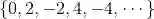 是一个可数无限集.

我们也可以以 x 具有某种性质 P 为条件来刻画一个集合,记作

{x |x 满足性质 P }.

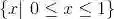
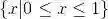
例如,偶数集合可写成{k |k/2 是整数}.类似地,在实数区间[0,1]中的数集可表示成 .注意,集合  是一个连续集合,它不可能排成一列(章后习题中给出了证明概要).这样的集合是不可数的集合.

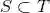
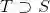
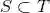
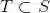
若集合 S 的所有元素均为集合 T 的元素,就称 S 为 T 的子集,记作  或 .若  且 ,则两个集合相等,记作S = T .引入空间的概念是十分必要的.将我们感兴趣的所有元素放在一起,形成一个集合,这个集合称为空间,记作 Ω.当 Ω 确定以后,我们所讨论的集合 S 都是 Ω 的子集.

1.1.1　集合运算

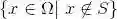
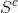
集合  称为集合 S 相对于 Ω 的补集,记作 .注意 .

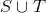
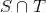
由属于 S 或属于 T 的元素组成的集合称为 S 和 T 的并,记为 .既属于 S 又属于 T 的元素组成的集合称为 S 和 T 的交,记成 .这些集合可用下列公式表达:

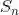
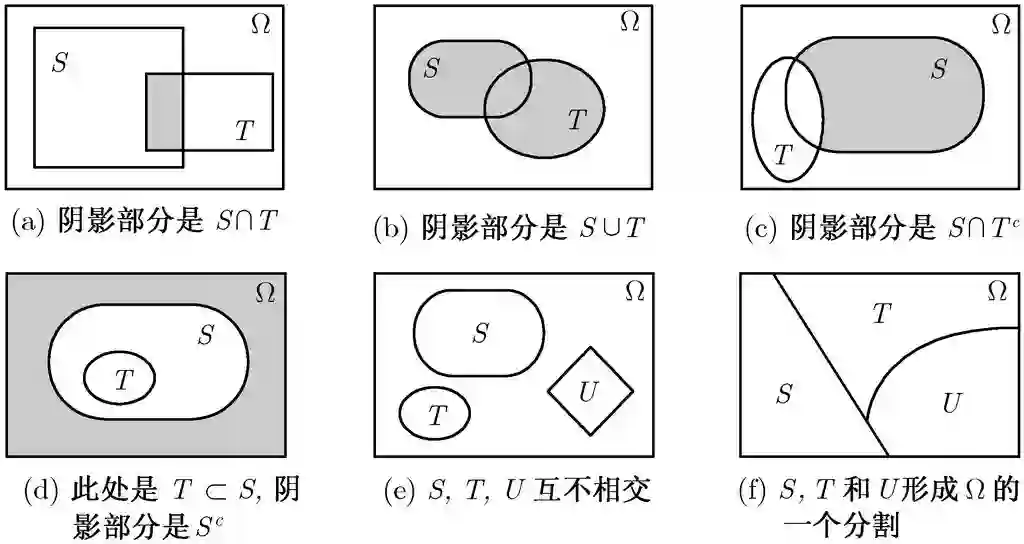
有时候我们需要考虑几个甚至无穷个集合的并和交的问题.例如,如果每一个正整数 n 都确定一个集合 ,则

图 1.1　维恩图的例子

两个集合称为不相交的,如果它们的交集为空集.更一般地,几个集合称为互不相交的,如果任何两个集合没有公共元素.一组集合称为集合 S 的分割,如果这组集合中的集合互不相交,并且它们的并为 S.

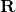
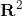
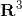
设 x 和 y 为两个研究对象,我们用(x,y)表示 x 和 y 的有序对.我们用  表示实数集合,用  表示实数对的集合,即二维平面,用 表示三维实数向量的集合(三维空间).集合及其运算可用维恩图形象化表示,见图1.1.

1.1.2　集合的代数

集合运算具有若干性质,这些运算性质可由运算的定义直接证得,举例如下：

下面给出的两个公式就是著名的德摩根定律：

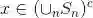
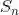
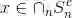
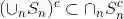
现在证明第一个公式.设 ,这说明 ,即对一切 n,.因而,对每一个 n,x 属于  的补集,即 .这样,我们得到 .反过来包含关系的证明,只需将我们的论证从后面往前推即可.而第二个公式的证明完全类似.

1.2　概率模型

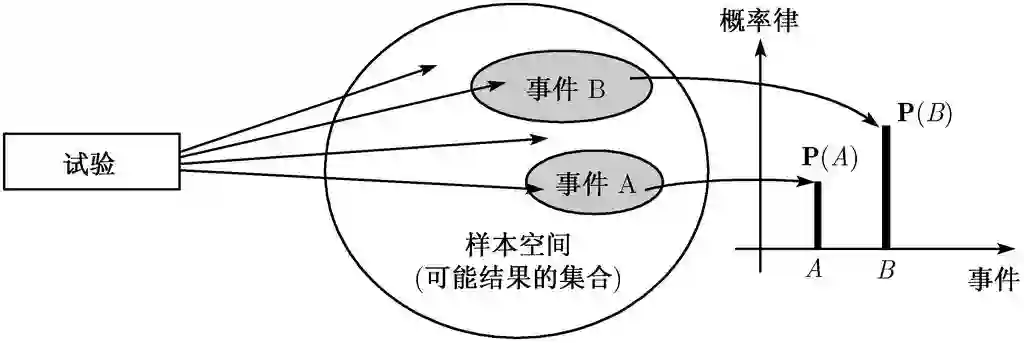
概率模型是对不确定现象的数学描述.为了与本节讨论的基本框架保持一致,下面列出了它的两个基本构成,并用图1.2做了形象阐释.

概率模型的基本构成

• 样本空间 ,这是一个试验的所有可能结果的集合.

• 概率律,概率律为试验结果的集合 A(称为事件)确定一个非负数P(A)(称为事件 A 的概率).而这个非负数刻画了我们对事件 A 的认识或所产生的信念的程度.稍后将指出概率律必须满足的某些性质.

图 1.2　概率模型的基本构成

1.2.1　样本空间和事件

每一个概率模型都关联着一个试验,这个试验将产生一个试验结果.该试验的所有可能结果形成样本空间,用 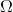 表示样本空间.样本空间的子集,即某些试验结果的集合,称为事件1.一个试验由什么组成,并没有什么限制.例如,可以抛掷一次硬币,也可以抛掷三次硬币,或持续地、无限次地抛掷硬币.然而我们所讨论的概率模型的问题中,只涉及一个试验.所以连续抛掷三次硬币的试验,只能作为一次试验,不能认为是三次试验.

1任意一个可能结果的集合,包括样本空间  本身和它的补集 ,都可能作为事件.当然,严格来讲,在一个具有不可数无限多个试验结果的样本空间中,有些子集不可能定义有意义的概率.这涉及测度论的数学知识.但实际上我们一般不会遇到这种特殊的情况,因此我们不必考虑这种特殊问题.

样本空间可由若干个试验结果组成,也可由无限多个试验结果组成.从数学上和概念上来看,有限样本空间比较简单.实际应用中,具有无限多个结果的样本空间也是很常见的.例如,往一个方形目标上掷飞标,可将每个可能的弹着点作为试验的结果.

1.2.2　选择适当的样本空间

在确定样本空间的时候,不同的试验结果必须是相互排斥的,这样,在试验过程中只可能产生唯一的一个结果.例如,当试验是掷一枚骰子的时候,不能把“1 或 3”定为一个试验结果,同时又把“1 或 4”也定义为一个结果.如果这样定义了,那么当掷得1点的时候,就不知道得到的是什么结果了.

对同一个试验,根据我们的兴趣可以确定不同模型.但是确定模型时,我们不能遗漏其样本空间中的任何一个结果.也就是说在试验过程中不管发生什么情况,我们总能够得到样本空间中的一个结果.另外,在建立样本空间的时候,要有足够的细节区分我们感兴趣的事件,同时要避免不必要的烦琐.

例 1.1　考虑两个不同的游戏,它们都涉及连续抛掷10次硬币.

游戏1：每次抛掷硬币的时候,只要出现正面向上,我们就赢1元钱.

游戏2：每次抛掷硬币时,我们都赢1元钱,直到出现第一次正面向上(包括这一次).以后每次抛掷硬币时我们赢2元钱,一直到第二次出现正面向上.每次抛掷得到正面向上的时候,以后每次抛掷硬币所赢的钱数比以前每次抛掷硬币所赢得的钱数加倍.

在游戏1中,我们赢的钱数只与10次抛掷中正面向上的次数有关;而在游戏2中,我们的赢钱数不仅与正面出现的次数有关,也与正反面出现的顺序有关.这样在游戏1中,样本空间可由11个(即 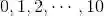 )试验结果组成,而在游戏2中,样本空间由所有的长度为10的正、反序列组成.

1.2.3　序贯模型

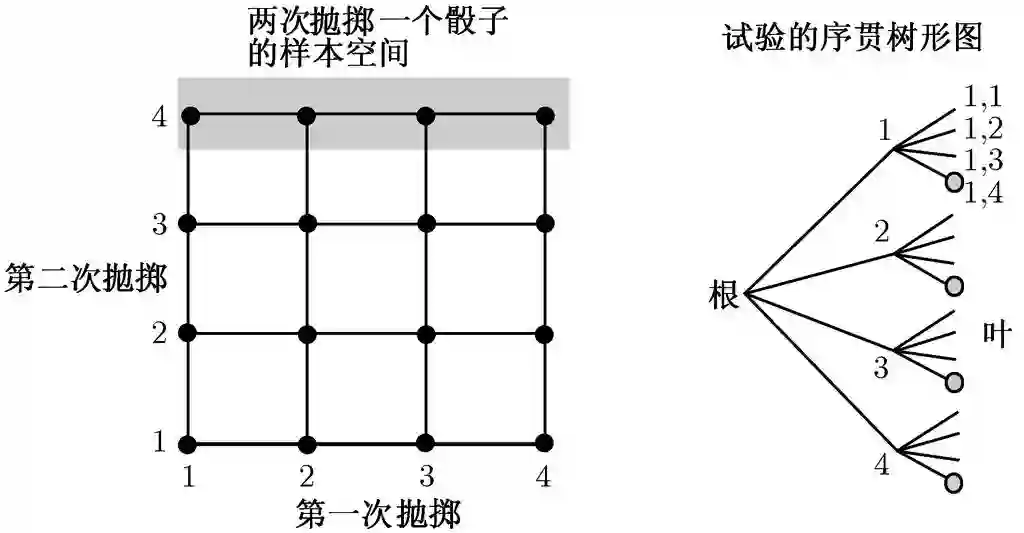
许多试验本身具有序贯的特征.例如,连续抛掷一枚硬币,一共抛三次,或者连续观察一只股票,共观察5天,又或者在一个通信接收设备上接收8位数字.常用序贯树形图来刻画样本空间中的试验结果,如图1.3所示.

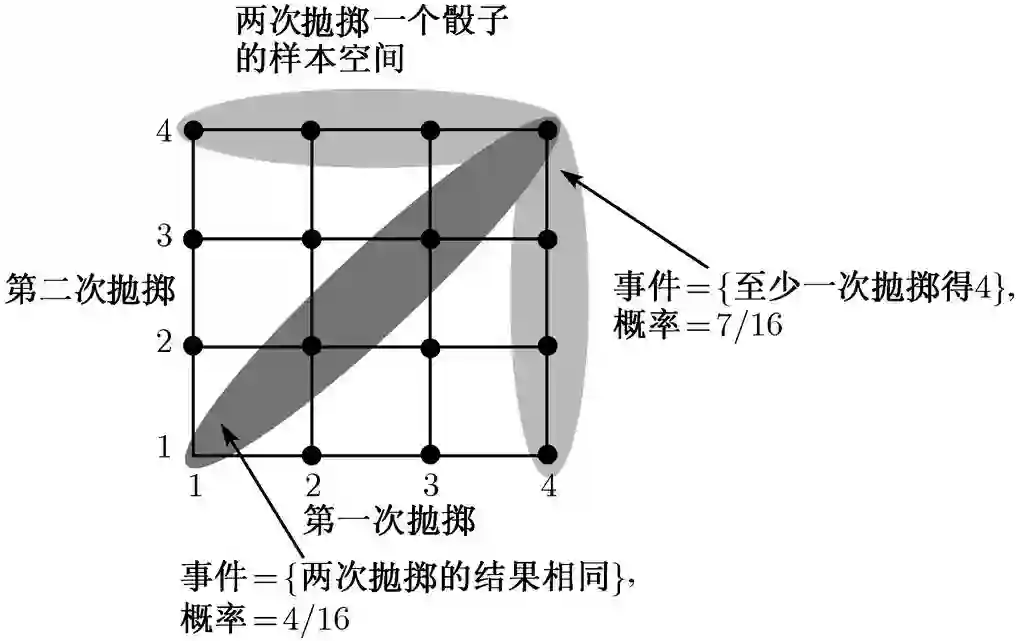
图 1.3　序贯树形图示例.设所考虑的试验连续两次抛掷有4个面的骰子2,其样本空间有两种等价的刻画方法.在这个试验中,可能的结果是全体有序对(i,j ),其中 i 表示第一次抛掷骰子得到的数字,j 表示第二次抛掷骰子得到的数字.试验结果可用左图中的2维格子点表示,也可以用右图中的序贯树形图表示,后者的优点是可以表示试验的序贯特征.在序贯树形图中,每个可能的试验结果可以用一个末端的树叶表示,或等价地用与树叶相联系的由根部到树叶的一个路径表示3.左图中阴影部分代表事件{(1,4),(2,4),(3,4),(4,4)},它表示第2次抛掷得到4.同一个事件可以在右图中用空心圆点标示的叶子集合表示.注意序贯树形图中的每一个结点可以代表一个事件,这个事件就是由这个结点出发的所有的叶子构成的事件.例如,在序贯树形图中用1标示的结点代表事件{(1,1),(1,2),(1,3),(1,4)},即第一次抛掷得1的事件

2当抛掷的骰子有6个试验结果的时候,就是指抛掷常见的正六面体.此处可理解为抛掷正四面体,当落在桌面时,只有一面与桌面接触.本书中的骰子都可以如此解释.——译者注

3用路径表示更能显示试验的序贯特征.——译者注

1.2.4　概率律

假定我们已经确定了样本空间 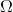 以及与之联系的试验,为了建立一个概率模型,下一步就是要引进概率律的概念.直观上,它确定了任何结果或者任何结果的集合(称为事件)的似然程度.更精确一点说,它给每一个事件A,确定一个数P(A),称为事件A的概率.它满足下面的几条公理.

概率公理

(1) (非负性) 对一切事件A,满足 .

(2) (可加性) 设A和B为两个互不相交的集合(概率论中称为互不相容的事件),则它们的并满足

更一般地,若  是互不相容的事件序列,则它们的并满足

(3) (归一化) 整个样本空间 (称为必然事件)的概率为1,即 .

为了将概率律形象化,可以把样本空间中的试验结果看成质点,每一个质点有一个质量.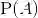 就是这个质点集合的总质量,而全空间的总质量为1.这样,概率律中的可加性公理就变得很直观了：不相交的事件序列的总质量等于各个事件的质量之和.

概率的更具体的解释是频率.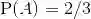 表示：在大量重复的试验中事件A出现的频率约为2/3.这样的解释虽然不总是合适的,但有时却很直观易懂.第5章将会重新讨论这种解释.

概率律有许多重要的性质并没有包含到上述公理系统中,原因很简单,它们可以从公理系统中推导出来.例如,由可加性和归一化公理可得到

由这个性质可知空事件(称为不可能事件)的概率为0,即

现在推导另一个性质,令 、 和  为互不相容的事件,重复利用可加公理,可得到

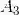
类似的推导可以得到：有限多个互不相容的事件的并的概率等于它们各自的概率之和.后面将讨论更多的性质.

1.2.5　离散模型

现在以实例说明构造概率律的方法.通常我们根据实际试验中的一些常识性假设构造概率律.

例 1.2　考虑抛掷一枚硬币.一共有两种结果,正面向上{H }和反面向上{T }.样本空间为 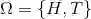,事件为

若硬币是均匀的,即我们相信在抛掷硬币的时候,两面具有相同的机会出现,应该确定两个结果的概率是相等的,即 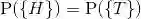.由可加性公理和归一性公理可知

由此可推导得概率律

显然,所建立的概率律满足三条公理.

考虑另一个试验,依次抛掷三枚硬币.试验结果是由正面和反面组成的长度为3的序列.样本空间为

假定上述8种结果的可能性是相同的,即每个结果的概率为1/8.现在利用三条公理建立概率律.例如事件

利用概率律的可加性公理,事件 A 的概率等于组成该事件的试验结果的概率之和：

相似地,任何事件的概率等于1/8乘上该事件中包含的结果的个数.所建立的概率律满足三条公理.

利用概率律的可加性公理以及前面例子中的推理方法,可以得到下面的结论.

离散概率律

设样本空间由有限个可能的结果组成,则事件的概率可由组成这个事件的试验结果的概率所决定.事件  的概率是  之和,即

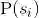
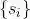
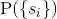
此处用简单的记号  表示事件  的概率,而不用正式的记号 .本书后面都按这个简化的约定书写.

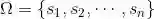
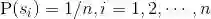
现在设样本空间为 ,并且每个试验结果是等概率的.利用归一化公理可知 ,得到以下定律.

离散均匀概率律(古典概型)

设样本空间由 n 个等可能性的试验结果组成,因此每个试验结果组成的事件(称为基本事件)的概率是相等的.由此得到

现在进一步讨论一些例子.

例 1.3　考虑连续两次抛掷一个有4个面的骰子(见图1.4).现在假定这些骰子是均匀的,这个假定意味着16种可能的试验结果是等可能的,即16种结果的每一种可能的结果(i , j )出现的概率为1/16(i,j =1,2,3,4).这是一个古典概型.在计算一个事件的概率的时候必须数清楚这个事件所包含的试验结果数(基本事件数),将这个结果数除以16(基本事件总数)便得到这个事件的概率.下面几个事件概率就是用这种方法计算得到的.

图 1.4　在连续两次抛掷有4个面的骰子的过程中的若干事件和它们的概率,计算依据离散均匀概率律

1.2.6　连续模型

若试验的样本空间是一个连续集合,其相应的概率律与离散情况有很大的差别.在离散情况下,用基本事件的概率就可以确定概率律,但连续情况却不同.下面是一个例子.这个例子将离散模型中的均匀概率律推广到连续的情况.

例 1.4　在赌场中有一种称为幸运轮的赌具.在轮子上均匀连续地刻度,刻度范围为0到1.当转动的轮子停止时,固定的指针会停留在刻度上.这样,产生的试验结果是[0,1]中的一个数,指针所指向的位置的刻度.因此样本空间是 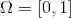.假定轮子是均匀的,因此可以认为轮子上的每一个点在试验中都是等可能的.但一个单点在试验中出现的可能性有多大呢?它不可能是正数,否则的话,若单点出现的概率为正,利用可加性公理,可导致某些事件的概率大于1的荒谬结论.因此单个点所组成的事件的概率必定为0.

在本例中,可定义子区间[a,b]的概率为b-a.更复杂的集合的概率可以定义为这个集合的长度.4这样定义的概率满足概率律的三条公理,因此本例中定义的概率是符合要求的概率律.

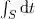
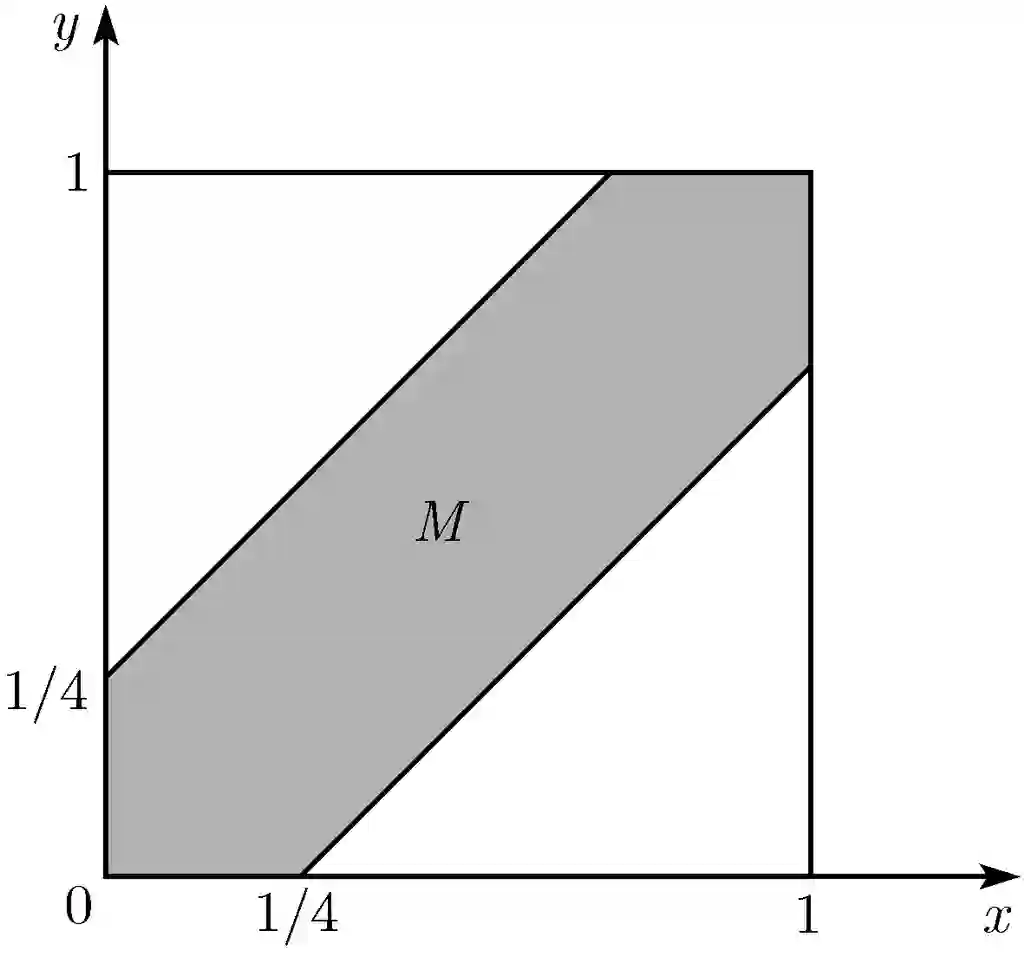
4[0,1]的一个子集 S 的长度定义为 ,对于比较简单的子集,可利用通常的微积分计算这个积分.对于某些不寻常的集合,这个积分可能没有合适的定义,这些事情属于更高深的数学处理的问题.顺便指出,用长度刻画概率律的合法性取决于单位区间是一个不可数无限集.不然的话,由于每个单点的概率为零,可导致[0,1]的概率为0的结论,这与概率的归一化公理相矛盾.

例 1.5　罗密欧和朱丽叶约定在某时刻见面,而每个人到达约会地点的时间都会有延迟,延迟时间在0~1小时.第一个到达约会地点的人会在那儿等待15分钟,等了15分钟后若对方还没有到达约会地点,先到者会离开约会地点.问他们能够相会的概率有多大?

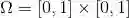
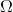
考虑直角坐标系的单位正方形 .正方形中的每个点的两个坐标分别代表他们可能的延迟时间.每个点都可以是他们的延迟时间,而且是等可能的.由于等可能性的特点,我们将  的子集出现的概率定义为这个子集的面积.这个概率律满足三条概率公理.罗密欧和朱丽叶能够相会的事件可用图1.5中阴影部分表示.它的概率等于7/16.

图 1.5　事件 M 代表罗密欧和朱丽叶的相互等待时间不超过15分钟,M 是图中阴影部分(见例 1.5),即

M 的面积等于1减去两个没有阴影的三角形的面积之和,即 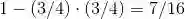.因此,他们能够相会的概率为7/16

1.2.7　概率律的性质

由概率公理可以推导出很多性质,下面列举若干性质.

概率律的若干性质

考虑一个概率律,令 A、B 和 C 为事件.

(a) 若则.

(b) .

(c) .

(d) .

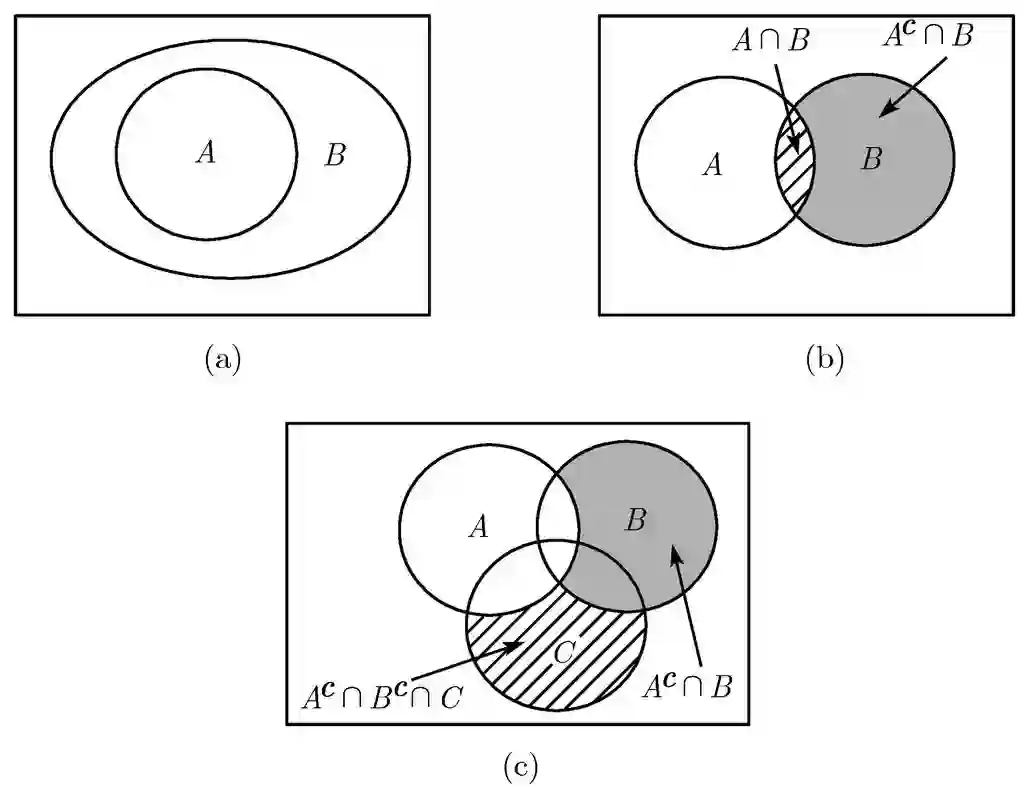
这些性质以及其他类似的性质,都可以形象化地用维恩图证明(见图1.6).注意,性质(c)可以推广成

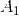
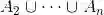
现在证明这个推广的结果.将性质(c)用于事件 和,得到

进一步将性质(c)用于事件 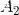 和 ,得到

如此继续下去,最后将诸不等式相加,便得到所需结果.

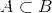
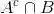
图 1.6　利用维恩图直观地验证概率律的性质(a)、(b)、(c)和(d).设 ,则 B 是两个不相容的事件 A 和  的并(见图(a)).利用可加性公理得

其中不等式利用了概率的非负性公理.性质(a)得证.

由图(b),可将事件 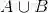 和 B 分解成不相容的事件之并：

利用可加性公理,得到

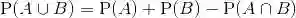
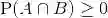
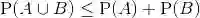
第一式减去第二式并移项得到 ,即性质(b)成立.利用概率的非负性公理得到 ,从而  成立,性质(c)得证.

由图(c),可以看出事件 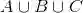 可以分解成三个互不相容的事件的并：

重复利用可加性公理可得到性质(d).

1.2.8　模型和现实

概率理论可以用来分析现实世界的许多不确定现象.这个过程通常分成两个阶段.

(a) 第一阶段,在一个适当的样本空间中给出概率律,从而建立概率模型.在这个阶段,没有关于建立模型的一般规则,只要你建立的概率律符合概率的三条公理就行.有些人会怀疑所建立模型的真实性.有时,人们宁愿使用“错误”的模型,其理由是“错误”的模型比“正确”的模型简单且易于处理.这种处理问题的态度在科学和工程学中很普遍.在实际工作中,选择的模型往往既要准确、简单又要兼顾易操作性.此外,统计学家还依据历史数据和过去相似试验的结果,利用统计方法确定模型.这将在第8章和第9章讨论.

(b) 在第二阶段,我们将在完全严格的概率模型之下进行推导,计算某些事件的概率或推导出一些十分有趣的性质.第一阶段的任务是建立现实世界与数学的联系,而第二阶段则是严格限制在概率公理之下的逻辑推理.在后一阶段,如果涉及的计算很复杂或概率律的陈述不简明,推理和理解就会遇到困难.但是所有的问题将会有一个准确的答案,不会产生歧义.只要有足够高的能力,所有的困难都将化为乌有.

在概率论中充满这样的“悖论”：对同一个问题,不同的计算方法似乎会得到不同的结论.在这种模棱两可的概率律中选定模型会导致结论的不确定.贝特朗悖论是一个著名的例子(见图1.7).

图 1.7　贝特朗悖论.该例子由贝特朗于1889年提供,它说明这样一个原理：解决一个实际问题的时候,必须建立无歧义的概率模型.设在一个圆内有一个正三角形,内接于圆周.现在随机地选定一个弦,问其长度大于内接正三角形的边的概率等于多少?其解答依赖于“随机地选定”的确切定义.图中(a)和(b)的两种方法导致相互矛盾的结论.

在图(a)中,取一半径 AB,在 AB 上随机地取一个点 C .所谓随机地取点是指 AB 上所有的点具有相同的机会被取到.通过点 C ,作一条弦垂直于 AB .由初等几何的知识可知,当 C 点的位置恰巧在 AB 的中点时,弦的长度刚好等于三角形的边长,而远离圆心时,弦的长度减小.这样弦的长度大于内接正三角形的边长的概率等于1/2.

在图(b)中,圆周上取一点 V 作为顶点.通过 V 先画一条切线,然后随机地画一条通过 V 的直线.记直线与切线的夹角为 .由于这条直线是随机地画的,可以认为夹角 是在 上均匀地分布的.现在考虑这条直线割圆得到的弦的长度.由初等几何的知识可知,当  处于  的范围内,弦的长度大于三角形的边长.由于  取值于 ,故这根弦大于内接正三角形边长的概率是1/3