概率质量函数与累积分布函数-连续
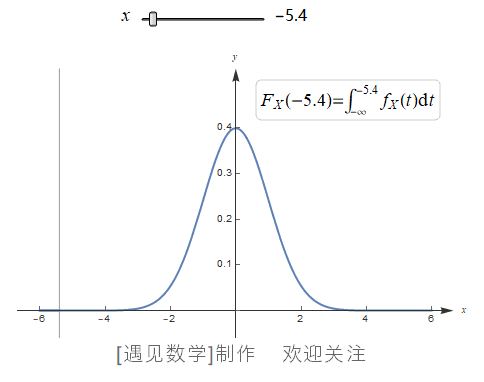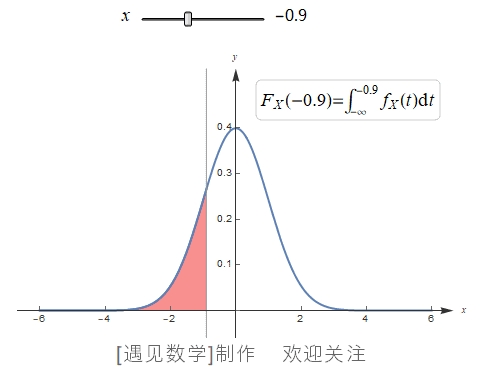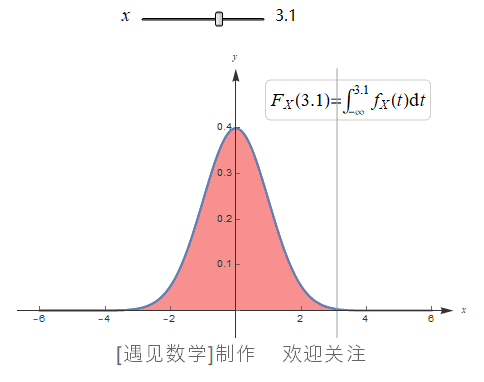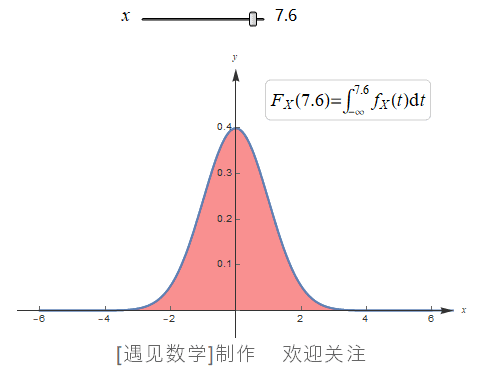
当累积分布函数为连续函数时候, 概率质量函数 PMF 不再适用, 因此就需要用积分(概率密度函数PDF)来计算概率. 在概率中, PDF 是 CDF 的微分, CDF 是 PDF 的积分, 观察下面以标准正态分布为例的 PDF 与 CDF 关系动画:
![]()
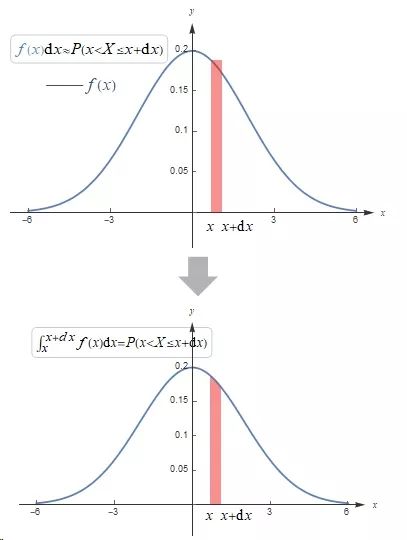
与PMF不同, 概率密度函数(Probability Density Function, PDF) f(x)与 dx的乘积约等于概率, 即 f(x) dx ≈ P(x<X<=x+dx), 观察下图中的浅红色阴影部分, 如果将该范围内的PDF积分, 就会得到该范围的概率.
![]()
均匀分布(Uniform Distribution)
连续型随机变量 X 具有如下的概率密度函数,则称 X 服从[a,b]上的均匀分布(uniform distribution),记作 X ~ U(a, b)
![]() 均匀分布的 PDF 和 CDF 如下:
均匀分布的 PDF 和 CDF 如下:
![]()
正态分布(Normal Distribution)
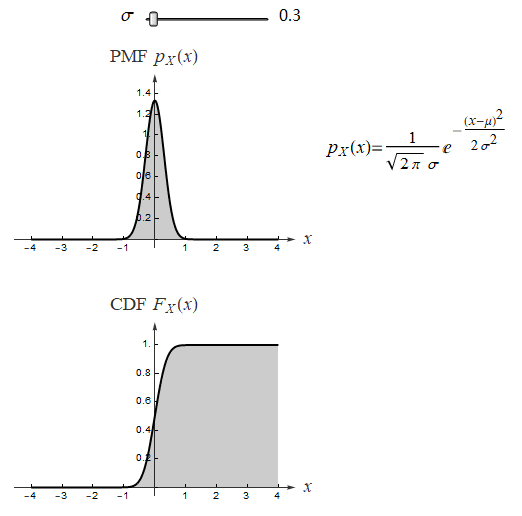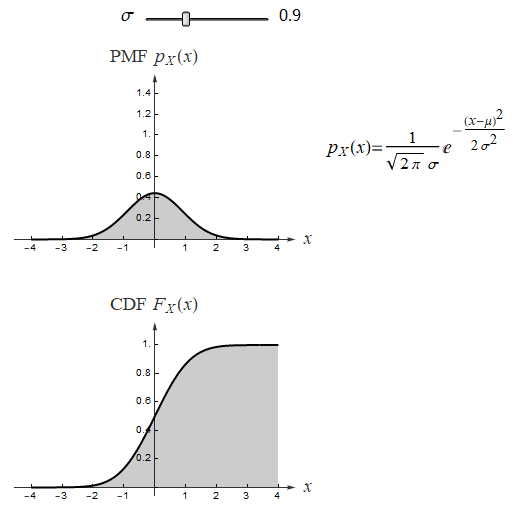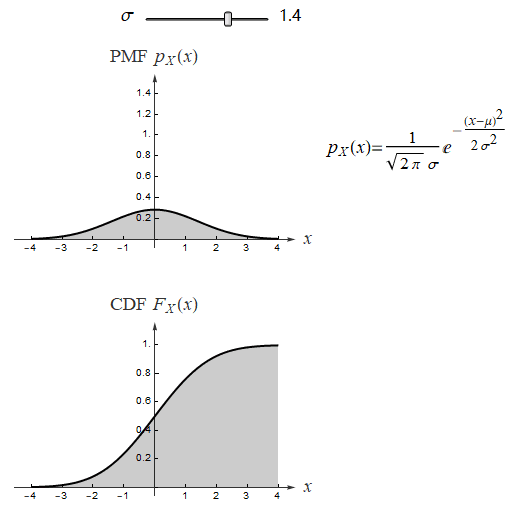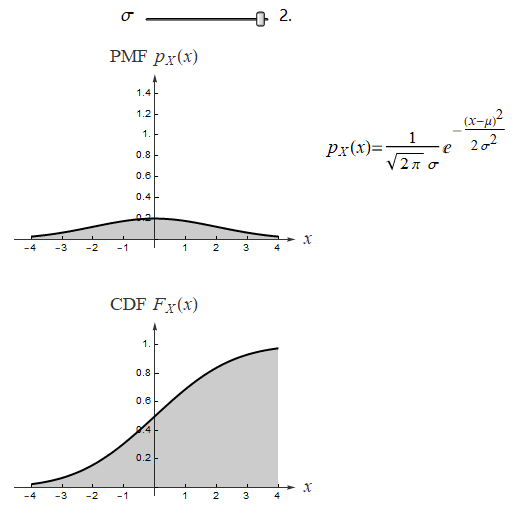
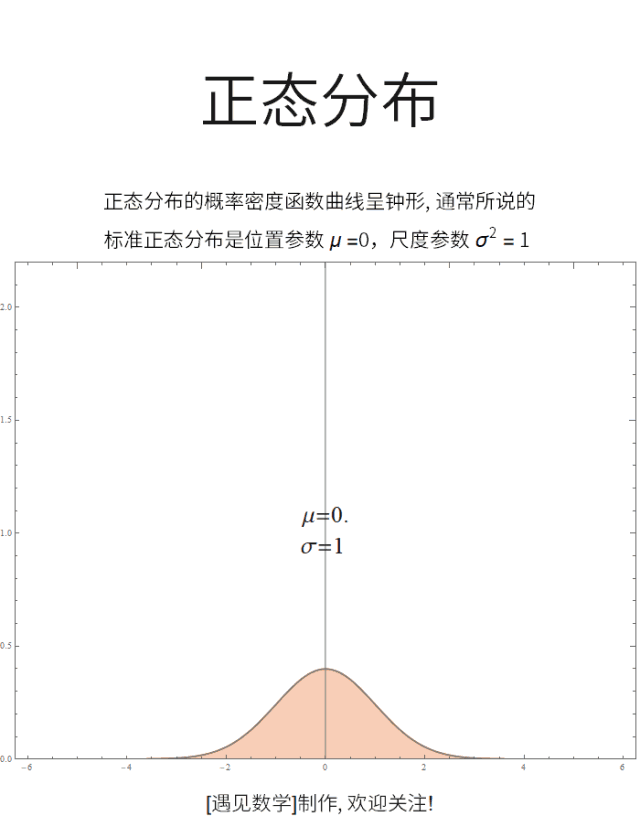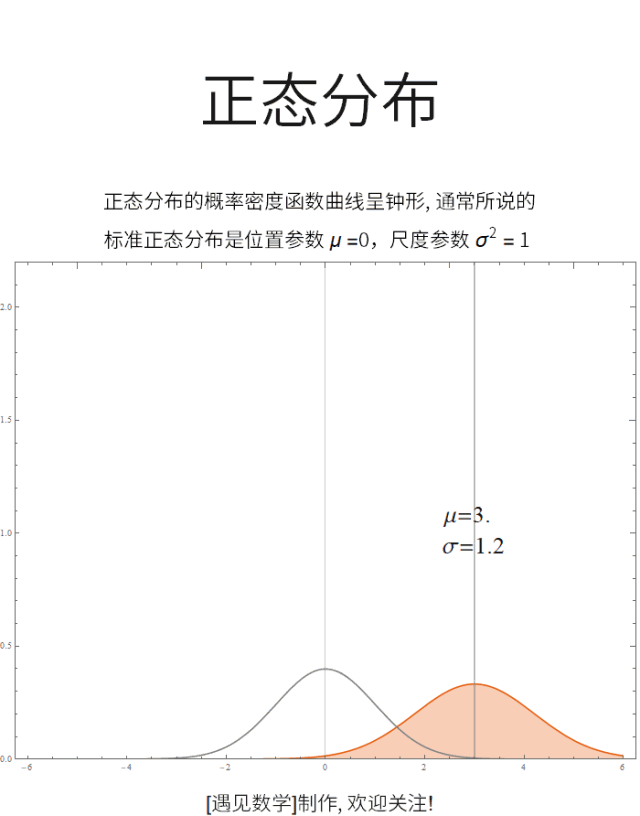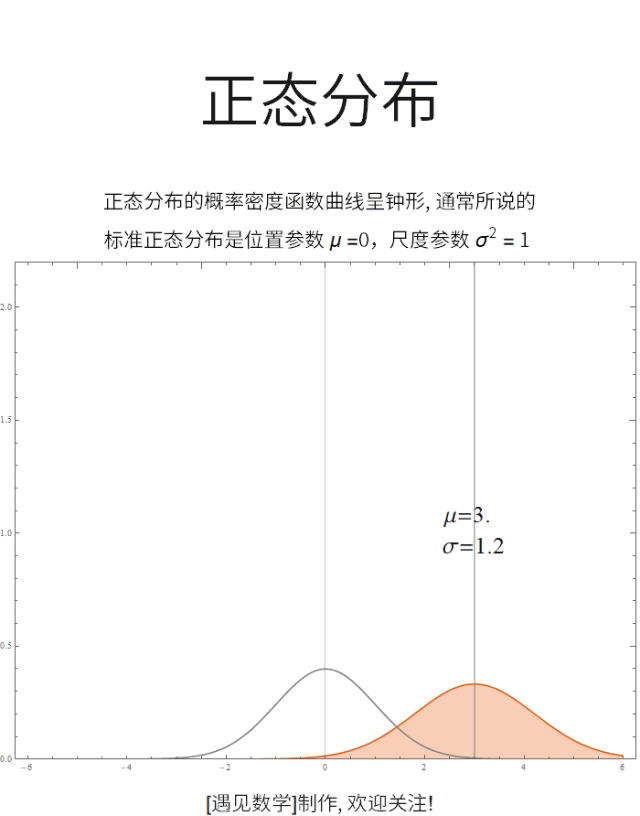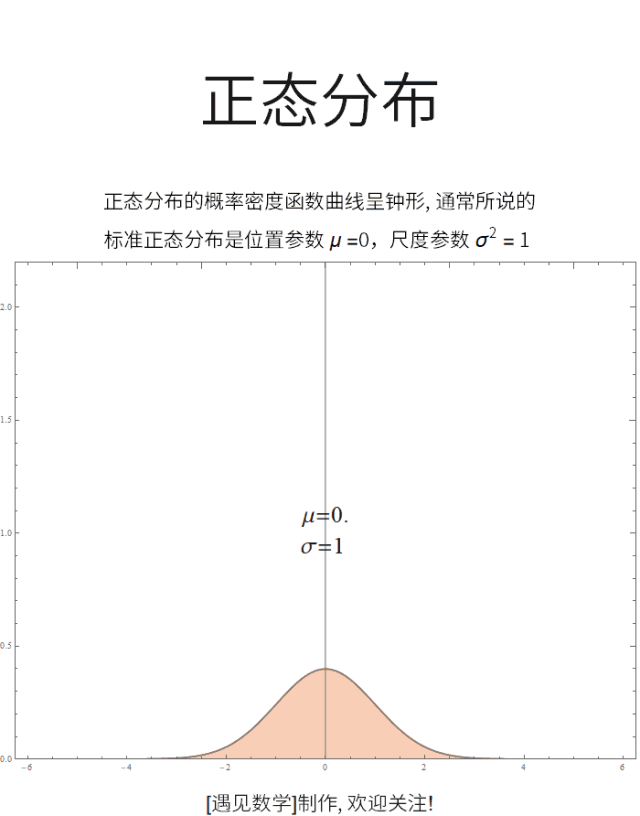
正态分布是在统计以及许多统计测试中最广泛应用的一类分布, 很多自然现象都服从正态分布. 若随机变量 X 服从一个位置参数为 μ 、尺度参数为 σ 的正态分布,记为:X ~ N(μ, σ²)
![]() 正态分布的数学期望值或期望值 μ 等于位置参数,决定了分布的位置;其方差 σ²的开平方或标准差 σ 等于尺度参数,决定了分布的幅度。观察下面动图:
正态分布的数学期望值或期望值 μ 等于位置参数,决定了分布的位置;其方差 σ²的开平方或标准差 σ 等于尺度参数,决定了分布的幅度。观察下面动图: ![]()
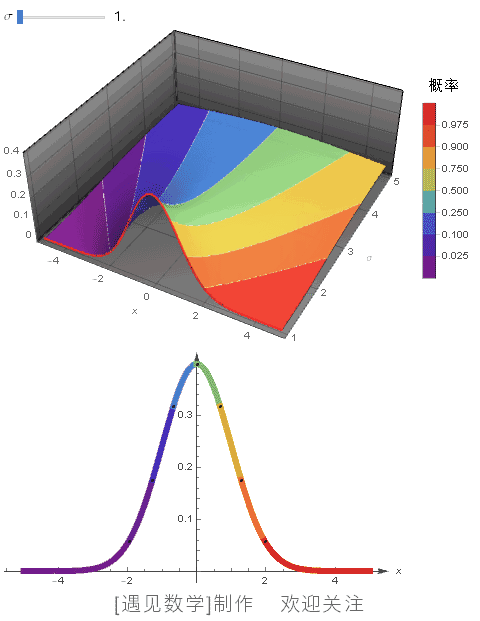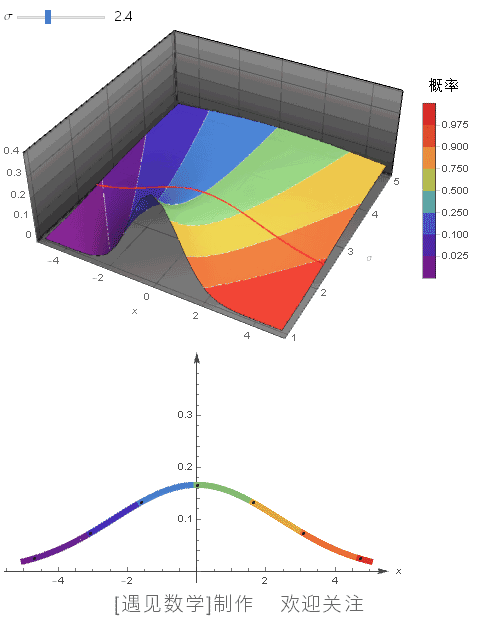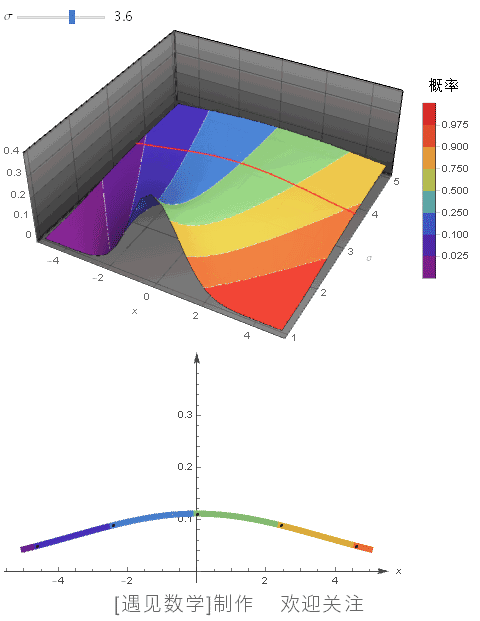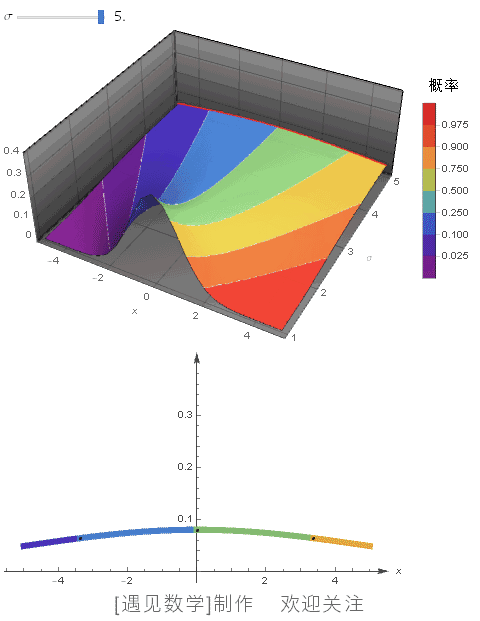
μ=0 时, 绘制不同 σ 值的概率密度函数,同时显示 CDF 等高线:
![]()
指数分布(Exponential Distribution)
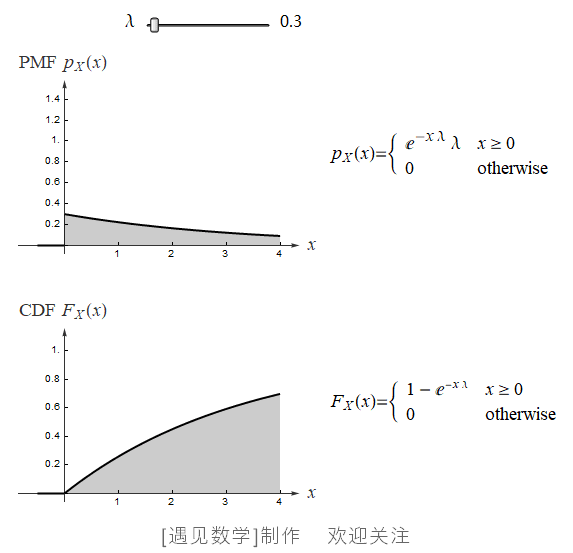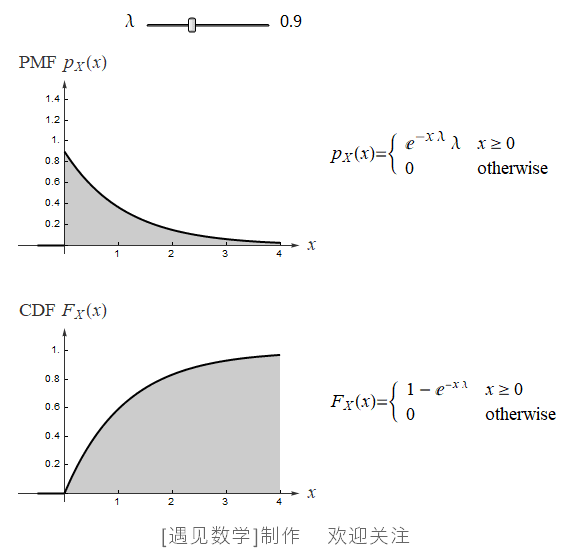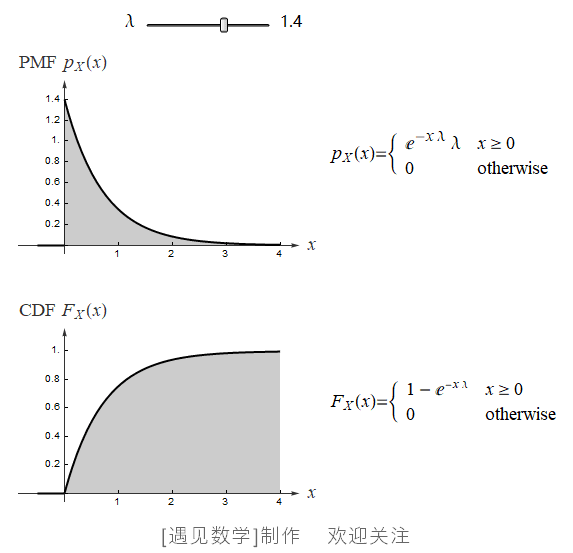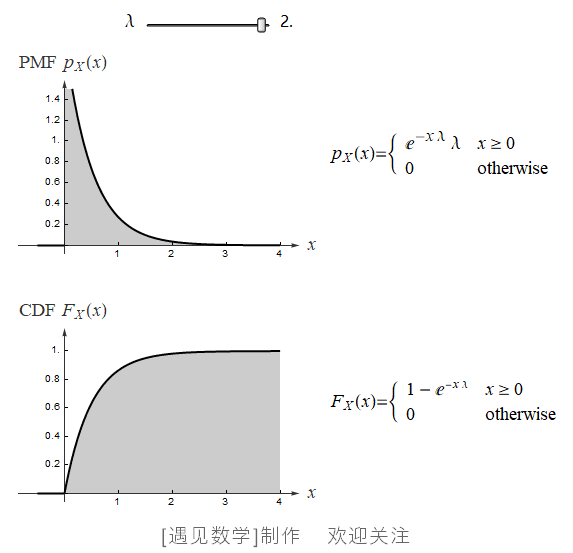
指数分布可以用来表示独立随机事件发生的时间间隔, 比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔等等. 若随机变量 X 服从参数为 λ 的指数分布,则记为 X~Exp(λ) . 其中 λ > 0 是分布的一个参数, 即每单位时间发生该事件的次数. 指数分布的区间是 [0,∞). 观察下面指数分布的 PDF 与 CDF 动图:![]() 绘制不同 λ 值(0.1~5)的概率密度函数,同时显示 CDF 等高线, 观察下面动画:
绘制不同 λ 值(0.1~5)的概率密度函数,同时显示 CDF 等高线, 观察下面动画:
![]()
伽玛分布(Gamma Distribution)
伽玛分布有两个: 参数 α 称为形状参数,β 称为尺度参数, α>0, β>0.
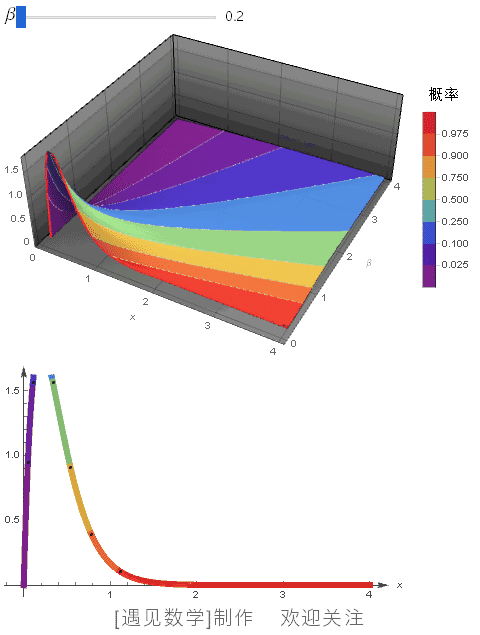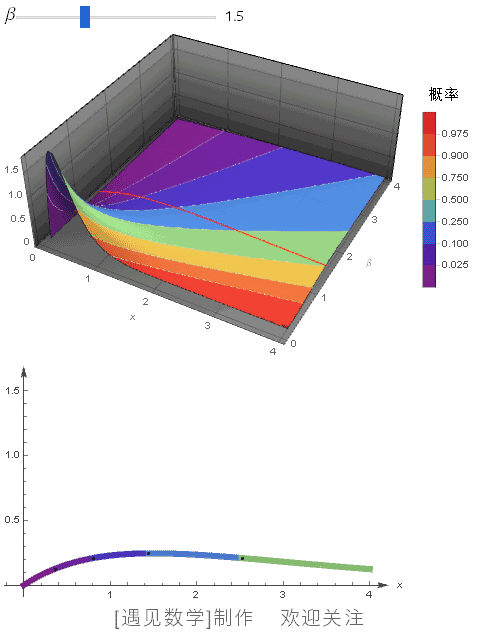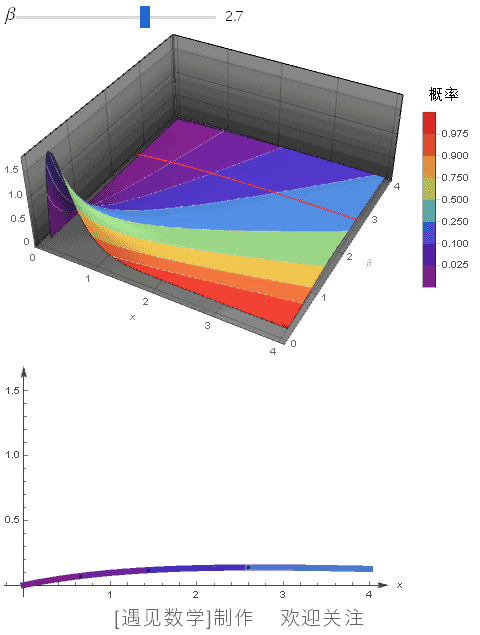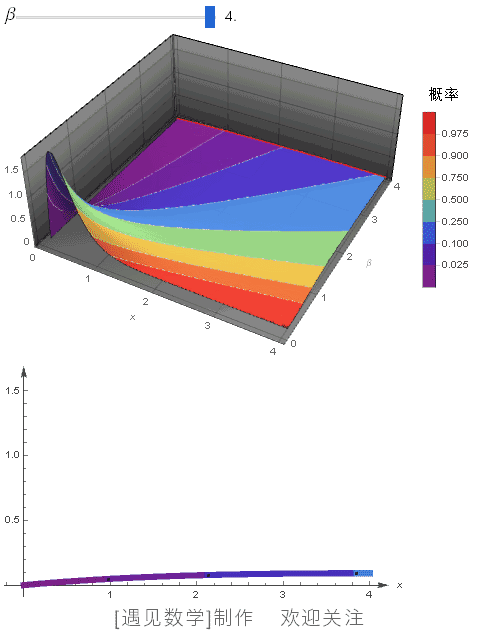
![]() 在 CDF 等高线下,当 α=2 时, 不同 β 值的概率密度函数, 观察下面动画:
在 CDF 等高线下,当 α=2 时, 不同 β 值的概率密度函数, 观察下面动画:
![]()
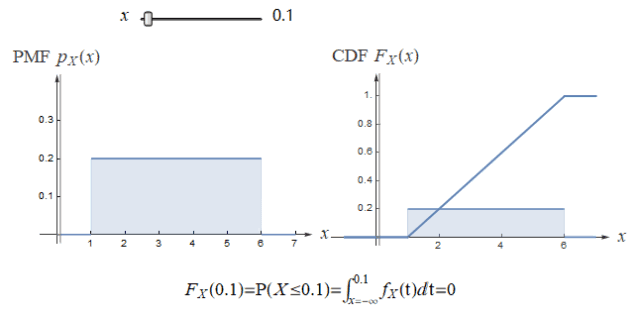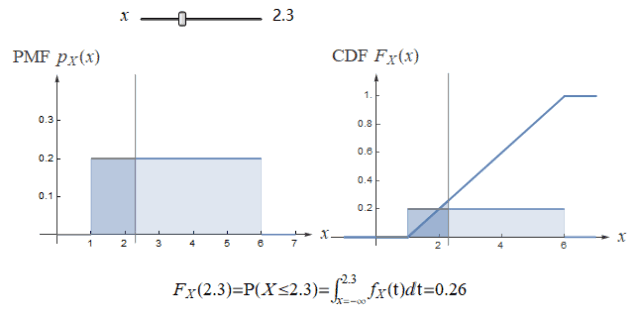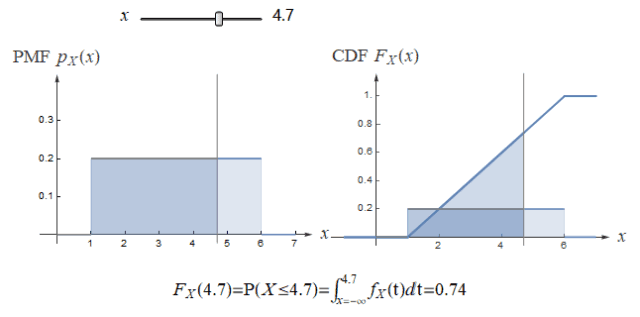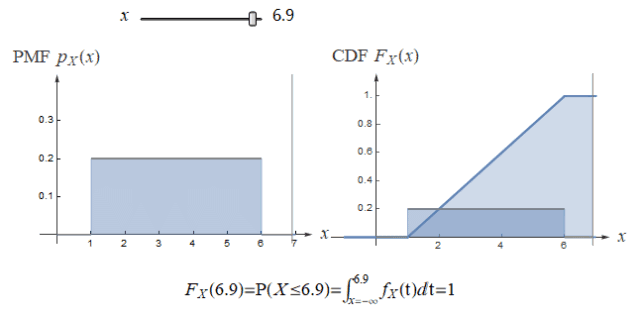 均匀分布的 PDF 和 CDF 如下:
均匀分布的 PDF 和 CDF 如下: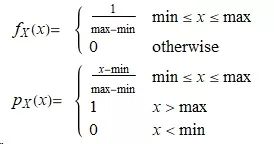
 绘制不同 λ 值(0.1~5)的概率密度函数,同时显示 CDF 等高线, 观察下面动画:
绘制不同 λ 值(0.1~5)的概率密度函数,同时显示 CDF 等高线, 观察下面动画: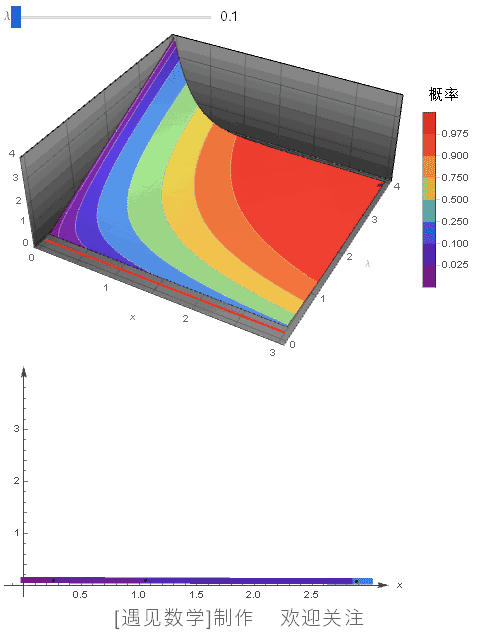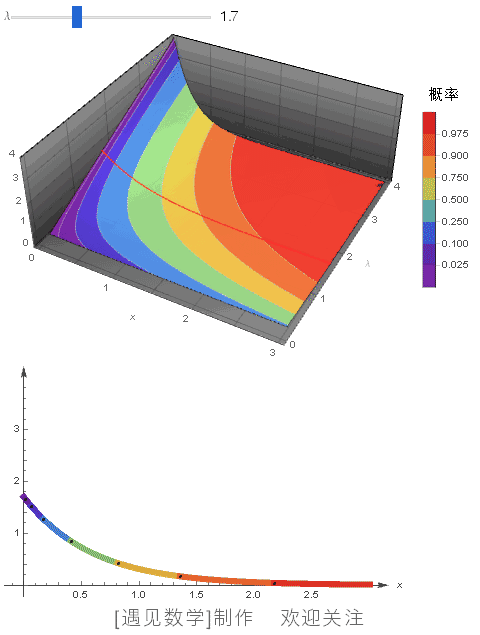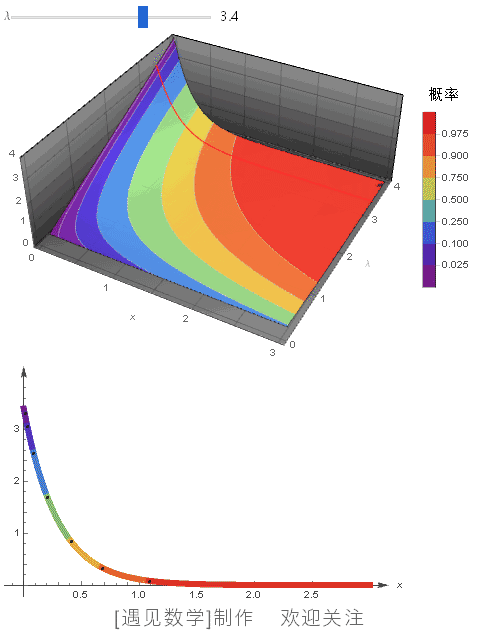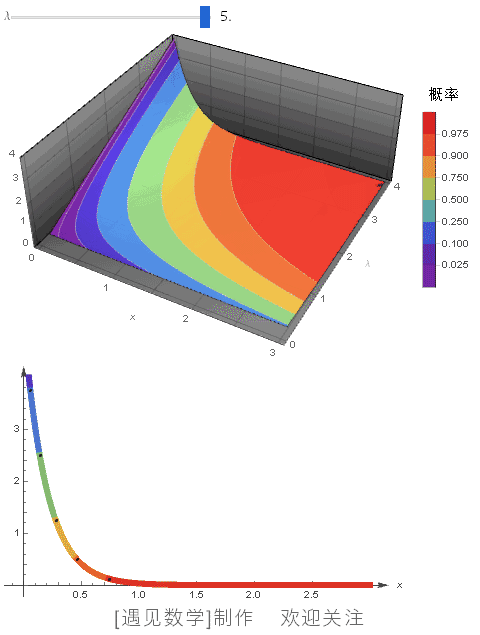
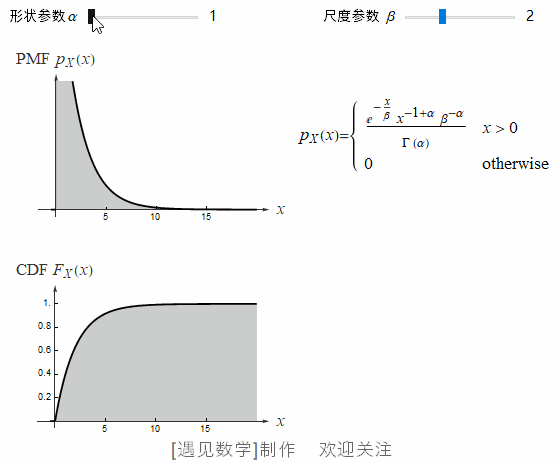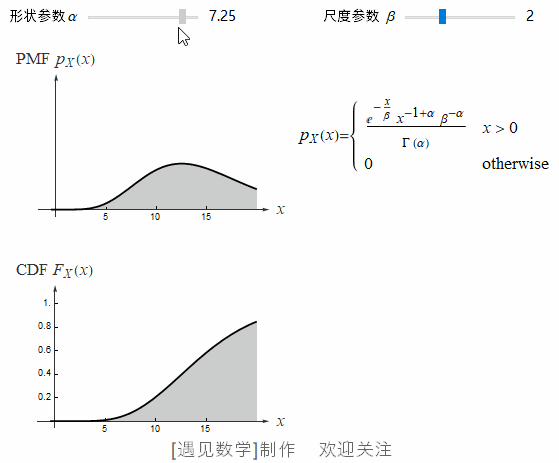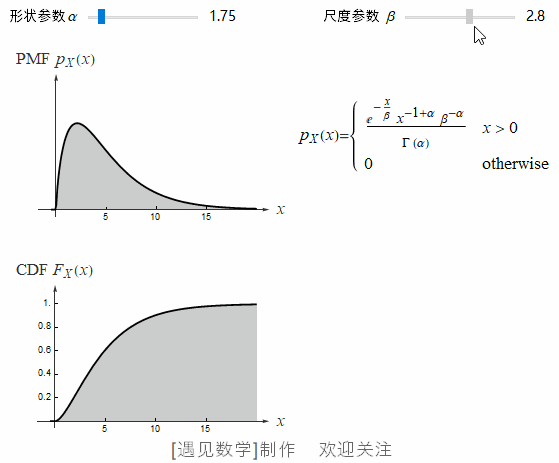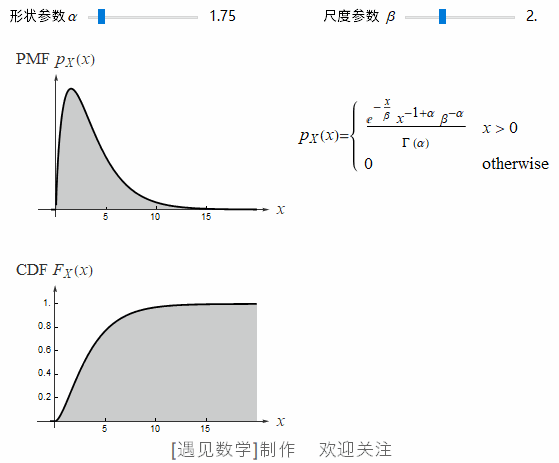 在 CDF 等高线下,当 α=2 时, 不同 β 值的概率密度函数, 观察下面动画:
在 CDF 等高线下,当 α=2 时, 不同 β 值的概率密度函数, 观察下面动画: