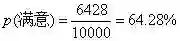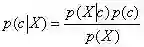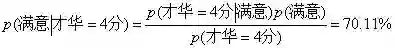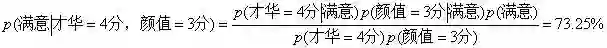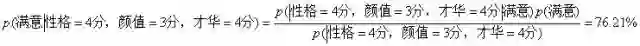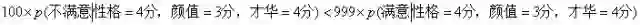遇上对的 Ta 到底概率有多高，贝叶斯告诉你答案

2018 年 12 月 11 日 中科院物理所

贝叶斯（约1702-1761）Thomas Bayes，英国牧师、数学家，创建了贝叶斯统计理论，对于统计决策函数、统计推断、统计估计等方面做出了贡献，同时也是可劲折腾大学生、AIer的大佬之一。

贝叶斯决策论是一种解决分类问题的基本方法，其与众不同之处在于：充分利用概率的不同分类决策与相应的决策代价之间的折中。在先验概率的基础上，考虑最大似然函数，我们可以利用最大后验概率进行分类决策。若再考虑决策的代价或者损失，就成了贝叶斯决策论······额，经过小编的发奋钻研，发现贝叶斯决策论可以很好得解释一下女孩子的恋爱行为！

小编以某种方式建立了一个数据集，对10000个男生从性格、颜值、才华三个方面进行打分（1~5分），然后让女孩评价对其是否满意。

接下来，我们一起来看一些有趣的事情：

第一天

小A是一名单身女孩，突然有一天，小A的闺蜜小B神秘兮兮要给她介绍男朋友，但是具体内容一字未提。晚上，小A妹子辗转反侧，不断琢磨着：她会介绍谁呀？条件怎么样嘞？不知道能不能谈得来......这时，根据样本中的“经验”（6428个满意，3572个不满意），小A大概估计了下对未谋面男孩的满意概率：

分析：即使没有任何信息，仅靠平白无故的直觉，小A遇到如意郎君的概率毕竟有一多半呢！所以，世上还是好人多呀。

第二天

小B中午吃饭的时候，神秘得透露给小A，这个男孩的才华有4分呢。哎呦？不错哦，小A一边有点开心，一边对自己的满意概率进行了调整，根据大名鼎鼎的贝叶斯公式：

在仅知道男孩的才华为4分的时候，满意概率为：

分析：当得到男孩的更多信息时，小A便可以运用贝叶斯公式做出更好的判断，明显可以看出后验概率70.11%已经比先验概率64.28%提升了不少。同时，如果男孩是顶级学神，才华=5分，那么这个概率会提升到74.41%！！！

第三天

小A不知道从哪里搞到了男孩的照片，认真打量一下，挺好的，不至于是超级大帅哥但是看着比较踏实稳重，颜值至少3分吧。就当颜值3分的吧，这个时候，小A再次偷偷调整自己的满意概率。

在知道男孩的才华为4分，颜值为3分的时候，满意概率为：

分析：显而易见，更多的信息有助于做出更准确判定。颜值=3分帮小A获得了一个信息，男孩子有才华，颜值不差，所以满意概率会有些许上升。另外，聪明的小A在计算概率时，为了简化计算，假设才华与颜值没有任何关系、彼此独立，这便是所谓的“朴素贝叶斯（样本的特征之间彼此无关）”。

第四天

今天，小B决定让这两位互相见见面，认识一下。小A在小B的陪伴下，把自己打扮得美美哒，跟这位男孩一起吃晚饭。谈吐之间，男孩子热情大方开朗，小A对此印象甚是不错。于是乎，小A对最终其打分为性格4分，颜值3分，才华4分。小A当场迅速得计算了下：我跟这位男孩谈恋爱，将来能有多大的概率最终感到满意呢？

分析：换一个角度来思考小A的历程，小A在未了解男孩的任何信息的时候，她有35.72%的概率对男孩子不满意，可能是担心男孩的样子她不喜欢，担心他性格暴躁等等；当知道男孩才华为4分时，她的疑虑有所打消，故不满意的概率下降为29.89%；然后每一次得到更多有益的信息，小A的疑虑都会有一定程度的下降。但注意，即使如此，这个性格4分，颜值3分，才华4分的男孩仍然有23.79%的概率使小A不满意，这或许可以用“有缘无分”来解释吧，贝叶斯大爷也无能为力。

第五天

小A开始最后的纠结，她要做出决定：是不是要开始进行这段恋爱关系？

小B：你不是对人家挺满意的嘛？那就去试一试呗。

小A：你说的不错呀，但是我只有76.21%的把握对其满意呀。

小C（小A的舍友）：我比较谨慎小心，如果他是一个不满意的男孩，而我把他误认为满意的男孩，那得多痛心疾首啊。如果是我，我更可能拒绝他。四分之一的出错概率呢，还是不低呀。

小A（沉思片刻）：我们可以利用“贝叶斯决策理论”来解决。嗯······对于我而言，把一个不满意的男孩误认为是满意的男孩会对我影响不算大，就当有100点影响吧；但是把一个本应感到满意的男孩认定成不满意的男孩，我觉得会受到999点影响，然后

，我应该认定这是一个满意的男孩。

小B：......

小C：......

分析：小A在最终做决策时，不仅利用了后验概率，还充分考虑了做出错误决策的代价损失。经过计算，这个男孩对小A而言，最终决策是判定为满意男孩；而同样的问题，小C的计算结果则会将其判定为不满意男孩，因为小C十分担心不满意男孩误判成为满意男孩的问题。

从概率到贝叶斯公式再到贝叶斯决策，我们的决策越来越科学合理。这是因为，我们逐渐加入了更多的信息（比如男孩的才华、颜值等），加入了小A的风险偏好（两种误判对小A的影响）。这是一种机器学习非常基本、有效的方法，当然，其实小A还可以使用方法，比如LDA或者决策树等等也同样有不错的效果。不过，您可千万别忘了，既然是机器学习，它一定要从“数据集”中学习，比如本例中的那10000条数据。没有数据集供我们学习的话，整个流程将无法进行一丝一毫，甚至规模较小的数据集、不符合真实世界的数据集都无法得到令人信服的结果。

话付前言，小A最终也找到了自己的幸福，因为：