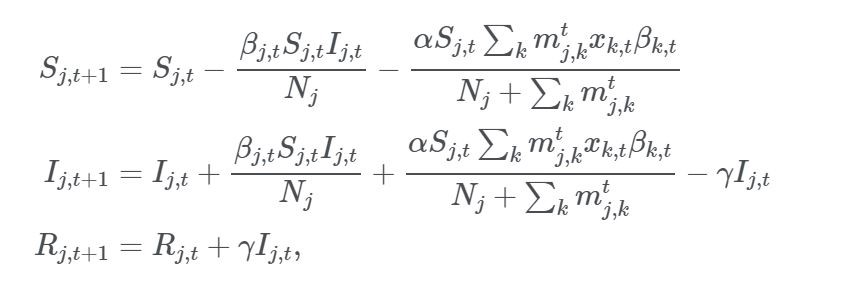疫情之下，这是你也能上手的Python新冠病毒传播建模教程（附代码）

2020 年 2 月 16 日 机器之心

选自 towardsdatascience

作者：Gevorg Yeghikyan

机器之心编译

机器之心编辑部

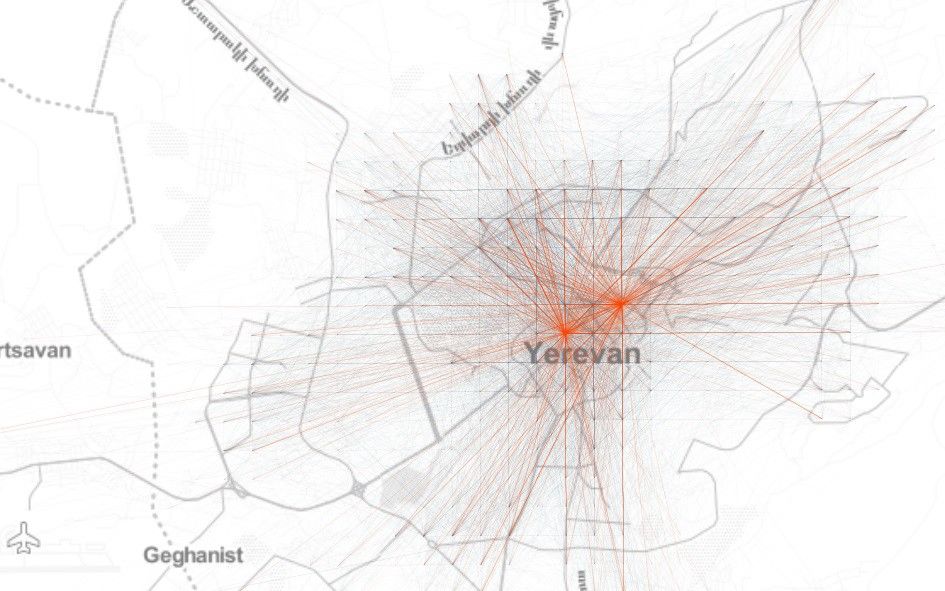
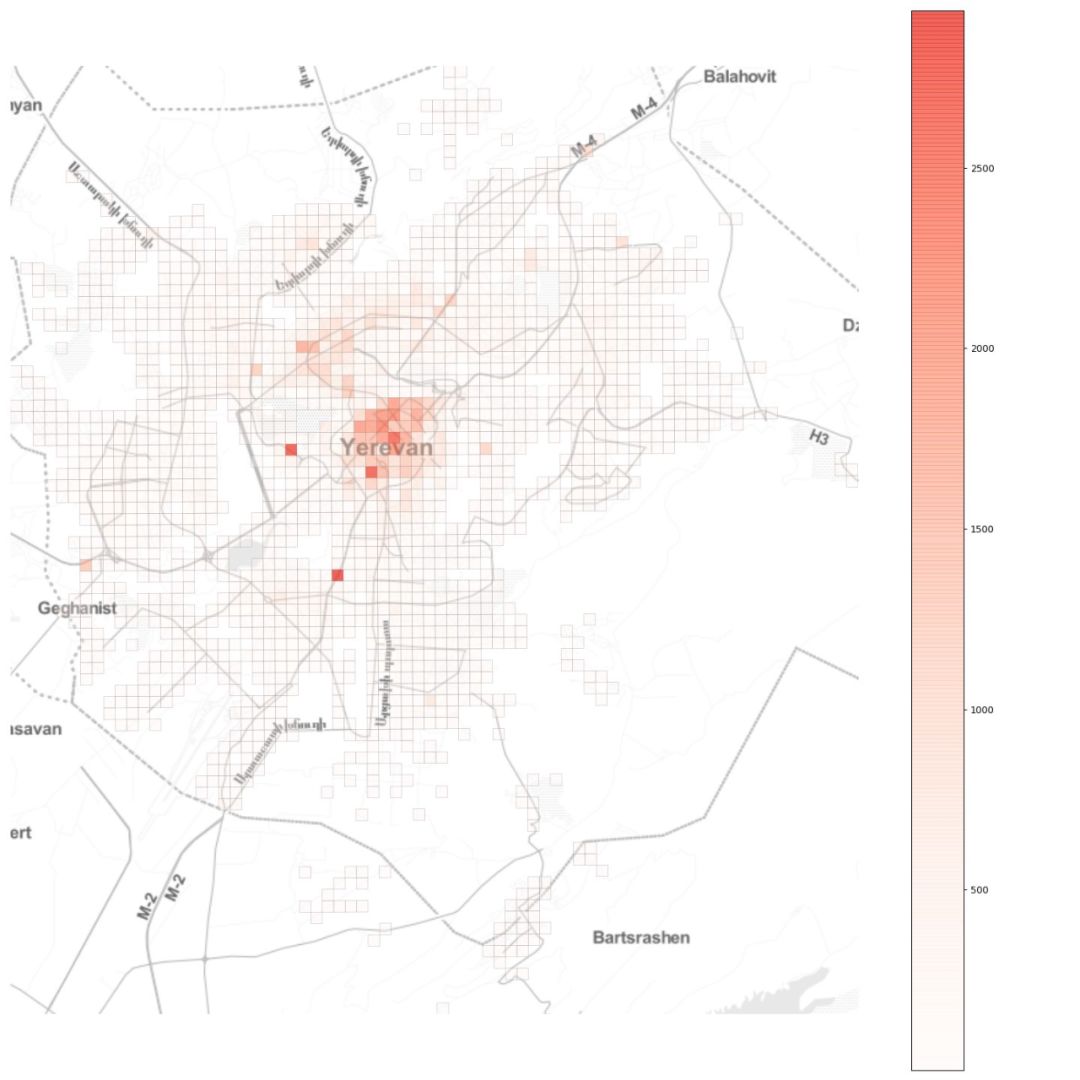
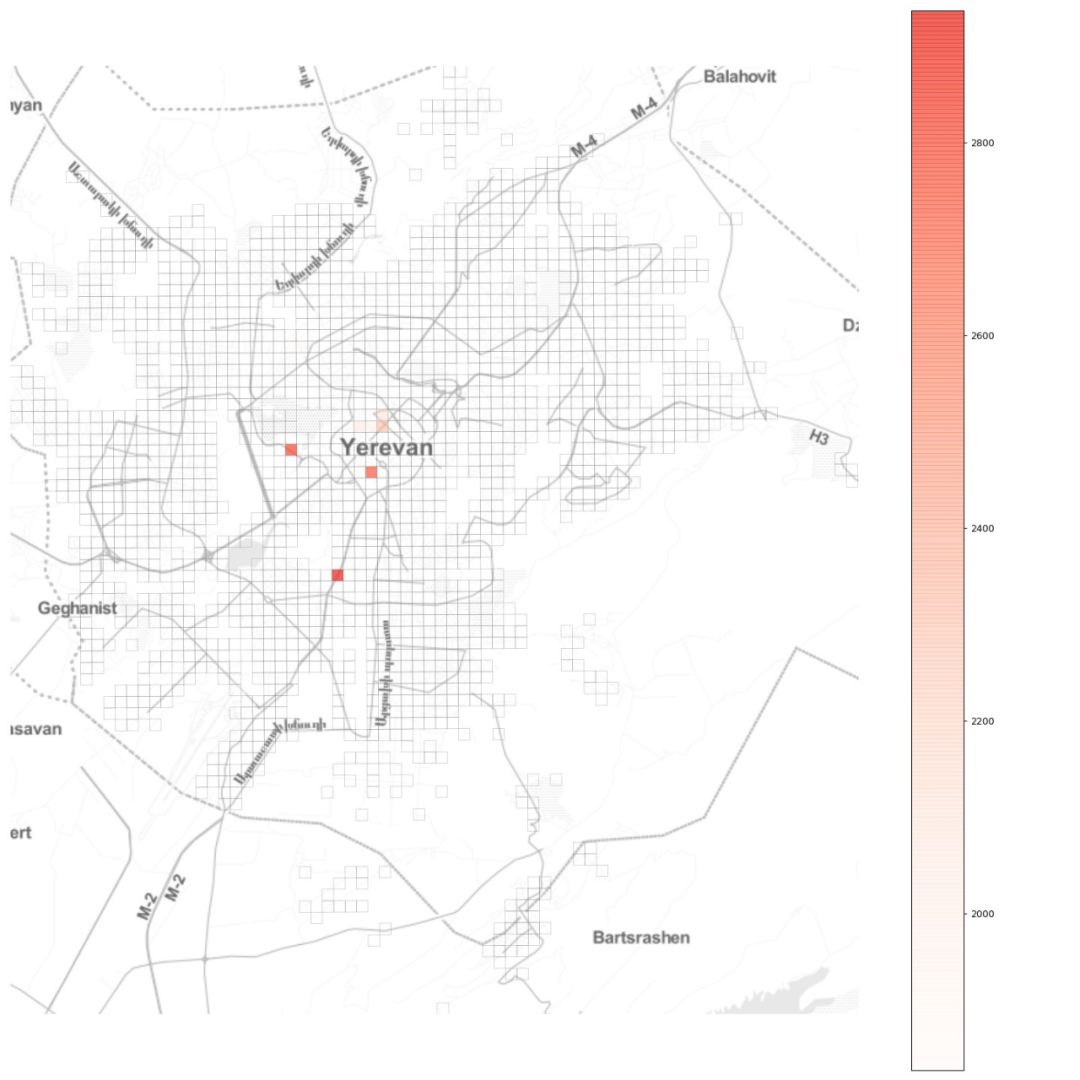
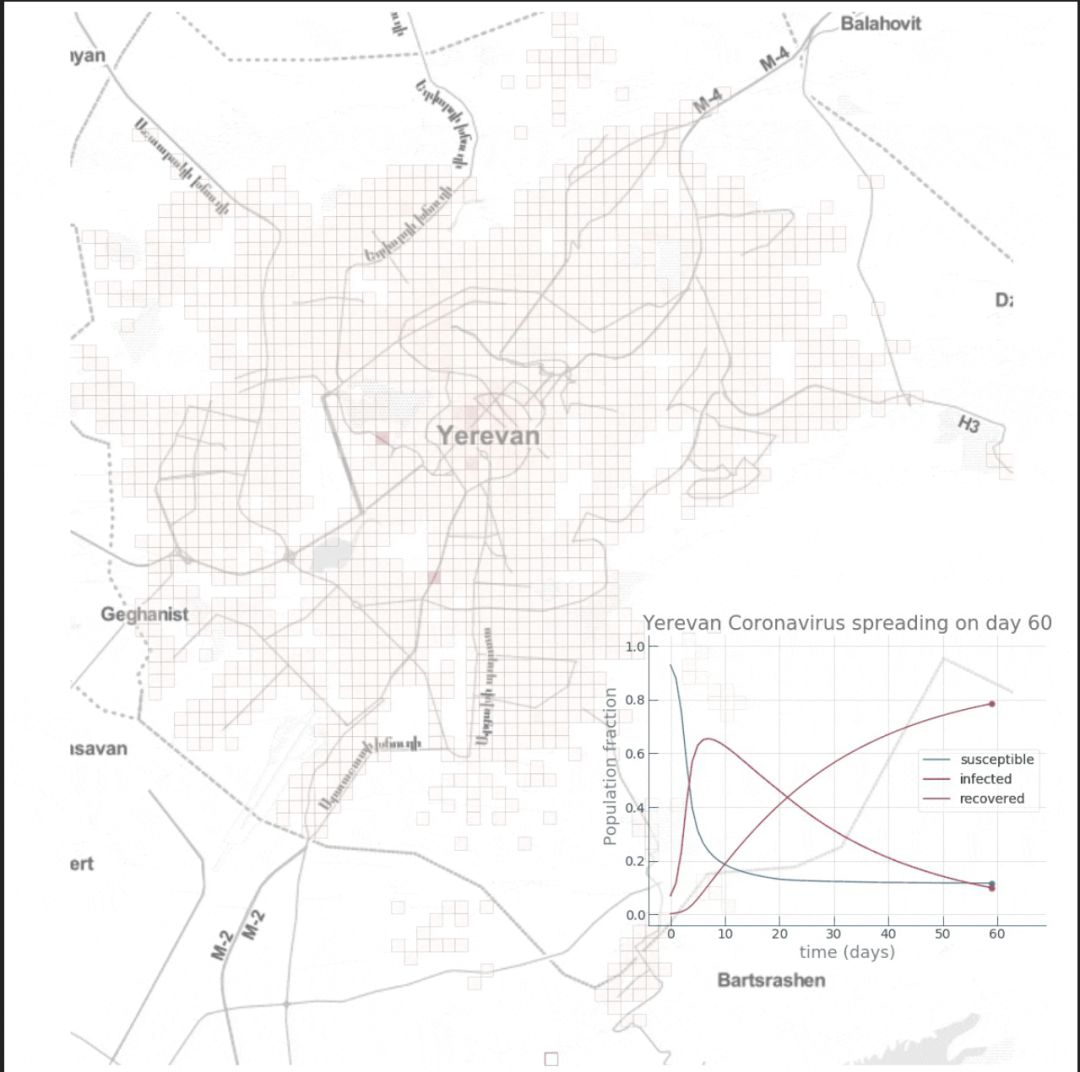
自去年12月以来，新型冠状病毒所引发的疫情已经给城市活动带来了很大影响。怎样确切了解病毒的传播过程，从而帮助城市更好提出措施？使用建模的方法也能起到一些作用。本文是一篇Python教程，教你在家中也可以建模疫情传播。本文以亚美尼亚共和国首都埃里温作为案例，对冠状病毒在该城市中的蔓延情况进行数学建模和模拟，并观察城市流动模式对病毒传播的影响。读者也可根据文末的示例代码，自己上手使用。

目前，尚未发现经医疗研究标准确认的特效药。此外，很多重要的流行病学指标仍属未知，如基本传染数 R0（在流行病学上，基本传染数指在没有外力介入，同时所有人都没有免疫力的情况下，一个感染到某种传染病的人，会把疾病传染给其他多少个人的平均数）。新型冠状病毒还存在很多的不确定性。

如今的全球社会，联通度和流动性空前。由于小世界效应，这类流行病对全球造成重大威胁。有人猜想如果 2020 年发生全球性灾难事件（粗略定义为伤亡人数大于 1 亿），那么最可能的原因是某种流行病，而不是核灾难、气候灾难等。全球城市化的快速发展更加强化了这一点，因为人口密集的城市变成了疾病扩散网络中的传播节点，因而变得极度脆弱。

本文将探讨当一座城市遭受流行病袭击时会发生什么，应立即采取哪些措施，以及这些措施对城市规划、政策制定和管理带来的影响。本文以亚美尼亚共和国首都埃里温作为案例，对冠状病毒在该城市中的蔓延情况进行数学建模和模拟，并观察城市流动模式对病毒传播的影响。

城市流动

高效持续的城市流动对现代城市的运转举足轻重，并直接影响城市的宜居性和和经济输出（GDP）。但是，当流行病爆发时，城市流动却火上浇油，推动了疾病的传播。

我们先来看埃里温市起讫点（origin-destination，OD）交通流以聚集的方式在均匀笛卡尔网格上形成的网络，以便了解城市流动模式的空间结构：

仔细观察网格单元的总体流入情况，你会看到一个单中心空间组织，位于中心的单元格具备高日流入量：

现在，假设流行病在这座城市的随机地点爆发了。它将以怎样的方式扩散？怎么做才能控制住它？

建模流行病

为了解答以上问题，我们先构建一个简单的房室模型（compartmental model）来模拟传染病在城市中的扩散。在传染病爆发时，根据首次感染发生地点及其与城市其它地区的连通性，其传播动态存在显著差异。这是近期对城市人口流行病进行数据驱动研究后得出的最重要结论之一。但是，虽然病毒传播状况不同，但城市需要采取类似的措施来控制传染病，以及执行城市规划和管理。

个人运行流行病模型难度很大，因此本文旨在展示流行病在城市中的一般传播原理，而不是构建精细准确的流行病模型。本文将按照 Nature 文章《Multinational patterns of seasonal asymmetry in human movement influence infectious disease dynamics》中介绍的方法进行操作，并根据具体需求修改了经典 SIR 模型。

该模型将城市人口分成三室。对于时间点 t 处的每个地点 i，这三室分别是：

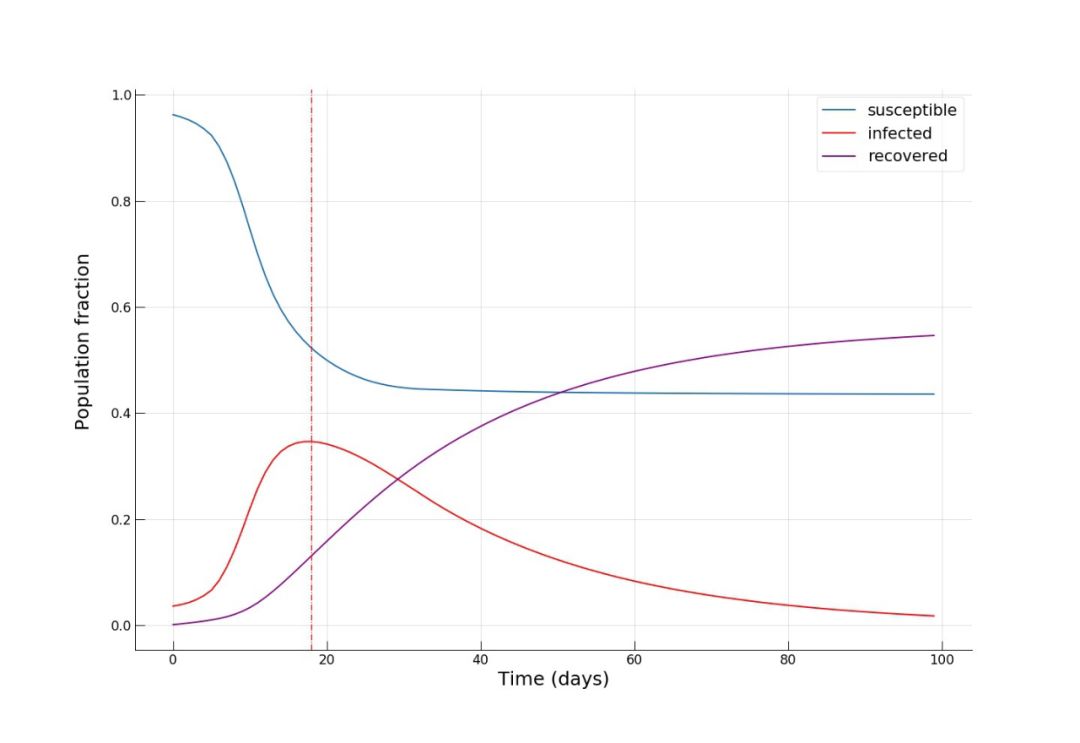
S_i,t：尚未感染或易感人群（易感组）；
I_i,t：感染该疾病且具备传染性的人口（感染组）；
R_i,t：感染疾病后，由于痊愈或死亡从感染组移出的人口。这组人不再感染病毒，也不会将病毒传播给他人。

在此次模拟中，时间是离散变量，因为系统状态是在每天的基础上建模的。假设第 t 天地点 j 处的所有人均未感染该疾病（易感人群），则此处出现病例的概率为：

其中 β_t 是第 t 天的传染率，m_j,k 表示从地点 k 到地点 j 的流动情况，x_k,t 和 y_j,t 分别表示第 t 天地点 k 处的感染者比例和地点 j 处的易感人群比例，x_k,t = I_k,t / N_k, y_j,t = S_j,t / N_j，其中 N_k、N_j 分别表示地点 k 和 j 处的人口规模。

接下来我们来模拟将疾病带入易感人群所在地区的随机过程，I_j,t+1 是伯努利随机变量，概率为 h(t,j)。

一旦病毒传播到随机地点，则它们不仅在这些地点传播，还会随流动人口向其他地点扩散。这就是城市流动模式的重要影响（城市流动模式以 OD 交通流矩阵呈现）。

要想形式化感染者扩散病毒的过程，我们需要基本传染数 R0。 R0 = β_t / γ，其中 γ 表示治愈率。截至本文写作时，2019-nCoV 的 R0 估计值在 1.4 到 4 之间。本文以最坏的情形为例，即 R0 值为 4。不过我们应该注意，这其实是个随机变量，报告的数字只是估计值。

本文尝试在每个地点用不同的 R0 值进行模拟，这些 R0 值采样自候选伽马分布，平均值为 4：

现在我们可以得到模型动态：

其中 β_k,t 表示第 t 天地点 k 处的（随机）传染率，α 系数表示城市公共交通使用率。

上式描述的模型动态非常简单：以第 t+1 天的地点 j 为例，我们需要从易感人群 S_j,t 中去除地点 j 处的感染者比例（第一个公式的第二项）以及从这座城市其他地方流入的感染者比例，其权重为传染率 β_k,t（第一个公式的第三项）。由于总人口 N_j = S_j + I_j + R_j，因此我们需要将刚才去除的部分移到感染组（第二个公式），将治愈者移到 R_j,t+1（第三个公式）。

模拟设置

为方便分析，本文以聚集的方式使用来自当地共乘公司 gg GPS 数据的日常 OD 交通流矩阵，并用它表示埃里温市的流动模式。接下来，我们需要每个 250×250m 网格单元中的人口数。我们通过按比例缩放提取到的 OD 交通流数量来逼近该数字，使不同地点的总流入量接近埃里温市总人口（110 万）的一半。这实际上是一次大胆的假设，但是由于对这部分做出更改仍会得到非常类似的结果，因此本文坚持使用该假设。

减少公共交通出行？

在第一次模拟中，假设可持续的公共交通主导城市未来流动，即 α=0.9：

从上图中，我们可以看到感染者比例立即攀升，在大约 8–10 天处达到峰值，将近 70% 的人口被感染，只有少量人口（约 10%）痊愈。到第 100 天病毒撤退时，治愈者比例达到令人震惊的 90%！

我们再来看，将公共交通的密度减少到 α = 0.2 对缓解流行病扩散是否有影响。这也可以解释为：采取有力措施来减少城市交通出行（如实行戒严），或增加私家车比例，以降低人口流动过程中的感染几率。

我们看到峰值在第 16-20 天到来，感染者比例要小得多（约 45%），治愈者比例是之前的 2 倍（约 20%）。到流行病结束时，易感人群比例是之前的 2 倍（大约 24% vs. 12%），这意味着更多人从该流行病的魔爪下逃脱。和预计的一样，采取有力措施暂时减少城市交通出行对疾病扩散情况有巨大影响。

隔离热门场所？

现在，我们来看另一个直观思路：完全隔离少数关键热门地区可以达到疾病控制预期。为此，本文选择了交通流量处于城市前 1% 的地点，并且完全阻止这些地点的人口流入和流出，有效地建立起隔离区。

从上图中可以看到，埃里温市的这些地点大部分位于市中心，还有两个是最大的购物中心。选择 α = 0.5，得到：

我们可以看到，峰值处的感染者比例更低（约 35%），最重要的是，在疫情结束时，大约一半的人口没有被感染！

下图展示了公共交通比例较高时的病毒传播态：

结论

本文并未执行精确的流行病建模（甚至对流行病学也仅具备基础的了解），而是为了粗略了解在传染病爆发时小世界网络效应对城市的影响。随着人口密度、流动性和活力的增长，城市更容易遭遇「黑天鹅事件」，也更加脆弱。

如果没有高效的危机处理能力和机制，城市再智能再可持续也都没有了意义。例如，我们看到在重点地区设置隔离区，或者采取强力措施控制人口流动，在卫生危机中能够起到重要作用。

当然，传染病的确切扩散机制仍是活跃的研究领域，未来我们可以看到更多利用数据进行模拟的方法。这种研究成果可以和城市规划、政策制定和管理整合，从而使城市更安全、更稳健。

上述模拟的代码如下所示：

import numpy as np
  # initialize the population vector from the origin-destination flow matrix
  N_k = np.abs(np.diagonal(OD) + OD.sum(axis=0) - OD.sum(axis=1))
  locs_len = len(N_k)                 # number of locations
  SIR = np.zeros(shape=(locs_len, 3)) # make a numpy array with 3 columns for keeping track of the S, I, R groups
  SIR[:,0] = N_k                      # initialize the S group with the respective populations

  first_infections = np.where(SIR[:, 0]<=thresh, SIR[:, 0]//20, 0)   # for demo purposes, randomly introduce infections
  SIR[:, 0] = SIR[:, 0] - first_infections
  SIR[:, 1] = SIR[:, 1] + first_infections                           # move infections to the I group

  # row normalize the SIR matrix for keeping track of group proportions
  row_sums = SIR.sum(axis=1)
  SIR_n = SIR / row_sums[:, np.newaxis]

  # initialize parameters
  beta = 1.6
  gamma = 0.04
  public_trans = 0.5                                 # alpha
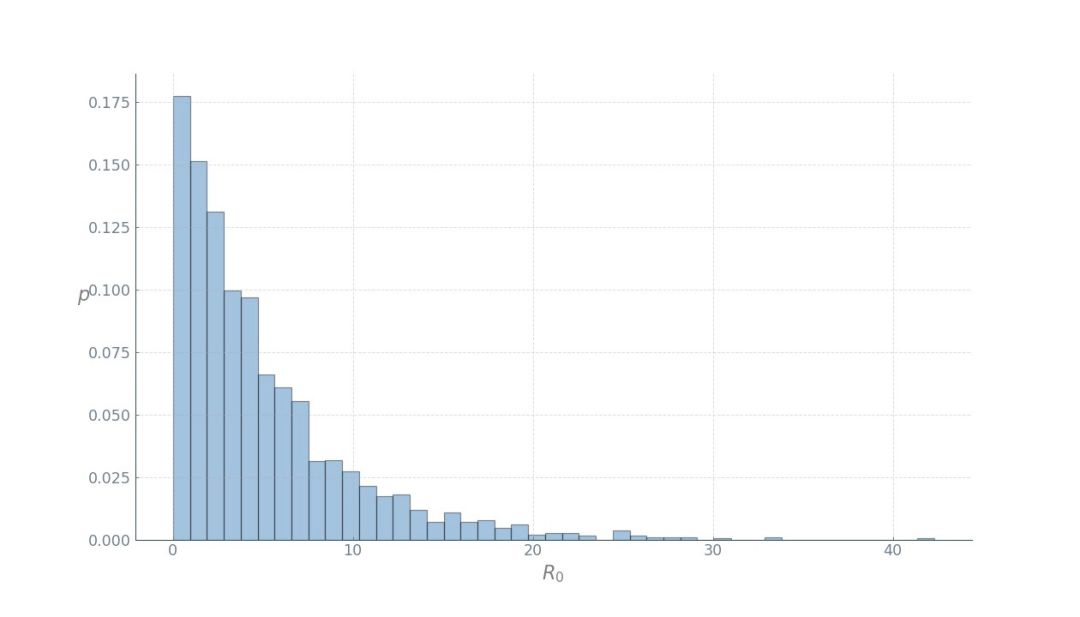
  R0 = beta/gamma
  beta_vec = np.random.gamma(1.6, 2, locs_len)
  gamma_vec = np.full(locs_len, gamma)
  public_trans_vec = np.full(locs_len, public_trans)

  # make copy of the SIR matrices 
  SIR_sim = SIR.copy()
  SIR_nsim = SIR_n.copy()

  # run model
  print(SIR_sim.sum(axis=0).sum() == N_k.sum())
  from tqdm import tqdm_notebook
  infected_pop_norm = []
  susceptible_pop_norm = []
  recovered_pop_norm = []
  for time_step in tqdm_notebook(range(100)):
      infected_mat = np.array([SIR_nsim[:,1],]*locs_len).transpose()
      OD_infected = np.round(OD*infected_mat)
      inflow_infected = OD_infected.sum(axis=0)
      inflow_infected = np.round(inflow_infected*public_trans_vec)
      print('total infected inflow: ', inflow_infected.sum())
      new_infect = beta_vec*SIR_sim[:, 0]*inflow_infected/(N_k + OD.sum(axis=0))
      new_recovered = gamma_vec*SIR_sim[:, 1]
      new_infect = np.where(new_infect>SIR_sim[:, 0], SIR_sim[:, 0], new_infect)
      SIR_sim[:, 0] = SIR_sim[:, 0] - new_infect
      SIR_sim[:, 1] = SIR_sim[:, 1] + new_infect - new_recovered
      SIR_sim[:, 2] = SIR_sim[:, 2] + new_recovered
      SIR_sim = np.where(SIR_sim<0,0,SIR_sim)
      # recompute the normalized SIR matrix
      row_sums = SIR_sim.sum(axis=1)
      SIR_nsim = SIR_sim / row_sums[:, np.newaxis]
      S = SIR_sim[:,0].sum()/N_k.sum()
      I = SIR_sim[:,1].sum()/N_k.sum()
      R = SIR_sim[:,2].sum()/N_k.sum()
      print(S, I, R, (S+I+R)*N_k.sum(), N_k.sum())
      print('\n')
      infected_pop_norm.append(I)
      susceptible_pop_norm.append(S)
      recovered_pop_norm.append(R)