教程 | 遗传算法的基本概念和实现（附Java实现案例）

选自Medium

作者：MallawaarachchiFollow

机器之心编译

参与：俞云开、蒋思源

基因遗传算法是一种灵感源于达尔文自然进化理论的启发式搜索算法。该算法反映了自然选择的过程，即最适者被选定繁殖，并产生下一代。本文简要地介绍了遗传算法的基本概念和实现，希望能为读者展示启发式搜索的魅力。

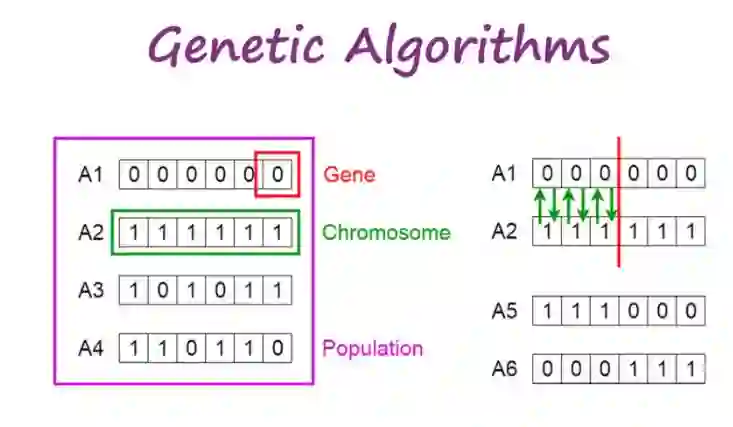
如上图（左）所示，遗传算法的个体由多条染色体组成，每条染色体由多个基因组成。上图（右）展示了染色体分割和组合的方式。

遗传算法的概念

自然选择的过程从选择群体中最适应环境的个体开始。后代继承了父母的特性，并且这些特性将添加到下一代中。如果父母具有更好的适应性，那么它们的后代将更易于存活。迭代地进行该自然选择的过程，最终，我们将得到由最适应环境的个体组成的一代。

这一概念可以被应用于搜索问题中。我们考虑一个问题的诸多解决方案，并从中搜寻出最佳方案。

遗传算法含以下五步：

1. 初始化
   

2. 个体评价（计算适应度函数）
   

3. 选择运算
   

4. 交叉运算
   

5. 变异运算

初始化

该过程从种群的一组个体开始，且每一个体都是待解决问题的一个候选解。

个体以一组参数（变量）为特征，这些特征被称为基因，串联这些基因就可以组成染色体（问题的解）。

在遗传算法中，单个个体的基因组以字符串的方式呈现，通常我们可以使用二进制（1 和 0 的字符串）编码，即一个二进制串代表一条染色体串。因此可以说我们将基因串或候选解的特征编码在染色体中。

种群、染色体和基因

个体评价（计算适应度函数）

个体评价利用适应度函数评估了该个体对环境的适应度（与其它个体竞争的能力）。每一个体都有适应度评分，个体被选中进行繁殖的可能性取决于其适应度评分。适应度函数值越大，解的质量就越高。适应度函数是遗传算法进化的驱动力，也是进行自然选择的唯一标准，它的设计应结合求解问题本身的要求而定。

选择运算

选择运算的目的是选出适应性最好的个体，并使它们将基因传到下一代中。基于其适应度评分，我们选择多对较优个体（父母）。适应度高的个体更易被选中繁殖，即将较优父母的基因传递到下一代。

交叉运算

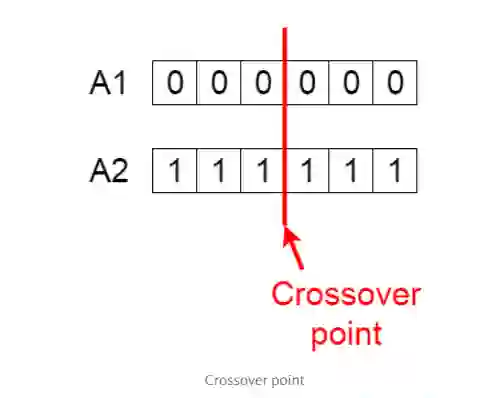
交叉运算是遗传算法中最重要的阶段。对每一对配对的父母，基因都存在随机选中的交叉点。

举个例子，下图的交叉点为 3：

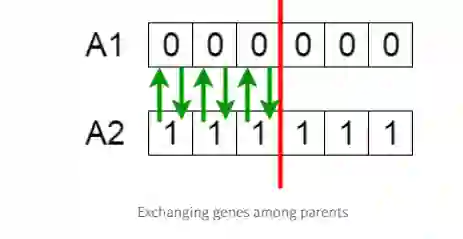
父母间在交叉点之前交换基因，从而产生了后代。

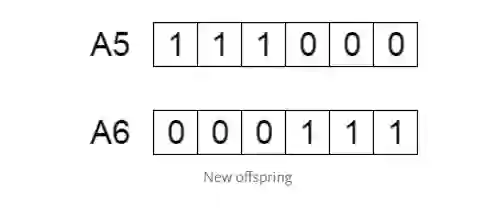
父母间交换基因，然后产生的新后代被添加到种群中。

变异运算

在某些形成的新后代中，它们的某些基因可能受到低概率变异因子的作用。这意味着二进制位串中的某些位可能会翻转。

变异运算前后

变异运算可用于保持种群内的多样性，并防止过早收敛。

终止

在群体收敛的情况下（群体内不产生与前一代差异较大的后代）该算法终止。也就是说遗传算法提供了一组问题的解。

案例实现

种群的规模恒定。新一代形成时，适应度最差的个体凋亡，为后代留出空间。这些阶段的序列被不断重复，以产生优于先前的新一代。

这一迭代过程的伪代码：

START
Generate the initial population
Compute fitness
REPEAT
    Selection
    Crossover
    Mutation
    Compute fitness
UNTIL population has converged
STOP

Java 中的实例实现

以下展示的是遗传算法在 Java 中的示例实现，我们可以随意调试和修改这些代码。给定一组五个基因，每一个基因可以保存一个二进制值 0 或 1。这里的适应度是基因组中 1 的数量。如果基因组内共有五个 1，则该个体适应度达到最大值。如果基因组内没有 1，那么个体的适应度达到最小值。该遗传算法希望最大化适应度，并提供适应度达到最大的个体所组成的群体。注意：本例中，在交叉运算与突变运算之后，适应度最低的个体被新的，适应度最高的后代所替代。

import java.util.Random;

/**
 *
 * @author Vijini
 */

//Main class
public class SimpleDemoGA {

    Population population = new Population();
    Individual fittest;
    Individual secondFittest;
    int generationCount = 0;

    public static void main(String[] args) {

        Random rn = new Random();
        
        SimpleDemoGA demo = new SimpleDemoGA();
        
        //Initialize population
        demo.population.initializePopulation(10);
        
        //Calculate fitness of each individual
        demo.population.calculateFitness();
        
        System.out.println("Generation: " + demo.generationCount + " Fittest: " + demo.population.fittest);

        //While population gets an individual with maximum fitness
        while (demo.population.fittest < 5) {
            ++demo.generationCount;
            
            //Do selection
            demo.selection();
            
            //Do crossover
            demo.crossover();
            
            //Do mutation under a random probability
            if (rn.nextInt()%7 < 5) {
                demo.mutation();
            }
            
            //Add fittest offspring to population
            demo.addFittestOffspring();
            
            //Calculate new fitness value 
            demo.population.calculateFitness();
            
            System.out.println("Generation: " + demo.generationCount + " Fittest: " + demo.population.fittest);
        }

        System.out.println("\nSolution found in generation " + demo.generationCount);
        System.out.println("Fitness: "+demo.population.getFittest().fitness);
        System.out.print("Genes: ");
        for (int i = 0; i < 5; i++) {
            System.out.print(demo.population.getFittest().genes[i]);
        }

        System.out.println("");

    }

    //Selection
    void selection() {
        
        //Select the most fittest individual
        fittest = population.getFittest();
        
        //Select the second most fittest individual
        secondFittest = population.getSecondFittest();
    }

    //Crossover
    void crossover() {
        Random rn = new Random();
        
        //Select a random crossover point
        int crossOverPoint = rn.nextInt(population.individuals[0].geneLength);

        //Swap values among parents
        for (int i = 0; i < crossOverPoint; i++) {
            int temp = fittest.genes[i];
            fittest.genes[i] = secondFittest.genes[i];
            secondFittest.genes[i] = temp;

        }

    }

    //Mutation
    void mutation() {
        Random rn = new Random();
        
        //Select a random mutation point
        int mutationPoint = rn.nextInt(population.individuals[0].geneLength);

        //Flip values at the mutation point
        if (fittest.genes[mutationPoint] == 0) {
            fittest.genes[mutationPoint] = 1;
        } else {
            fittest.genes[mutationPoint] = 0;
        }

        mutationPoint = rn.nextInt(population.individuals[0].geneLength);

        if (secondFittest.genes[mutationPoint] == 0) {
            secondFittest.genes[mutationPoint] = 1;
        } else {
            secondFittest.genes[mutationPoint] = 0;
        }
    }

    //Get fittest offspring
    Individual getFittestOffspring() {
        if (fittest.fitness > secondFittest.fitness) {
            return fittest;
        }
        return secondFittest;
    }


    //Replace least fittest individual from most fittest offspring
    void addFittestOffspring() {
        
        //Update fitness values of offspring
        fittest.calcFitness();
        secondFittest.calcFitness();
        
        //Get index of least fit individual
        int leastFittestIndex = population.getLeastFittestIndex();
        
        //Replace least fittest individual from most fittest offspring
        population.individuals[leastFittestIndex] = getFittestOffspring();
    }

}


//Individual class
class Individual {

    int fitness = 0;
    int[] genes = new int[5];
    int geneLength = 5;

    public Individual() {
        Random rn = new Random();

        //Set genes randomly for each individual
        for (int i = 0; i < genes.length; i++) {
            genes[i] = rn.nextInt() % 2;
        }

        fitness = 0;
    }

    //Calculate fitness
    public void calcFitness() {

        fitness = 0;
        for (int i = 0; i < 5; i++) {
            if (genes[i] == 1) {
                ++fitness;
            }
        }
    }

}

//Population class
class Population {

    int popSize = 10;
    Individual[] individuals = new Individual[10];
    int fittest = 0;

    //Initialize population
    public void initializePopulation(int size) {
        for (int i = 0; i < individuals.length; i++) {
            individuals[i] = new Individual();
        }
    }

    //Get the fittest individual
    public Individual getFittest() {
        int maxFit = Integer.MIN_VALUE;
        for (int i = 0; i < individuals.length; i++) {
            if (maxFit <= individuals[i].fitness) {
                maxFit = i;
            }
        }
        fittest = individuals[maxFit].fitness;
        return individuals[maxFit];
    }

    //Get the second most fittest individual
    public Individual getSecondFittest() {
        int maxFit1 = 0;
        int maxFit2 = 0;
        for (int i = 0; i < individuals.length; i++) {
            if (individuals[i].fitness > individuals[maxFit1].fitness) {
                maxFit2 = maxFit1;
                maxFit1 = i;
            } else if (individuals[i].fitness > individuals[maxFit2].fitness) {
                maxFit2 = i;
            }
        }
        return individuals[maxFit2];
    }

    //Get index of least fittest individual
    public int getLeastFittestIndex() {
        int minFit = 0;
        for (int i = 0; i < individuals.length; i++) {
            if (minFit >= individuals[i].fitness) {
                minFit = i;
            }
        }
        return minFit;
    }

    //Calculate fitness of each individual
    public void calculateFitness() {

        for (int i = 0; i < individuals.length; i++) {
            individuals[i].calcFitness();
        }
        getFittest();
    }

}

原文地址：https://medium.com/towards-data-science/introduction-to-genetic-algorithms-including-example-code-e396e98d8bf3

本文为机器之心编译，转载请联系本公众号获得授权。

✄------------------------------------------------

加入机器之心（全职记者/实习生）：hr@jiqizhixin.com

投稿或寻求报道：editor@jiqizhixin.com

广告&商务合作：bd@jiqizhixin.com

点击阅读原文，查看机器之心官网↓↓↓