纪念数学王子高斯诞辰242周年
节选自维基百科, [遇见数学] 有修改, 转载请注明.

约翰·卡尔·弗里德里希·高斯(德语:Johann Karl Friedrich Gauß,1777年4月30日-1855年2月23日), 德国数学家、物理学家、天文学家、大地测量学家,生于布伦瑞克,卒于哥廷根。高斯被认为是历史上最重要的数学家之一,并有“数学王子”的美誉。

上图为[遇见]为纪念高斯设计出来文化T恤内容, 具体可见今日第二篇文章
生平
高斯是一对普通夫妇的儿子。他的母亲是一个贫穷石匠的女儿,虽然十分聪明,但却没有接受过教育,近似于文盲。在她成为高斯父亲的第二个妻子之前,她从事女佣工作。他的父亲曾做过工头、商人的助手和一个小保险公司的评估师。高斯三岁时便能够纠正他父亲的借债帐目,这件事情已经成为一个轶事流传至今。他曾说,他能够在脑袋中进行复杂的计算。
据说高斯在9岁时,就发明了一个快速计算等差数列求和的小技巧,在很短的时间内计算完成了他的小学老师在黑板上给出的问题:计算从1到100这100个自然数之和。他所使用的方法是:将第1个数字与最后1个数字相加、第2个数字与倒数第2个数字相加……以此类推,可以得到50对101,于是101×50=5050便是答案。
小时候高斯家里很穷,且他父亲不认为学问有什么用,但高斯依旧喜欢看书,话说在小时候,冬天吃完饭后他父亲就会要他上床睡觉,以节省燃油,但当他上床睡觉时,他会将芜菁的内部挖空,里面塞入棉布卷,当成灯来使用,以继续读书。
当高斯12岁时,已经开始怀疑几何原本中的基础证明。当他16岁时,预测在欧氏几何之外必然会产生一门完全不同的几何学,即非欧几里德几何学。他导出了二项式定理的一般形式,将其成功的运用在无穷级数,并发展了数学分析的理论。

在高斯的出生地布伦瑞克的雕像(图自维基)
高斯的老师布吕特内尔与他的助手马丁·巴尔特斯很早就认识到了高斯在数学上的天赋,同时卡尔·威廉·斐迪南·冯·布伦瑞克也对这个天才儿童留下了深刻印象。于是他们从高斯14岁起便资助其学习与生活。这也使高斯能够在公元1792年进入Carolinum学院(今天布伦瑞克工业大学的前身)学习,并在那里开始对高等数学作研究:独立发现二项式定理的一般形式、数论上的“二次互反律”、素数定理、及算术-几何平均数。1795年,高斯转入哥廷根大学学习。1796年,19岁的高斯完成《正十七边形尺规作图之理论与方法》,成为第一位只用尺规作图成功画出正17边形的人。
1807年高斯成为哥廷根大学的教授和当地天文台的台长。
尽管高斯作为一个数学家而闻名于世,但这并不意味着他热爱教书。尽管如此,他越来越多的学生成为有影响的数学家,如后来闻名于世的戴德金和黎曼。
1855年2月23日凌晨一时许,77岁的高斯因心脏病发作,在哥廷根天文台的躺椅上去世。
重大贡献
18岁的高斯发现了最小二乘法,并猜测了质数定理。通过对足够多的测量数据的处理后,可以得到一个新的、概率性质的测量结果。在这些基础之上,高斯随后专注于曲面与曲线的计算,并成功得到高斯钟形曲线(正态分布曲线)。其函数被命名为标准正态分布(或高斯分布),并在概率计算中大量使用。
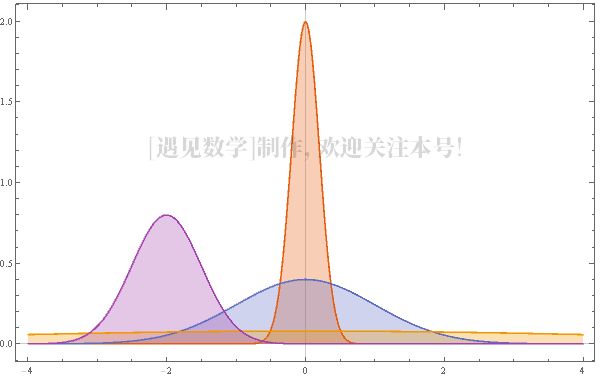
4种参数不同下的正态分布
在高斯19岁时,仅用尺规便构造出了17边形。并为流传了2000年的欧氏几何提供了自古希腊时代以来的第一次重要补充。
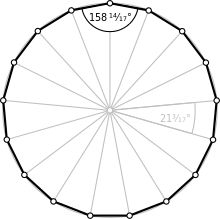
高斯总结了复数的应用,并且严格证明了每一个n阶的代数方程必有n个实数或者复数解。1801年[10],在他的第一本著名的著作《算术研究》中,作出了二次互反律的证明,成为数论继续发展的重要基础。在这部著作的第一章,导出了全等三角形定理的概念。
高斯在最小二乘法基础上创立的测量平差理论的帮助下,测算天体的运行轨迹。他用这种方法,测算出了小行星谷神星的运行轨迹。
谷神星于1801年被意大利天文学家皮亚齐发现,但因病他耽误了观测,从而失去了这颗小行星的轨迹。皮亚齐以希腊神话中的“丰收女神”对它命名,称为谷神星,并将自己以前观测的数据发表出来,希望全球的天文学家一起寻找。高斯通过以前3次的观测数据,计算出了谷神星的运行轨迹。奥地利天文学家海因里希·欧伯斯根据高斯计算出的轨道成功地发现了谷神星。高斯将这种方法发表在其著作《天体运动论》中。

1838年出版的天文学通报中高斯肖像。(图自维基)
为了获知每年复活节的日期,高斯推导了复活节日期的计算公式。他的母亲是文盲,从未记录他出生的日期,只记得他出生于耶稣升天节前八天的一个星期三(复活节后第三十九天)。 高斯后来在找到复活节的日期的情况下解决了关于他出生日期的这个难题,并且继而推导出计算过去和未来年份复活节日期的方法。
1818年至1826年间,高斯主导了汉诺威公国的大地测量工作。通过最小二乘法为基础的测量平差的方法和求解线性方程组的方法,显著地提高了测量的精度。
高斯亲自参加野外测量工作。他白天观测,夜晚计算。在五六年间,经他亲自计算过的大地测量数据超过100万个。当高斯领导的三角测量外场观测走上正轨后,高斯把主要精力转移到处理观测成果的计算上,写出了近20篇对现代大地测量学具有重大意义的论文。在这些论文中,他推导了由椭圆面向圆球面投影时的公式,并作出了详细证明。这个理论直至现在仍有应用的价值。
汉诺威公国的大地测量工作至1848年结束。这项大地测量史上的巨大工程,如果没有高斯在理论上的仔细推敲,在观测上力图合理和精确,在数据处理上尽量周密和细致,就不能圆满的完成。在当时的不发达的条件下,布设了大规模的大地控制网,精确地确定2578个三角点的大地坐标。
为了用椭圆在球面上的正形投影理论以解决大地测量中出现的问题,在这段时间内高斯亦从事了曲面和投影的理论,并成为了微分几何的重要理论基础。相对论证明了宇宙空间实际上是非欧几何的空间。高斯的思想被近100年后的物理学所认可。
高斯试图在汉诺威公国的大地测量中通过测量Harz的Brocken——Thuringer Wald的Inselsberg——哥廷根的Hohen Hagen三个山头所构成的三角形的内角和,以验证非欧几何的正确性,但未成功。高斯的朋友鲍耶的儿子雅诺斯在1823年证明了非欧几何的存在,高斯对他勇于探索的精神表示了赞扬。1840年,罗巴切夫斯基用德文写了《平行线理论的几何研究》一文。这篇论文的发表引起了高斯的注意。他非常重视这一论证,积极建议哥廷根大学聘请罗巴切夫斯基为通信院士。为了能直接阅读他的著作,从这一年开始,63岁的高斯开始学习俄语,并最终掌握了这门外语。高斯最终成为微分几何的始祖(高斯、雅诺斯和罗巴切夫斯基)之一。
出于对实际应用的兴趣,高斯发明了日光反射仪。日光反射仪可以将光束反射至大约450公里外的地方。高斯后来不止一次地为原先的设计作出改进,试制成功了后来被广泛应用于大地测量的镜式六分仪。
19世纪30年代,高斯发明了磁强计。他辞去了天文台的工作,而转向物理的研究。他与威廉·韦伯(1804-1891)在电磁学领域共同工作。他比韦伯年长27岁,以亦师亦友的身份与其合作。1833年,通过受电磁影响的罗盘指针,他向韦伯发送出电报。这不仅是从韦伯的实验室与天文台之间的第一个电话电报系统,也是世界首创的第一个电话电报系统。
1840年,他和韦伯画出了世界第一张地球磁场图,并且定出了地球磁南极和磁北极的位置。次年,这些位置得到美国科学家的证实。
高斯在数个领域进行研究,但只把他认为已经成熟的理论发表出来。他经常对他的同事表示,该同事的结论自己以前已经证明过了,只是因为基础理论的不完备而没有发表。事实上高斯把他的研究结果都记录了起来。他死后,他的20部纪录着他的研究结果和想法的笔记被发现,证明高斯所说的是事实。一般人认为,20部笔记并非高斯笔记的全部。
纪念活动
从1989年直到2001年年底,他的肖像和他所发现的正态分布曲线与一些在哥廷根突出的建筑物,一起被放入德国10马克的钞票中。另一方面,在汉诺威有和他有关的鸡血石以及三角测量方法。在德国也发行了三种用以表彰高斯的邮票。第一种邮票(第725号)发行于1955年−他死后的第100周年;另外两种邮票(第1246号.第1811号)发行于1977年,他出生的第200周年。

在高斯的荣耀中,以他命名的事物包括:
用在磁场的CGS制计量单位以高斯来命名。
月球上的坑洞以他来命名。
小行星1001又称为“高斯星”。
一艘名为“高斯”的船,是高斯远征南极时所使用的船。
相关文章或视频
» 文章 | 为什么高斯选择成为一位数学家?| 数学万花筒
» 动画 | 数学王子高斯
» 视频 | 代数基本定理
» 文章 | 【从高斯算1+2+3+...+100 谈起】
» 文章 | 【数学王子 - 高斯】纪念诞辰240周年





