【TPAMI2021】鲁棒可微SVD，Robust Differentiable SVD

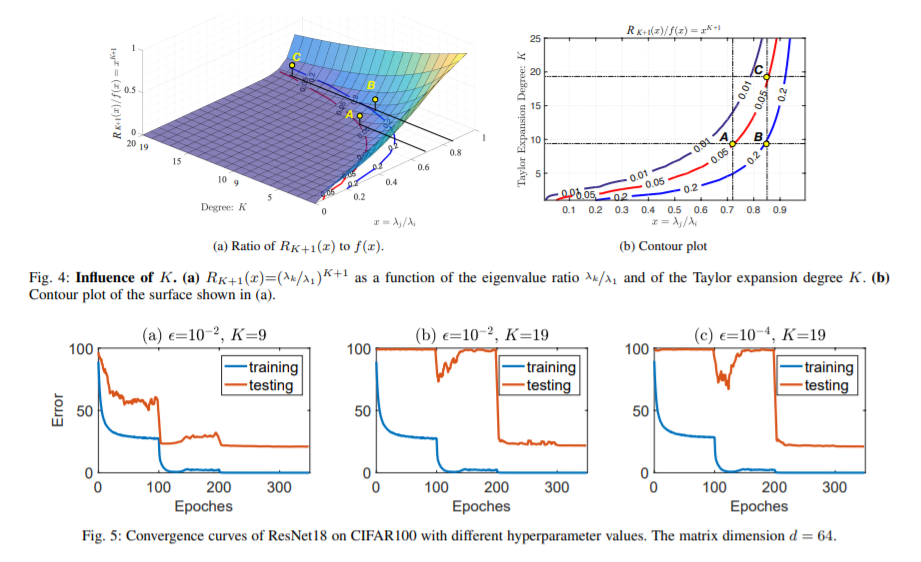
对称矩阵的特征分解是许多计算机视觉算法的核心。然而，特征向量的导数往往是数值不稳定的，无论是使用SVD来解析计算它们，还是使用幂迭代(PI)方法来近似它们。这种不稳定性出现在特征值彼此接近的情况下。这使得将特征分解集成到深度网络中变得困难，而且往往导致收敛性较差，特别是在处理大型矩阵时。虽然这可以通过将数据分割成任意的小组来缓解，但这样做没有理论基础，而且不可能充分利用特征分解的能力。在之前的工作中，我们在前向通过期间使用SVD和PI来计算后向通过期间的梯度来缓解这一问题。然而，使用PI计算多个特征向量所需的迭代压缩过程往往会累积误差，产生不准确的梯度。在这里，我们证明了SVD梯度的泰勒展开在理论上等价于使用PI得到的梯度，而在实践中不依赖于迭代过程，因此得到了更精确的梯度。我们将此对于提高图像分类和样式转换精度的好处。

https://www.zhuanzhi.ai/paper/cd172c7853be3e6b782fe28a8210ba8f

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“RDSVD” 就可以获取《【TPAMI2021】鲁棒可微SVD，Robust Differentiable SVD》专知下载链接

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源