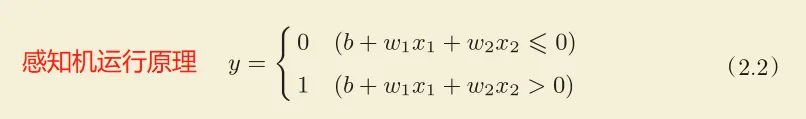豆瓣9.4！《深度学习入门》笔记总结，带你从感知机入门深度学习！（连载）

作者 ： 云不见

链接 ：https://blog.csdn.net/Walk_OnTheRoad/article/details/107700703

此笔记是基于《深度学习入门》这本书的重点知识汇总。

本文重点知识点：

• 感知机/多层感知机MLP
  

• NumPy多维数组的运算部分总结

• 正向传播（正向传播算法，也叫前向传播算法）

• 激活函数

• 损失函数

目录：

1、感知机/多层感知机（MLP）

2、NumPy多维数组的运算

3、前向传播（forward propagation）

4、激活函数

    （1）阶跃函数

    （2）sigmoid(逻辑回归常用)

    （3）ReLU函数（线性整流函数：最近使用的激活函数）（Rectified Linear Unit）

    （4）softmax函数（一般用于多元分类问题）

5、损失函数

    定义

    （1）均方误差

    （2）交叉熵误差

    （3）mini-batch版交叉熵误差的实现

    为何要设定损失函数？

1、感知机/多层感知机（MLP）

感知机是什么？

多个输入，一个输出。改变权重w可以实现与、与非和或门。(构造相同，只是权重参数不一样)

图1-1 感知机原理（用的激活函数是阶跃函数）

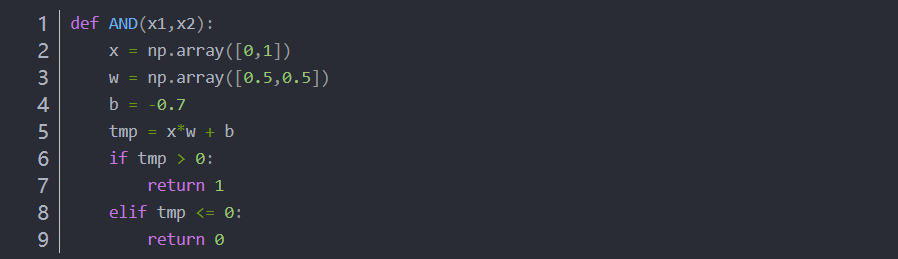
1.1  用感知机原理实现一个与门

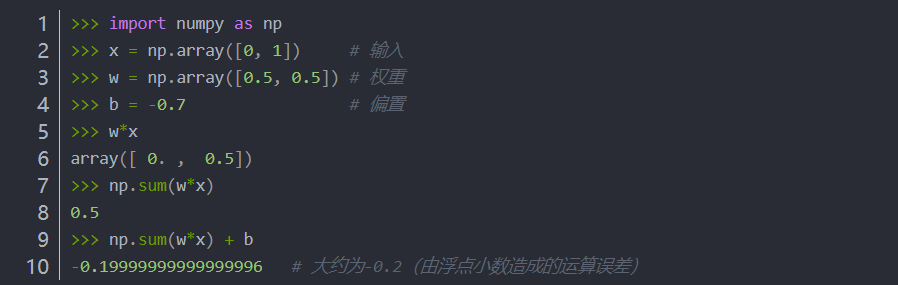
1.2  用 -b 代替 θ，用NumPy实现感知机

单层感知机的缺点：

• 不能实现异或门（因为没有这样的w和b参数存在）

• 为什么不能实现 ？

• 单层感知机只能表示由一条直线分割的空间，这种空间为线性空间；而异或是非线性的，空间不能由直线分割，不过可由曲线分割，这种空间为非线性空间

如何改进：叠加层。

• 引出多层感知机（MLP）

其实异或门可由 与、与非、或门 组合而成。所以异或是多层结构的神经网络（两层）。（一层不行，咱就叠加层）（一顿火锅解决不了，咱就再来一顿！）

而且两层感知机运作过程好比流水线作业，一层层传递

总结：单层感知机（线性）通过叠加层可进行非线性的表示

• 单层感知机——表示线性空间
  

• 多层感知机——表示非线性空间，理论上还可表示计算机

多层感知机 = 神经网络

感知机与神经网络的区别：激活函数不同！

• 单层感知机：激活函数为阶跃函数

• 神经网络：激活函数不是阶跃函数

2、NumPy多维数组的运算

np.ndim(A) ：获取数组的维数，维数由最小的行或者列来确定

A.shape ：获取数组的形状（几行几列），返回元组（tuple）

A.shape[0] 代表第一个维度，即行；
A.shape[1] 代表第二个维度，即列

二维数组 = 矩阵
比如：
A = [[1,2],
[3,4],
[5,6]]

行 = 第一个维度（第0维） = A.shape[0] = 有三个元素（有三行）
列 = 第二个维度（第1维） = A.shape[1] = 有两个元素（有两列）

np.dot()：矩阵乘法
接收两个NumPy数组作为参数，并返回数组的乘积。

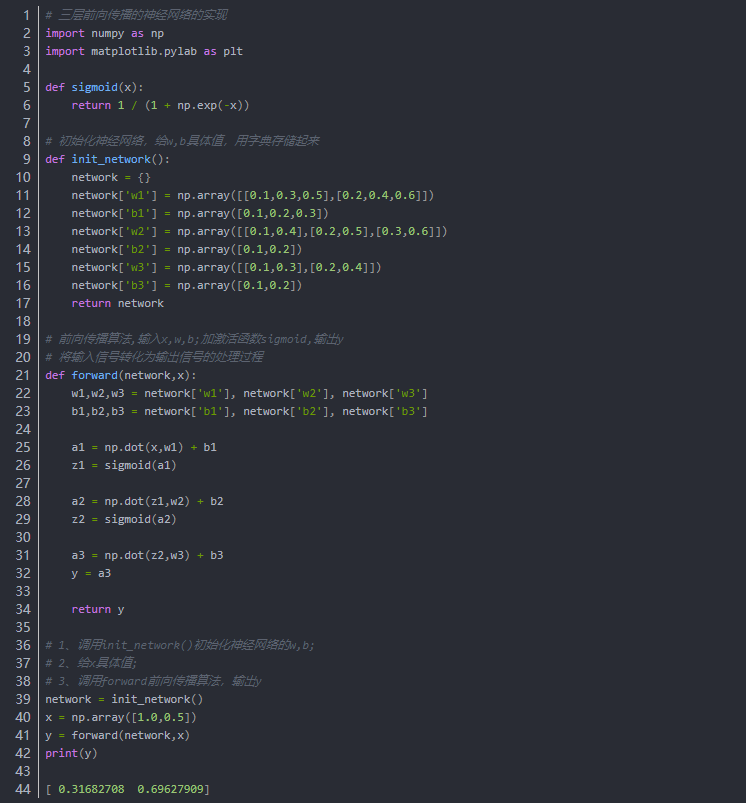
3、前向传播（forward propagation）

前向传播的实现（即假设已经知道了参数的值，进行分类任务）
= 假设我们已经学习到了参数，进行推理任务，也就是对输入数据进行分类，这就是前向传播的过程。
即 前向传播 = 此处的推理处理

三层前向传播的神经网络的实现

4、激活函数

《深度学习入门》：一般而言，回归问题用恒等函数，分类问题用softmax函数。

感知机就是用的阶跃函数去激活的，那么用其他激活函数的就是神经网络了！

（1）阶跃函数

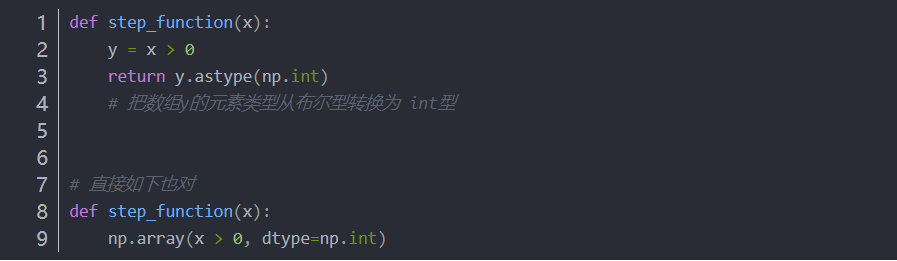
4.1.1  Python实现阶跃函数

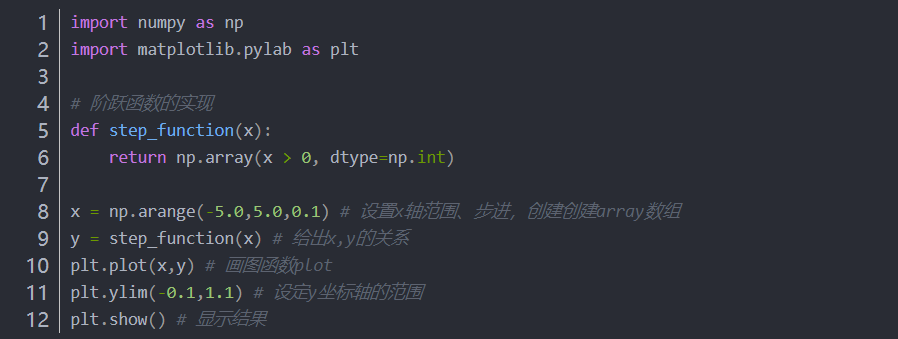
4.1.2  用NumPy实现阶跃函数(输入为正，输出1；输入为负，输出0)

4.1.3  画出阶跃函数

（2）sigmoid(逻辑回归常用)

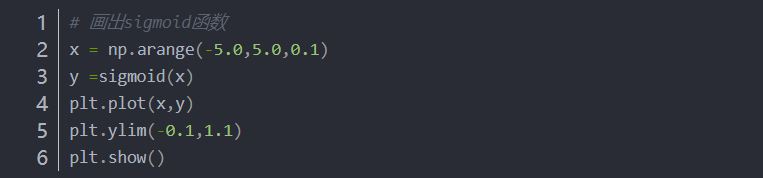
4.2.1  sigmoid函数的实现

4.2.2  画出sigmoid函数

sigmoid函数的平滑性对神经网络的学习具有重要意义。

（3）ReLU函数（线性整流函数：最近使用的激活函数）（Rectified Linear Unit）

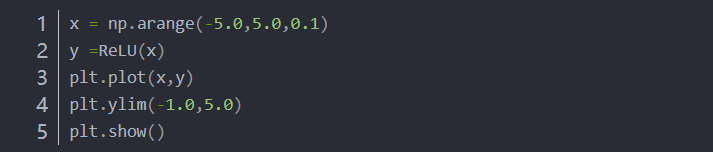
4.3.1  ReLU函数的实现

4.3.2  画出ReLU函数

输出层使用的激活函数选择要根据求解问题的性质决定。
回归问题：用恒等函数，直接输出
分类问题：
二元分类问题：用sigmoid函数
多元分类问题：用softmax函数（下次讨论）

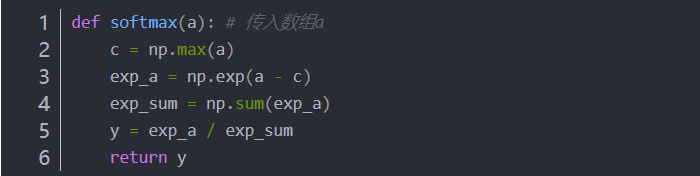
（4）softmax函数（一般用于多元分类问题）

softmax函数实现

softmax激活函数实现，一般用于多元分类

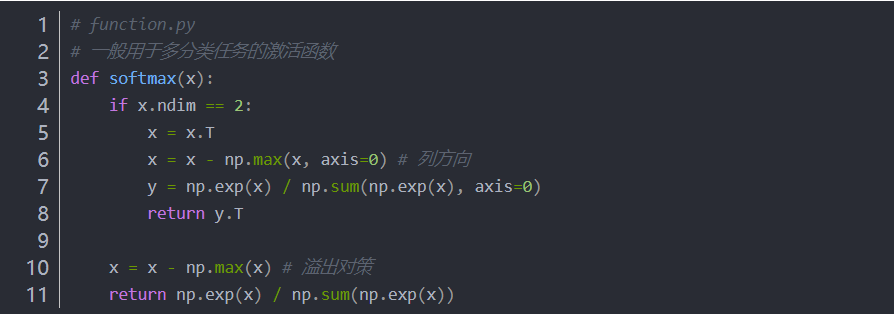
遇到指数函数要当心

防止溢出，加个或减去个C，结果不变

softmax激活函数改善，防止溢出，加个或减去个C

softmax函数的输出值的总和是1，所以可以把softmax函数的输出解释为“概率”。

axis = 1 行方向
axis = 0 列方向
注意：矩阵的第0维是列方向，第1维是行方向。——译者注

比如：
参数 axis=1。这指定了在100 × 10的数组中，沿着第1维方向（以第1维为轴）找到值最大的元素的索引（第0维对应第1个维度）

5、损失函数

定义

• 损失函数是表示神经网络性能的“有多坏（恶劣程度）”的指标，即当前的神经网络对监督数据（训练数据）在多大程度上不拟合，在多大程度上不一致。恶劣程度越小，越好。

• 神经网络以某个指标作为线索寻找最优权重参数，这个指标就是 损失函数（loss function）

• 损失函数一般用均方误差和交叉熵误差等。

• 当使用sigmoid作为激活函数的时候，常用交叉熵损失函数而不用均方误差损失函数。

（1）均方误差

python实现均方误差

（2）交叉熵误差

python实现交叉熵误差

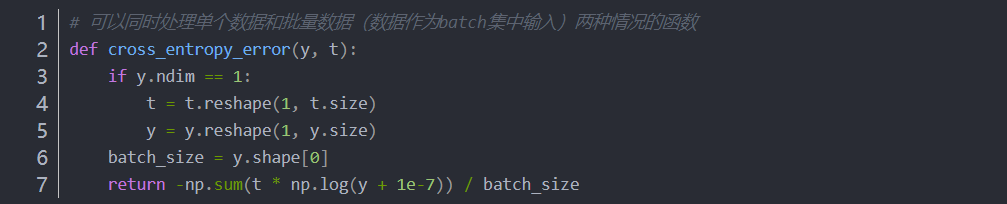
（3）mini-batch版交叉熵误差的实现

• 用随机选择的小批量数据（mini-batch）作为全体训练数据的近似值。（就像抽样、采样进行人口普查一样）

• 当监督数据 t 是标签形式（非one-hot表示，而是像“2”“7”这样的标签）时，交叉熵误差可通过如下代码实现

为何要设定损失函数？

• 我们的目标是获得使识别精度尽可能高的神经网络，那可以用识别精度作为指标吗？

• 为了找到使损失函数的值尽可能小的地方，需要计算参数的导数（梯度），以这个导数为指引，逐步更新参数的值。

• 如果导数的值为负，通过使该权重参数向正方向改变，减小损失函数的值；

• 如果导数的值为正，则通过使该权重参数向负方向改变，减小损失函数的值。

• 当导数的值为0时，无论权重参数向哪个方向变化，损失函数的值都不会改变，此时该权重参数的更新会停在此处。

• 那么如果以识别精度为指标，则参数的导数在绝大多数地方都会变为0。则无法更新参数。

• 综上，需要设定损失函数来描述神经网络的好坏。

欢迎关注【深度学习冲鸭】公众号，我会在这里记录自己在路上的一点一滴！

再小的人也有自己的品牌！期待和你一起进步！

立一个小小flag🚩2020年坚持20：20发文，大家准时来监督吧！！