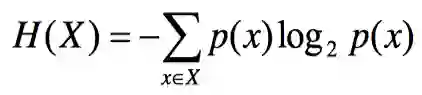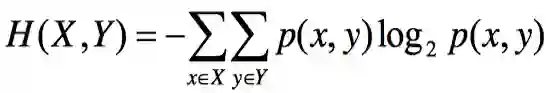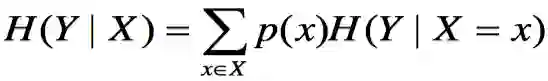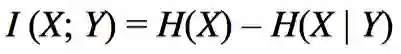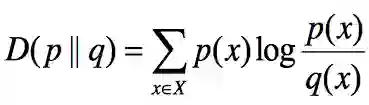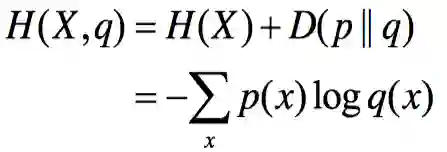基础 | 绕开数学，讲讲信息论

本文转自公众号：夕小瑶的卖萌屋

学过机器学习的人肯定知道很多决策树的核心就是计算信息论中的熵，自然语言处理（NLP）中的信息论更是无处不在。

但是很多人抱怨“各种XX熵，各种XX信息，全都是数学公式，只会生搬硬套，却完全不知道有什么意义，也完全不知道怎么用嘛~”好咯，下面就带你逐个击破！

熵/自信息

熵又称为自信息(self-information)，在通信系统中表示信源每发一个符号(不论发什么符号)时所提供的平均信息量。同时，熵也可以被视为描述一个事件/随机变量的不确定性的大小，一个事件/随机变量的熵越大，那么它的不确定性就越大，因此正确估计该事件/随机变量的值的可能性就越小。

随机变量可以简单理解为取值按照某种规律，随时间随机变化的变量。

 

上面这段话看似很乱，其实要核心意思就是用“熵”可以描述一个事件/随机变量的信息量！而越稀有的东西，发生的可能性越小的事件，所包含的信息量越大。

其实很好理解呀。你想想，对于一个发生的可能性很大的事件，比如一个人告诉你明天太阳从西边出来。那么你肯定会用关爱傻子的眼神看他。但是如果一个人告诉你明天这里要发生大地震！那你要是不跳起来的话说明你的心理素质真是蛮好的。所以说呀，一个小概率事件会携带特别多的信息量，而太大的信息量会让人受不了的。

哦对了，熵的单位是比特（bit），所以熵越大的事件/随机变量就要花越多的比特来表示咯。

 

在NLP领域有个好玩的计算就是对各种语言的熵进行计算。结果1989年的时候对英语字母的熵进行计算的结果是4.03（比特），而汉字的熵高达9.71（比特）！这说明了什么呢？

从直观的结果来看，表示一个汉字所需要的内存空间要比表示一个英文字母所需的空间大的多（想象一下ASCII码足以容纳全部英语字母，而常用汉字都远远的容不下）。从更深层的角度看，也说明我们对字母序列（比如单词）进行预测的难度要比对汉字序列（比如词语、成语）进行预测的难度大很多！因为汉字的不确定性，也就是熵，太大了！

高能公式：

联合熵

联合熵就是描述一对事件/一对随机变量平均需要的信息量。注意这里说的是一对！也就是两个！你可能想说“描述两个事件的信息量，直接对两个事件的信息量相加再除以2不就行了嘛~搞这么多稀奇古怪的定义干嘛呢”

 

这位童鞋，请再深入的想一下！假如这里有两个事件，一个事件是“明天你家后面的那个火山会爆发！”，这个事件包含1000bits的信息量。另一个事件是“明天你的豪宅就会被火山熔浆给融化了！”，这个事件包含1200bits的信息量。

 

那么如果告诉了你第一个事件，你很惊讶，你被砸了1000bits的信息量。这时再告诉你第二个事件，那么你还会再次惊讶吗？当然不会啦，你只会惊讶一次。因此第二次被砸的信息量远小于1200bits。但是如果把这两个事件分别告诉两个人，那么他们肯定都会特别惊讶，因此一共惊讶两次。为什么会这样呢？就是因为这两个事件的联合起来的信息量，即联合熵，并不是简单的相加的关系。专业的说法是这两个事件并不是相互独立的。

高能公式：

条件熵

理解了联合熵，条件熵就好理解啦~条件熵就是已知一个事件发生的情况下，另一个事件的信息量。回想刚才的火山的例子，已知“火山喷发”的情况下，“豪宅要被熔浆融化”的信息量就不大了。但单独的一个“豪宅要被熔浆融化”的信息量可是爆表的呀。

高能公式：

互信息

互信息也是说两个事件/随机变量之间的事儿。X与Y的互信息就是X的自信息（熵）减去【已知X的情况下，Y的条件熵】。直白的讲就是知道了X的值以后，Y的值的不确定性会降低多少。也就是说X的值会透露多少关于Y的信息量。

 

比如我们可以用互信息来分词。根据互信息的定义，当两个汉字的互信息越大时，表示这两个字的结合越紧密，因此这两个汉字越可能组合成词。因此我们只要计算出一个句子中前后两个字之间的互信息，不就可以轻松分词了嘛~（小夕偷偷告诉你，效果并不好

高能公式：

相对熵

相对熵（也称KL距离）用来描述两个事件的相近程度，或者说衡量两个随机分布的差距。当两个随机分布完全相同时，相对熵为0。两个随机分布差别越大，相对熵也越大。

 

想象一下，虽然前文的“火山爆发”与“熔浆融化豪宅”这两个事件互推的条件熵很小，但是这两个事件的含义却差别很大，因此它们的相对熵计算出来也会比较大。但是“明天火山爆发”与“明天下午两点火山喷发”的相对熵就会很小，因为它们几乎是同一个事件。

高能公式：

交叉熵

交叉熵的理解要抽象一些，它衡量的是一个估计的分布(模型)与真实概率分布之间的差异。

 

举个小例子解释，我们要设计语言模型来接近最真实的语言。语言模型越接近真实语言，那么通过该模型我们就很容易产生人类容易理解的句子、对话等，此时我们就可以说该语言模型的交叉熵很小。

 

但是如果你设计了一个语言模型，这个模型产生了“大极少上考虑”这种奇怪的句子，不符合真实的语言，因此就说你的语言模型交叉熵很大。

 

当然啦，实际上在描述语言模型时，一般不说交叉熵，而是说“困惑度”。虽然两者的数学形式略有不同，但本质上是一样的东西。

高能公式：

推荐阅读

基础 | TreeLSTM Sentiment Classification

基础 | 详解依存树的来龙去脉及用法

基础 | 基于注意力机制的seq2seq网络

原创 | Simple Recurrent Unit For Sentence Classification

原创 | Attention Modeling for Targeted Sentiment

原创 | cw2vec理论及其实现

基础 | 中英文词向量评测理论与实践

欢迎关注交流