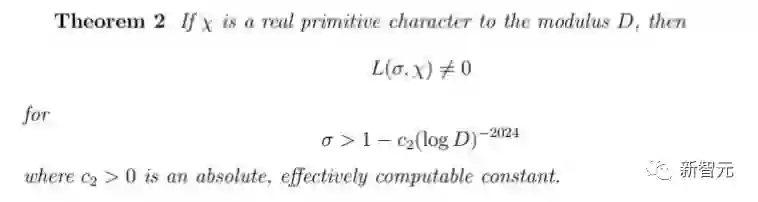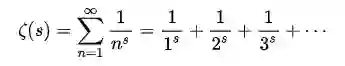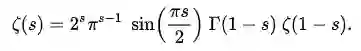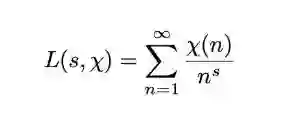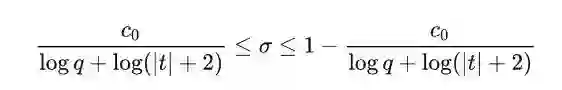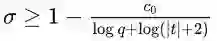昨天,著名华裔数学家张益唐教授在攻克数学界著名难题之一——郎道-西格尔零点猜想问题的道路上再进一步!
目前,解决这个零点猜想问题的111页的完整版预印本论文「Discrete mean estimates and the Landau-Siegel zero」已经可以下载。
https://pan.baidu.com/s/1GM61FrLynSfpSn67SoaHow?pwd=1105
上个月,张益唐教授在北京大学大纽约地区校友会举办的一次在线学术活动上透露,已解决郎道-西格尔零点猜想(Landau-Siegel zeros conjecture)问题,立即引发数学界广泛关注。
昨天,张益唐在山东大学的一次在线报告中简要介绍了这一成果。另外,他还将于11月8日在北大做《关于朗道-西格尔零点猜想》的在线报告。
据澎湃新闻报道,北京国际数学研究中心主任、北京大学数学英才班委员会主任田刚院士证实,张益唐有关朗道-西格尔零点猜想的新论文已完成并已提交至预印本网站Arxiv,预计下周一将正式上线。
张益唐教授研究的这个猜想,跟数学史上的另一个伟大问题——黎曼猜想有关,后者是数学家波恩哈德·黎曼于1859年提出,关于黎曼ζ函数ζ(s)的零点分布的猜想,是百年来的一大数学难题。
据《中国科学报》今年10月的介绍:简单来讲,如果存在朗道-西格尔零点,那么黎曼猜想就是错的;如果朗道-西格尔零点不存在,则不会和黎曼猜想发生冲突。
张益唐的同事、数论学家Stopple曾说,如果张益唐能对朗道-西格尔零点作出证明,加上他的上一份成就,在某种意义上,(其概率)就像是「同一个人被闪电劈中两次」。
「即使他从未成名,做出这项工作也会让他跟上次一样,被世界瞩目。」Stopple说。
Stopple说的「上一次成就」,是张益唐2013年在《数学年刊》发表《质数间的有界间隔》,证明了存在无穷多对质数间隙都小于7000万,在孪生素数猜想这一数论重大难题上取得了里程碑式的突破。
在看论文之前,首先咱们来看看,朗道—西格尔零点到底是什么。
朗道-西格尔零点猜想,是黎曼猜想的弱一些的形式。数学家们为了研究素数分布,引入了黎曼猜想。
1859年,德国数学家黎曼在论文「论小于给定数值的素数个数」中,首次提及这个猜想。
比某个特定数值要小的质数有多少个?质数在整个数列中的分布情况又是如何?
黎曼发现,质数的分布跟某个函数有着密切关系:
![]()
这个公式中,s是复数,可以写成s=a+bi这样的形式(a是s的实部、b是s的虚部、i则是根号负一)。
当s的实部小于1时,整个级数和可能会发散。为了让函数适用于更广的范围,黎曼把上面的ζ函数改写为:
![]()
当s为负偶数(s= -2, -4, -6…)时,黎曼ζ函数为零。这些s的值,就称为平凡零点。
不过,此外还有另一些s的值,能够让黎曼ζ函数为零,它们被称为非平凡零点。就是这些非平凡零点,对质数的分布有着决定性影响。
到了这里,黎曼本人也无法证明了。不过他做了一个猜测:黎曼ζ函数所有非平凡零点的实部都是二分之一,或者说黎曼ζ函数在1/2<x<1这一区域内没有零点。这就是黎曼猜想。
随后的数学家们,在前人的基础上继续前进。
数学家Dirichlet引入了狄利克雷L函数。
![]()
对于这个函数,也有一个猜想:狄利克雷L函数在1/2<x<1这一区域内没有零点。这就是广义黎曼猜想。
可以证明,L函数在σ=1时没有零点,因而可以证明等差数列上的素数定理。
但数学家们希望继续缩减L函数的非平凡零点的存在区域。有人证明出,L函数的非平凡零点基本上都能落在下面公式中的区域:
![]()
如果所有非平凡零点都满足,就可以证明带余项的等差数列素数定理。
但是朗道发现,当X满足特殊性质时,其对应的L函数可能会出现落在上面公式之外的异常零点。
不过朗道缩小了范围,他证明了L函数在下面这个区域中最多只有一个零点,而且这个零点一定是实数,阶数只能是1。这个零点就被称为西格尔零点。
![]()
数学家们希望证明的是,西格尔零点不存在,这就是朗道-西格尔零点猜想。
如果能够证明朗道-西格尔零点猜想,那么数论研究中的很多问题就不必再排除西格尔零点。
而张益唐的研究,就在极大范围内排除了朗道—西格尔零点的存在。
在10月15日北大校友线上会议上,张益唐这样说:「虽然是一个弱一点的形式,但本质上已经是解决了朗道—西格尔零点问题。」
此言一出,就引发了数学圈的大地震。如果他证明了朗道-西格尔零点存在,那么黎曼猜想就完全被否定了,这种可能性太小,因此大家当时的猜测是,张益唐要证明的应该是是朗道-西格尔零点不存在。
这篇论文结果意义重大,它使得以前的很多结果从假设性结果变成了确定性结果。
据澎湃新闻援引一位数论学者的解释,以往的很多论文,要假设朗道-西格尔零点猜想成立(也即假设西格尔零点不存在)。
换句话说,这次张益唐的新论文虽然没有排除掉西格尔零点存在的可能性,但其排除掉的范围足够涵盖很多以往论文所需的范围。
![]()
早在2007年5月,张益唐就曾在预印本网站arxiv提交了一篇标题为《论朗道-西格尔零点猜想》(On the Landau-Siegel Zeros Conjecture)论文,但里面的论证有些地方尚需完善。
https://arxiv.org/pdf/0705.4306.pdf
这次的新论文,在很大程度上完善和补充了2007版论文的结论和成果。
根据知乎答主「gujurat」的介绍,这次张益唐论文的主要成果,首先是L函数在1点处的下界估计,下界从D的负方幂改进到log D的负方幂。
其次是有关于实轴上非零区域的直接推论,常数是effecitive,说明方法上有本质变化。
相比于张益唐教授2007年发布的一版论文,这次可谓对07版的一次修补,论文也从07年版的54页扩到现在2022年版的111页。
如果要完整证明LS零点不存在,需要Theorem 2里面指数取到-1,所以现阶段还没有「完整」解决LS零点猜想。
在论文最后,张教授也表示Theorem 1里的指数-2022可能取到更大的负数值,但很难取到-1。
总的来说,完整解决郎道-西格尔零点猜想,无论是证明还是证否,都太过超前。
好消息是,从论文成果来看,张教授的最新论文比07年的版本有革命性的改进,至于论文究竟能取得多大的进展,还得等专业人士审稿之后才能确定。
2019年,在香港中文大学举办的「大师讲堂」上,张益唐介绍了朗道-西格尔零点问题的历史和应用,并解释为何这个问题这么重要,并且难以解决。
根据香港中文大学(深圳)整理的资料,张益唐本人是这样介绍的:
不过,目前很快即将发表的Arxiv预印本论文,距离正式登上数学界顶刊发表,尚待同行评议。
之前分析这篇论文意义的数论学者认为,这个评议过程可能会持续几个月。
论文从2007年版的54页,扩到现在2022年版的111页,审稿会是一个大工作。像这种论文,即使是顶尖的专业人士,把论文全部细节推一遍也得几个月。
11月8日,张益唐将会面向北大师生专门做一场学术报告,B站会有同步直播,感兴趣的小伙伴可以关注起来。
图源:北京大学数学科学学院官网
https://www.zhihu.com/question/564799818
https://mathoverflow.net/questions/433949/consequences-resulting-from-yitang-zhangs-latest-claimed-results-on-landau-sieg
https://mp.weixin.qq.com/s/7cbydb_2vYSLzpiQ6Qb2lw
https://mp.weixin.qq.com/s/OgOsgp2wklSw86LQSnpuAA
https://www.zhihu.com/question/360965839/answer/2113995432
本文多处参考了知乎答主「gujurat」对该论文内容和意义的洞见和分析,在此表示感谢!
公众号后台回复“画图模板”获取90+深度学习画图模板~
![]()
备注:姓名-学校/公司-研究方向-城市(如:小极-北大-目标检测-深圳)
即可申请加入极市目标检测/图像分割/工业检测/人脸/医学影像/3D/SLAM/自动驾驶/超分辨率/姿态估计/ReID/GAN/图像增强/OCR/视频理解等技术交流群
极市&深大CV技术交流群已创建,欢迎深大校友加入,在群内自由交流学术心得,分享学术讯息,共建良好的技术交流氛围。