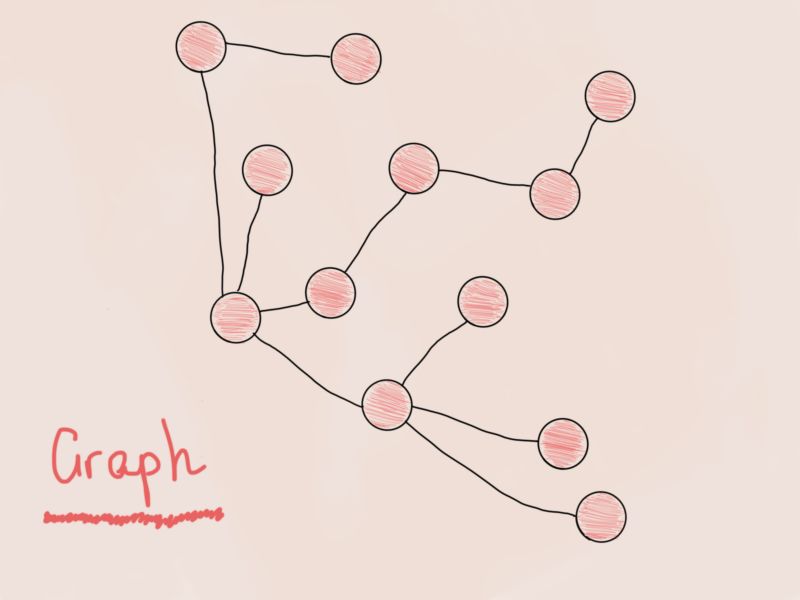
手把手:四色猜想、七桥问题…程序员眼里的图论,了解下?(附大量代码和手绘)
大数据文摘作品
编译:张礼俊、王一丁、xixi、修竹、Apricock、惊蛰、Chloe、龙牧雪
长文预警!本文作者Vardan Grigoryan是一名后端程序员,但他认为图论(应用数学的一个分支)的思维应该成为程序员必备。
本文从七桥问题引入,将会讲到图论在Airbnb房屋查询、推特推送更新时间、Netflix和亚马逊影片/商品个性化推荐、Uber寻找最短路线中的应用,附有大量手把手代码和手绘插图,值得收藏。
图论的傻瓜式教程
图论是计算机科学中最重要、最有趣,同时也是最容易被误解的领域之一。理解并使用图论有助于我们成为更好的程序员。图论思维应该成为我们的思维方式之一。
先看一下枯燥的定义……图是一组节点V和边E的集合,包括有序对G =(V,E)……🙄
在试图研究理论并实现一些算法的同时,我发现自己经常因为这些理论和算法太过艰深而被卡住......
事实上,理解某些东西的最好方法就是应用它。我们将展示图论的各种应用,及其详细的解释。
对于经验丰富的程序员来说,下面的描述可能看起来过于详细,但相信我,作为一个过来人,详细的解释总是优于简洁的定义的。
所以,如果你一直在寻找一个“图论的傻瓜式教程”,你看这篇文章就够了。
免责声明
免责声明1:我不是计算机科学/算法/数据结构(特别是图论方面)的专家。 我没有参与本文谈及的公司的任何项目。本文问题的解决办法并非完美,也有改进的空间。 如果你发现任何问题或不合理的地方,欢迎你发表评论。 如果你在上述某家公司工作或参与相应的软件项目,请提供实际解决方案。请大家耐心阅读,这是一篇很长的文章。
免责声明2:这篇文章在信息表述的风格上与其它文章有所不同,看起来可能图片也与其所在部分的主题不是十分契合,不过耐心的话,相信最终会发现自己对图片有完整的理解。
免责声明3:本文主要是将初级程序员作为受众而编写的。在考虑目标受众的同时,但更专业的人员也将通过阅读本文有所发现。
哥尼斯堡的七桥问题
让我们从经常在图论书中看到的“图论的起源”开始——哥尼斯堡七桥问题。
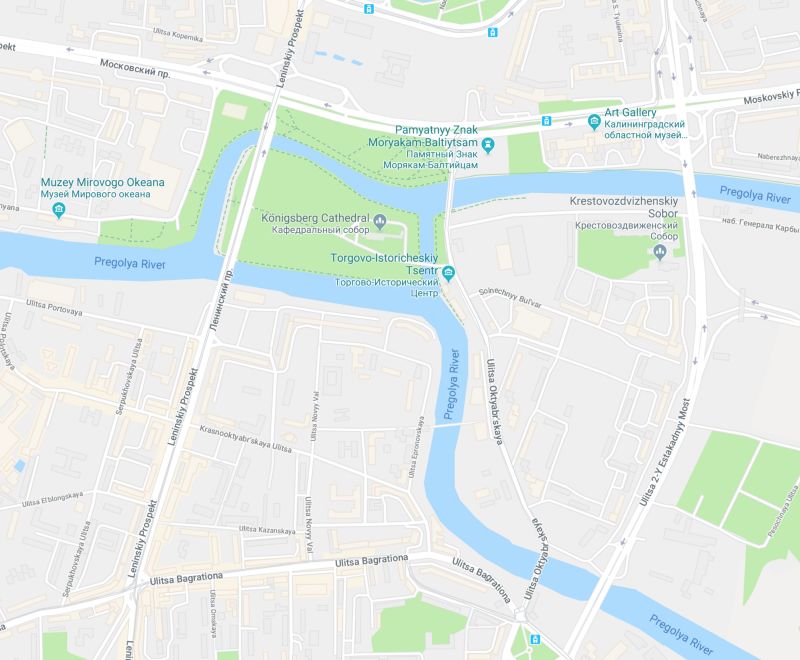
故事发生在东普鲁士的首都哥尼斯堡(今俄罗斯加里宁格勒),普莱格尔河(Pregolya)横贯其中。十八世纪在这条河上建有七座桥,将河中间的两个岛和河岸联结起来。
现在这个地区变成这样啦
问题是如何才能不重复,不遗漏地一次走完七座桥,最后回到出发点。他们当时没有互联网,所以就得找些问题来思考消磨时间。以下是18世纪哥尼斯堡七座桥梁的示意图。
你可以尝试一下,用每座桥只通过一次的方式来走遍整个城市。“每座桥”意味着不应该有没有通过的桥。“只有一次”意味着不得多次通过每座桥。如果你对这个问题很熟悉,你会知道无论怎么努力尝试这都是不可能的;再努力最终你还是会放弃。
Leonhard Euler(莱昂哈德·欧拉)
有时,暂时放弃是合理的。欧拉就是这样应对这个问题的。虽然放弃了正面解决问题,但是他选择了去证明“每座桥恰好走过并只走过一遍是不可能的”。让我们假装“像欧拉一样思考”,先来看看“不可能”。
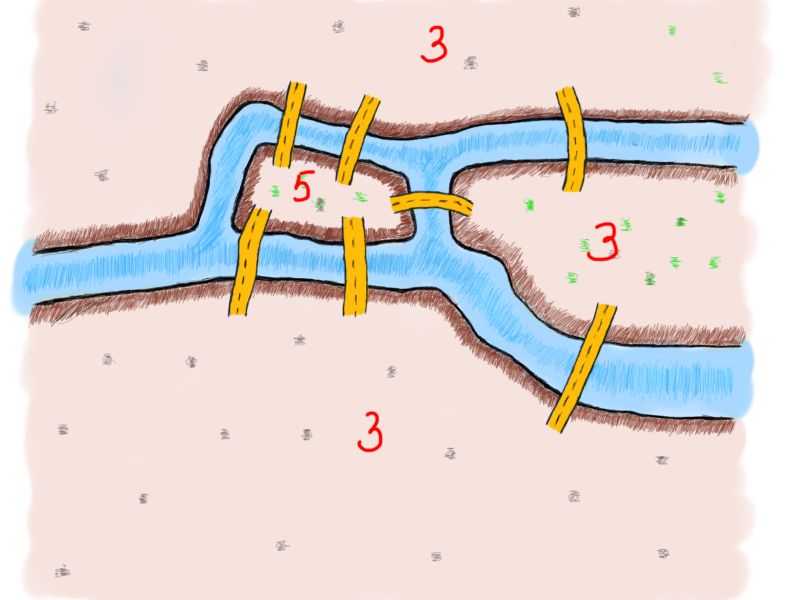
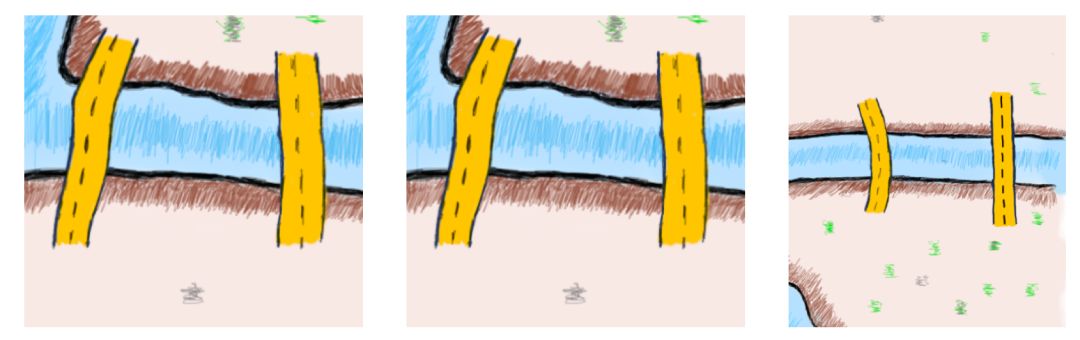
图中有四块区域——两个岛屿和两个河岸,还有七座桥梁。先来看看连接岛屿或河岸的桥梁数量中的模式(我们会使用“陆地”来泛指岛屿和河岸)。
每块区域连接桥梁的数量
只有奇数个的桥梁连接到每块陆地。这就麻烦了。
两座桥与陆地的例子
在上面的插图中很容易看到,如果你通过一座桥进入一片陆地,那你可以通过走第二座桥离开这片陆地。
每当出现第三座桥时,一旦穿过桥梁进入,那就没法走上每座桥且只走一次离开了。如果你试图将这种推理推广到一块陆地上,你可以证明,如果桥梁数量是偶数的话,总有办法离开这块陆地,但如果桥梁数量是奇数,就不能每桥走且只走一次的离开。试着记住这个结论。
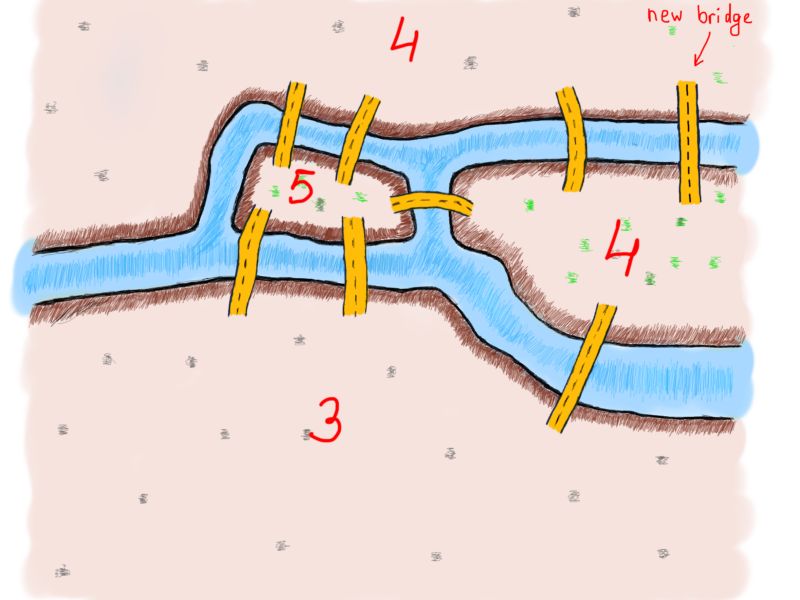
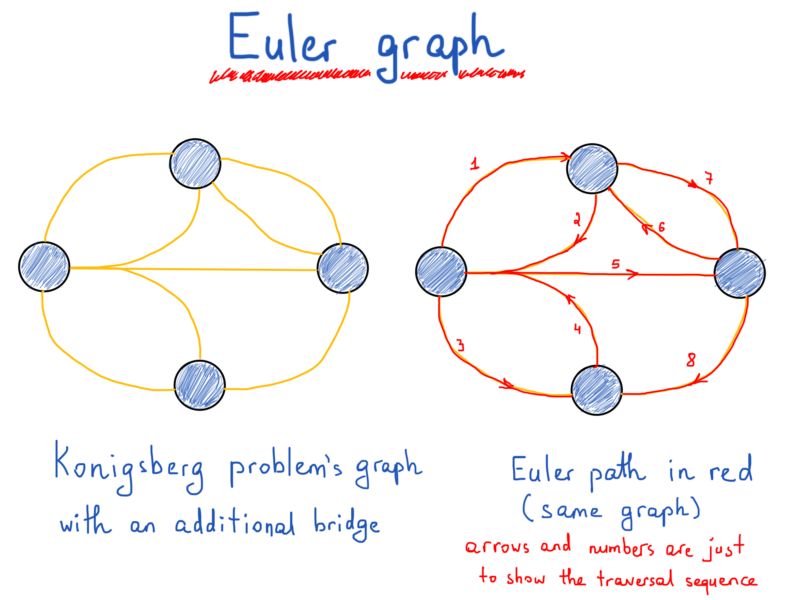
如果添加一个新的桥梁呢?通过下面这张图,我们可以观察各个陆地所连接的桥的数量变化及其影响。
注意新出现的桥
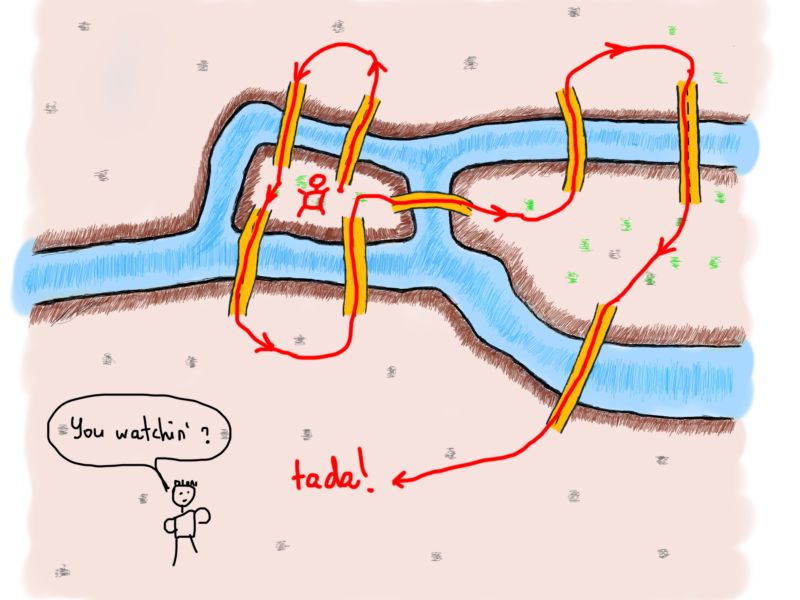
现在我们有两个偶数和两个奇数。让我们画一条包括了新桥梁的路线。
Wow
桥梁的数量是偶数还是奇数至关重要。现在的问题是:我们知道了桥梁数量是否就能够断定问题可不可解?为了解决问题桥的数量必须是偶数吗?欧拉找到了一种方法证明这个问题。而且,更有趣的是,具有奇数个桥梁连接的陆地数量也很重要。
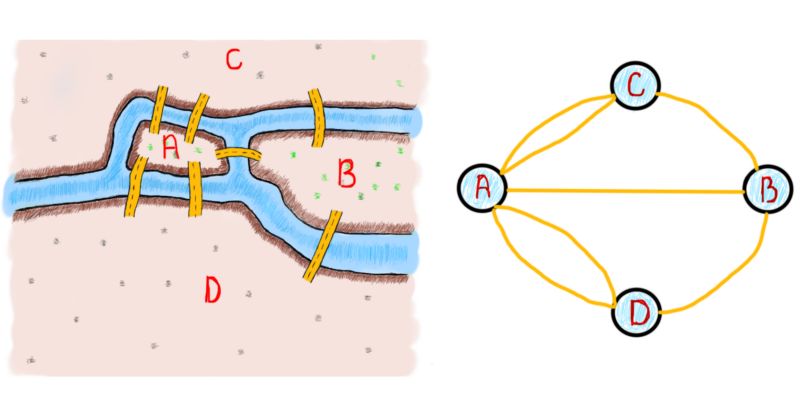
欧拉开始将陆地和桥梁“转换”成我们所知道的图。以下是代表哥尼斯堡七桥的图的样子(请注意,我们“暂时”增加的桥并不在图中):
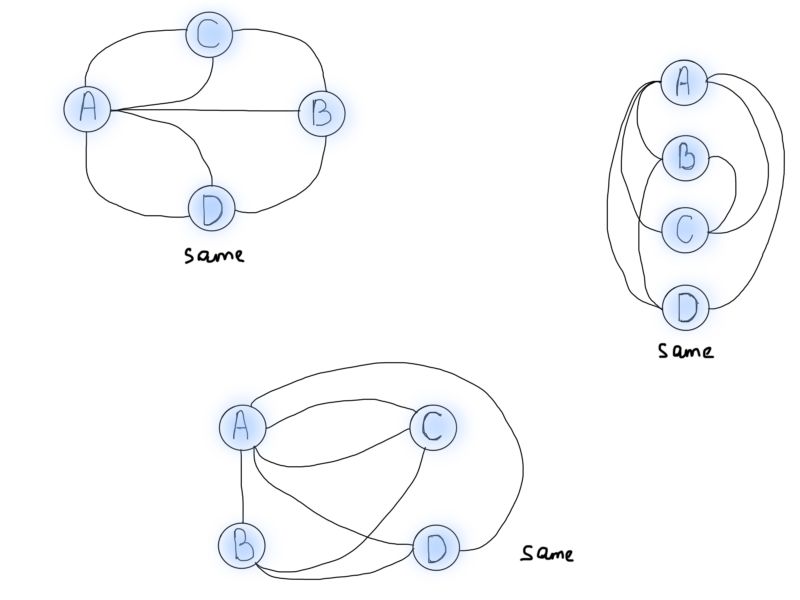
需要特别注意的一点是对问题的概括和抽象。无论何时你解决一个具体的问题,最重要的是归纳类似问题的解决方案。在这个例子中,欧拉的任务是归纳桥梁问题,以便能在未来推广到类似问题上,比如说世界上所有的桥梁问题。可视化还有助于以不同视角来看问题。下面的每张图都表示前面描述的桥梁问题:
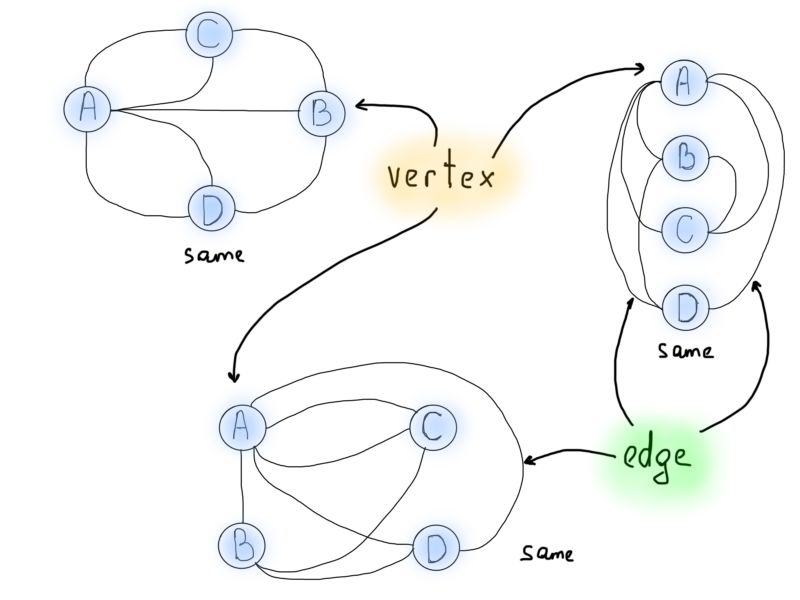
所以说图形化可以很好地描绘问题,但我们需要的是如何使用图来解决哥尼斯堡问题。观察从圆圈中出来的线的数量。从专业角度而言,我们将称之为“节点”(V),以及连接它们的“边”(E)。V代表节点(vertex),E代表边(edge)。
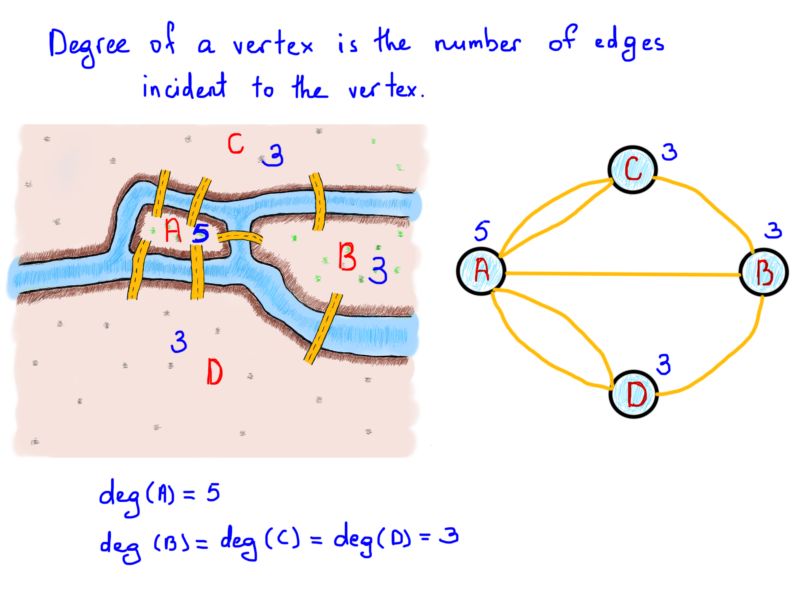
下一个重要的概念就是所谓的节点自由度,即入射(连接)到节点的边的数量。在上面的例子中,与陆地连结的桥的数目可以视为图的节点自由度。
欧拉证明了,一次并仅有一次穿过每条边(桥)来遍历图(陆地)严格依赖于节点(陆地)自由度。由这些边组成的路径叫做欧拉路径。欧拉路径的长度是边的数量。
有限无向图G(V,E)的欧拉路径是一条使G的每条边出现并且只出现一次的路径。如果G有一条欧拉路径,那么就可以称之为欧拉图。
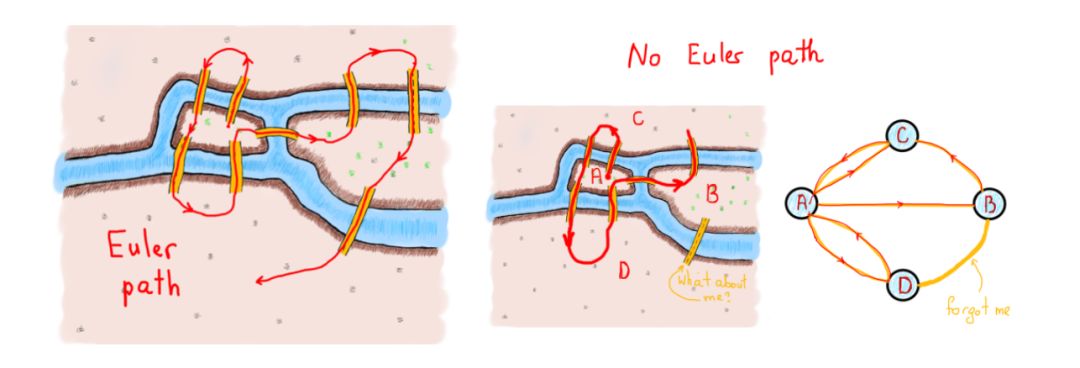
定理:一个有限无向连通图是一个欧拉图,当且仅当只有两个节点有奇数自由度或者所有节点都有偶数自由度。在后一种情况下,曲线图的每条欧拉路径都是一条闭环,前者则不是。
左图正好有两个节点具有奇数自由度,右图则是所有节点都是奇数自由度
首先,让我们澄清上述定义和定理中的新术语。
有限图是具有有限数量的边和节点的图。
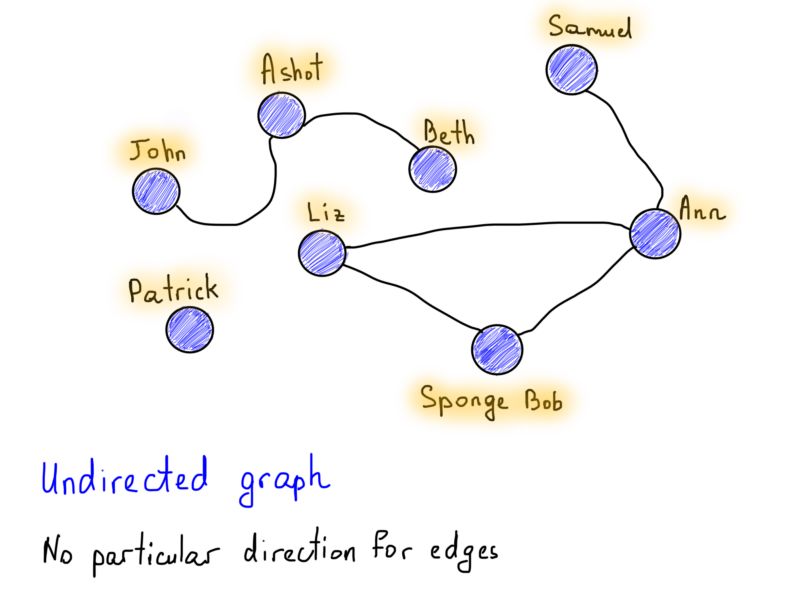
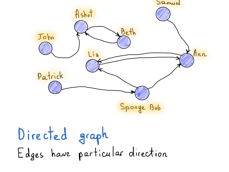
图可以是有向图也可以是无向图,这是图的有趣特性之一。举个非常流行的关于有向图和无向图的例子,Facebook vs. Twitter。Facebook的友谊关系可以很容易地表示为无向图,因为如果Alice是Bob的朋友,那么Bob也必须是Alice的朋友。 没有方向,都是彼此的朋友。
还要注意标记为“Patrick”的节点,它有点特别,因为没有任何连接的边。但“Patrick”点仍然是图的一部分,但在这种情况下,我们会说这个图是不连通的,它是非连通图(与“John”,“Ashot”和“Beth”相同,因为它们与图的其他部分分开)。在连通图中没有不可达的节点,每对节点之间必须有一条路径。
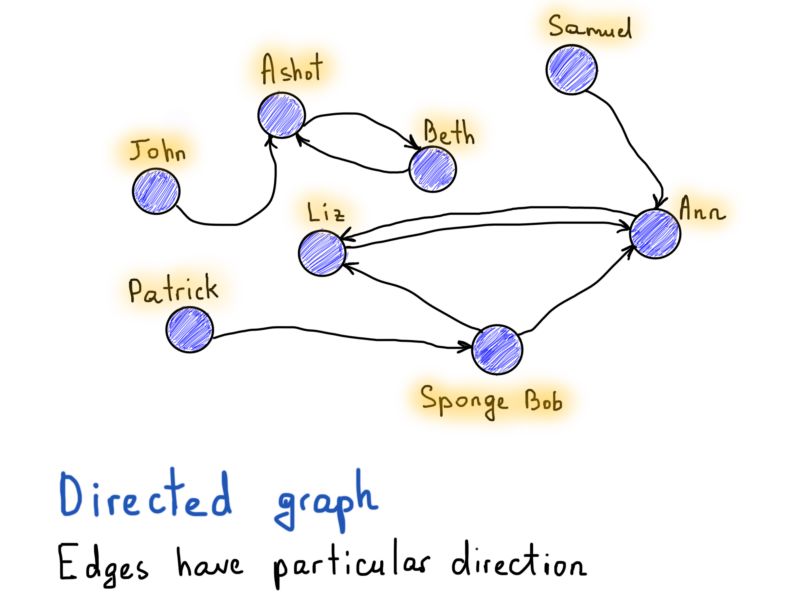
与Facebook的例子相对,如果Alice在Twitter上关注Bob,那不需要Bob回粉Alice。所以一个“关注”关系必须有一个方向来指示是谁关注谁,图表示中就是哪个节点(用户)有一个有向边(关注)到另一个节点。
现在,知道什么是有限连通无向图后,让我们回到欧拉图:
为什么我们首先讨论了哥尼斯堡桥问题和欧拉图呢?通过思考实际问题和上述解决方案,我们触及了图理论的基本概念(节点,边,有向,无向),避免了只有枯燥的理论。然而我们还未完全解决欧拉图和上述问题。我们现在应该转向图的计算机表示,因为这对我们程序员来说是最重要的。通过在计算机程序中表示图,我们能设计一个标记图路径的算法,从而确定它是否是欧拉路径。
图表示法:介绍
这是一项非常乏味的任务,要有耐心。记得数组和链表之间的竞争吗?如果你需要对元素进行快速访问,请使用数组;如果你需要对元素进行快速插入/删除等修改,请使用列表。
我不相信你会在“如何表示列表”的问题上有困惑。但是就图的表示而言,实际上却有很多麻烦,因为首先需要你决定的是用什么来表示一个图。相信我,你不会喜欢这个过程的。邻接表,邻接矩阵,还是边表?抛个硬币来决定?
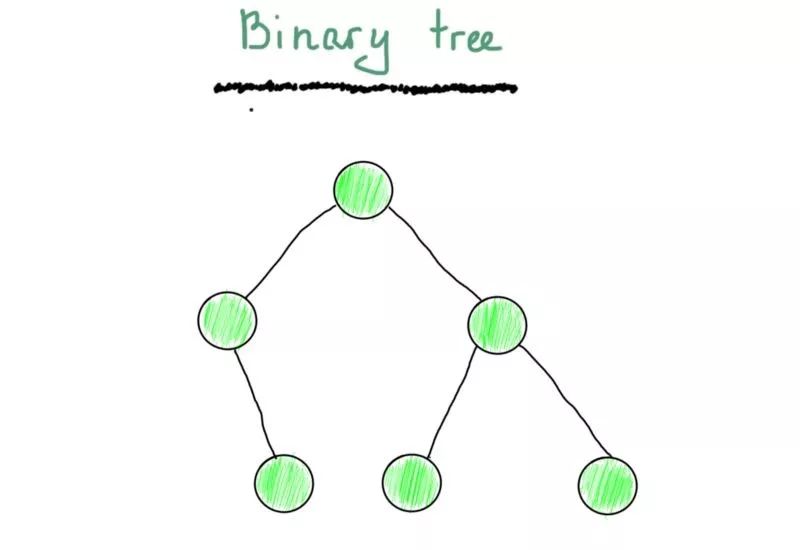
决定了用什么表示图了吗?我们将从一棵树开始。你应该至少看过一次二叉树(以下不是二叉搜索树)。
仅仅因为它由顶点和边组成,它就是一个图。你也许还记得最常见的一棵二叉树(至少在教科书中)的样子。
对于已经熟悉“树”的人来说,这段文字可能看起来太过细致了,但我还是要详细解释以确保我们的理解一致(请注意,我们仍在使用伪代码)。
BinTreeNode<Apple>* root = new BinTreeNode<Apple>("Green");
root->left = new BinTreeNode<Apple>("Yellow");
root->right = new BinTreeNode<Apple>("Yellow 2");
BinTreeNode<Apple>* yellow_2 = root->right;
yellow_2->left = new BinTreeNode<Apple>("Almost red");
yellow_2->right = new BinTreeNode<Apple>("Red");
如果你不熟悉树,请仔细阅读上面的伪代码,然后按照此插图中的步骤操作:
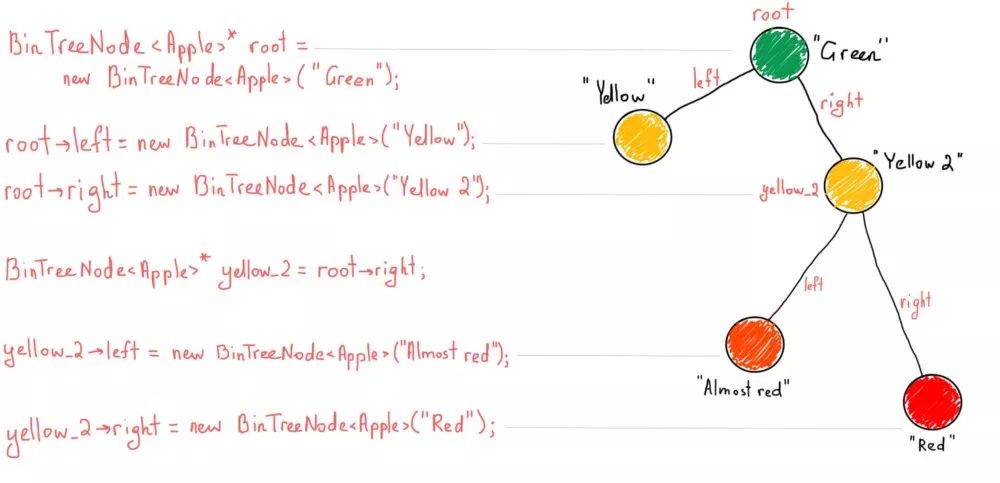
虽然二叉树是一个简单的节点“集合”,每个节点都有左右子节点,但二叉搜索树却由于应用了一个允许快速键查找的简单规则显得更加有用。
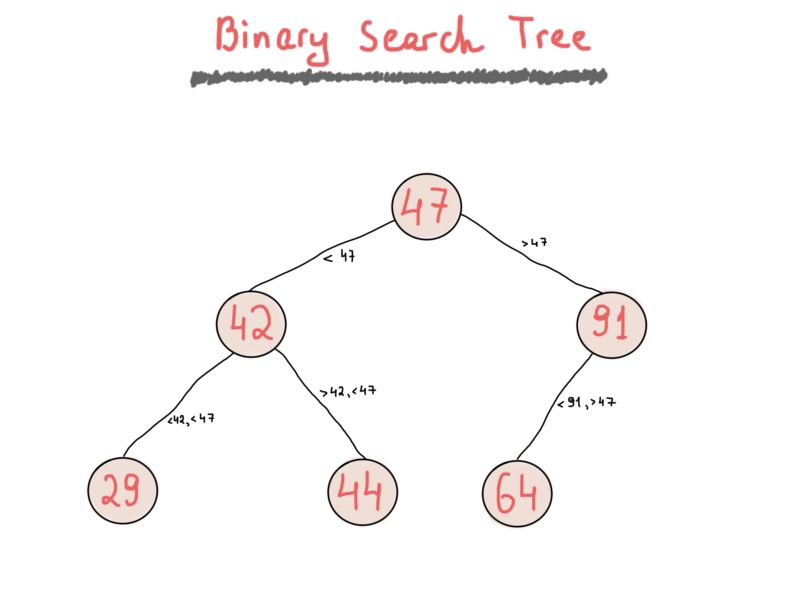
二叉搜索树(BST)对各节点排序。你可以自由地使用任何你想要的规则来实现你的二叉树(尽管可能根据规则改变它的名字,例如最小堆或最大堆),BST一般满足二分搜索属性(这也是二叉搜索树名字的来源),即“每个节点的值必须大于其左侧子树中的任何值,并且小于其右侧子树中的任何值”。
关于“大于”的阐述有个非常有趣的评论。这对于BST的性质也至关重要。当将“大于”更改为“大于或等于”,插入新节点后,BST可以保留重复的值,否则只将保留一个具有相同值的节点。你可以在网上找到关于二叉搜索树非常好的文章,我们不会提供二叉搜索树的完整实现,但为了保持一致性,我们还是会举例说明一个简单的二叉搜索树。
Airbnb房屋查询实例:二叉搜索树
树是一种非常实用的数据结构,你可能在项目开始的时候没有打算应用树这种结构,但是不经意间就用到了。让我们来看一个构想的但非常有价值的例子,关于为什么要首先使用二叉搜索树。
二叉搜索树中这个名字中包括了“搜索”,所以基本上所有需要快速查找的东西都应该放进二叉搜索树中。应该不代表必须,在编程中最重要的事情就是要牢记用合适的工具解决问题。在许多案例中用复杂度为O(N)的简单链表查找比复杂度为O(logN)的二叉搜索树查找更好。
通常我们会使用一个库实现BST,最常用的是C++里面的std::set或是std::map,然而在这个教程中,我们完全可以重新造轮子,重写一个BST库(BST几乎可以通过任何通用的编程语言库实现,你可以找到你喜欢的语言的相应文档)。
下面是我们将要解决的问题:
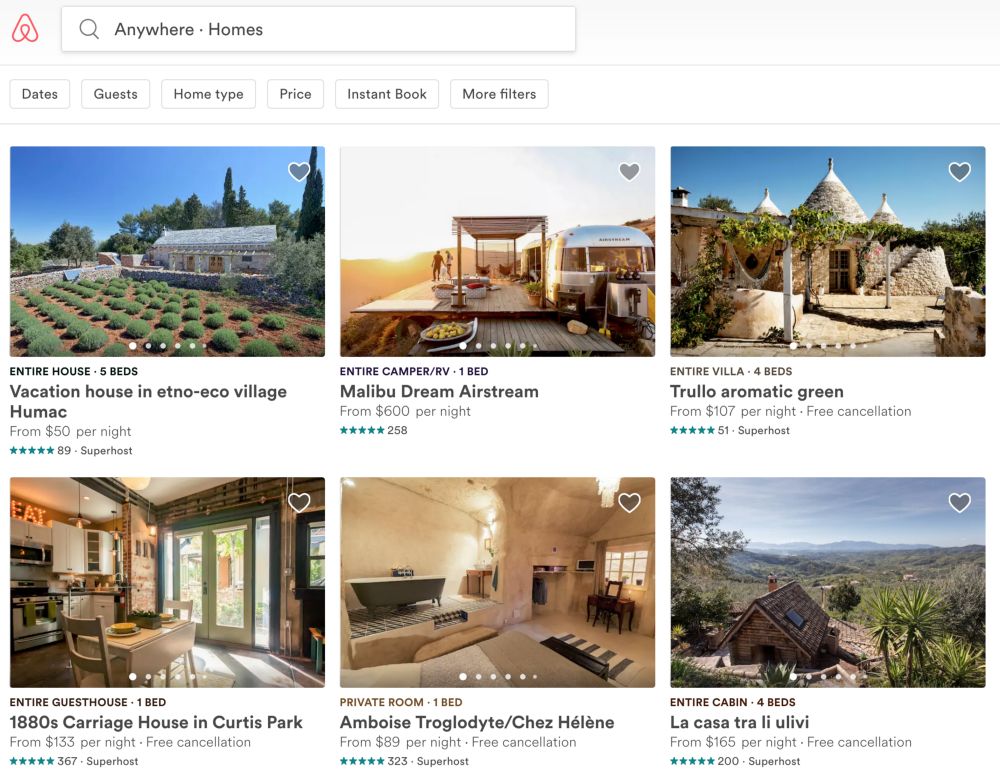
Airbnb房屋搜索截图
如何用一些过滤器尽可能快地根据一些查询语句搜索住房是一个困难的问题;当我们考虑到Airbnb储存了上百万的房源信息后这个问题会变得更困难。
所以当用户搜索住房时,他们有机会接触到数据库中大概四百万个房源记录。当然,网站主页上只能显示有限个排名靠前的住房列表,并且用户几乎不会好奇地去浏览住房列表里百万量级的住房信息。我没有任何关于Airbnb的分析,但是我们可以用一个在编程中叫做“假设”的强大工具,所以我们假设一个用户最多浏览一千套房源。
这里最重要的因素是实时用户数量,因为这会导致数据结构、数据库选择的不同和项目结构的不同。可以很明显的看出,如果只有100个用户,我们一点不必担心,但如果一个国家的实时用户数量远超过百万量级的阙值,我们必须要十分明智地做每一个决定。
是的,“每一个”决定都需要明智的决策。这就是为什么公司在服务方面力求卓越而雇佣最好的员工。Google, Facebook, Airbnb, Netflix, Amazon, Twitter还有许多其他的公司,他们需要处理大量的数据,做出正确的选择以通过每秒数以百万的数据来服务数以百万的实时用户,这一切从招聘好的工程师开始。这就是为什么我们程序员在面试中要与数据结构、算法和解决问题的逻辑作斗争,因为他们所需要工程师需要具有以最快最有效的方式解决大规模问题的能力。
现在案例是,一个用户访问Airbnb主页并且希望找到最合适的房源。我们如何解决这个问题?(注意这是一个后端问题,所以我们不需关心前端或者网络阻塞或者多个http链接一个http或者Amazon EC2链接主集群等等)。
首先,我们已经熟悉了一种强大的编程工具(是假设而不是抽象),让我们从假设我们所处理的数据都能放在内存中。你也可以假设我们的内存已经足够大。多大的内存是足够的呢?这是另外一个好问题。储存真实的数据需要多大的内存,如果我们正在处理四百万单位个数据(假设),而且我们或许知道每个单位的大小,那么我们就可以轻易的算出需要的内存大小,例如,4M*一个单位的大小。让我们来考虑一个“home”对象和他的特征,
事实上,让我们考虑至少一个在解决问题时需要处理的特征(一个“home”就是一个单位)。我们把它表示为C++语言结构的伪代码,你可以很轻松的将它转换成MongoDB架构或者其它你想要的形式,我们只是讨论特征名字和类型(想象为节约空间所使用的二元位域或位集)。
// feel free to reorganize this struct to avoid redundant space
// usage because of aligning factor
// Remark 1: some of the properties could be expressed as enums,
// bitset is chosen for as multi-value enum holder.
// Remark 2: for most of the count values the maximum is 16
// Remark 3: price value considered as integer,
// int considered as 4 byte.
// Remark 4: neighborhoods property omitted
// Remark 5: to avoid spatial queries, we're
// using only country code and city name, at this point won't consider
// the actual coordinates (latitude and longitude)
struct AirbnbHome
{
wstring name; // wide string
uint price;
uchar rating;
uint rating_count;
vector<string> photos; // list of photo URLs
string host_id;
uchar adults_number;
uchar children_number; // max is 5
uchar infants_number; // max is 5
bitset<3> home_type;
uchar beds_number;
uchar bedrooms_number;
uchar bathrooms_number;
bitset<21> accessibility;
bool superhost;
bitset<20> amenities;
bitset<6> facilities;
bitset<34> property_types;
bitset<32> host_languages;
bitset<3> house_rules;
ushort country_code;
string city;
};
假设,上面的结构显然不是完美的,还有许多假设和未完成的部分(免责声明里我也说了)。我只是观察Airbnb的过滤器和设计属性列表来满足查找需求。这只是一个例子。现在我们要计算每个AirbnbHome对象需要占用多少内存。
名字只是一个支持多种语言标题的wstring,这意味着每个字符会占用2字节(如果我们用其它语言可能不需要考虑字符大小,但是在C++中,char占用1字节,wchar占用2字节)。
对于Airbnb住房列表的快速浏览让我们假设住房的名字最多包含100个字符(大多数都在50个字符左右,而不是100),所以我们将假设最大值为100,这就意味着占用不超过200字节的内存。uint是4字节,uchar为1字节,ushort为2字节(这些都是假设)。
假设图片用第三方存储服务储存,比如Amazon S3(目前为止,我知道这个假设对于Airbnb来说很可能是真实的,但是这只是一个假设),另外我们有这些照片的链接,考虑到链接没有标准的大小限制,但通常都不会超过2083个字符,所以我们用这个当作链接的最大大小。因为每个房源平均会有5张照片,所以图片最多占用10KB内存。
让我们重新考虑,通常存储服务提供的链接有一部分是固定的。
例如http(s)://s3.amazonaws.com/<bucket>/<object>,这是构建链接时常见的规律,所以我们只需要储存真实图片的ID。让我们假设我们用一种ID生成器来对图片产生20字节长的不重复的ID字符串。
那么每张图片的链接就会是这样: https://s3.amazonaws.com/some-know-bucket/<unique-photo-id>
这让我们节省了空间,储存五张图片的ID只需要100字节的内存。同样的小技巧也可以应用在房东的ID上面,例如房东的ID需要20字节的内存(事实上我们对用户只用了整数ID,但是考虑到一些数据库系统有自己专用的ID生成器,如MongoDB,我们假设20字节长度的ID只是一个中位数,使它可以几乎满足所有数据库系统的变化。Mongo产生的ID大小为24字节)。
最后,我们用4个字节表示长度为32的位集,对于长度大于32小于64的位集用8个字节表示。注意这里的假设,我们在这个例子中用位集表示任意一个数值特征,但是它也可以取多个值,用另一种方法来说,就是一种多项选择的复选框。
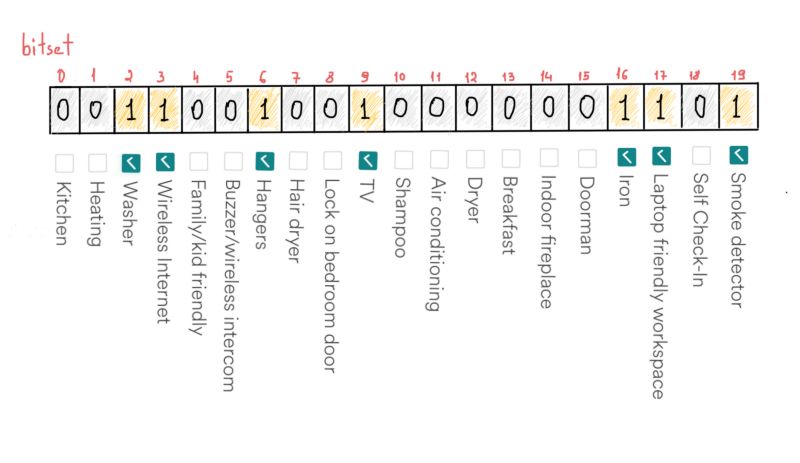
例如,每个Airbnb房源都有一个关于可用设施的列表,比如熨斗、洗衣机、电视、wifi、衣架、烟雾报警、甚至笔记本办公区域等。或许房子里有超过20种设施,但我们依然把这个数目固定为20,因为这个数目是Airbnb过滤页面中可选择的设备数量。
如果我们用合理的顺序排列设备的名字,位集可以帮助我们节省一些空间。比如说,如果一个房子里有上述提到的设备(在截图中打勾的设备),我们可以在位集里对应的位置填充一个1。
位集能够用20个比特存储20个不同值
例如,检查房间里是否有“洗衣机”:
bool HasWasher(AirbnbHome* h)
{
return h->amenities[2];
}
或者更专业的:
const int KITCHEN = 0;
const int HEATING = 1;
const int WASHER = 2;
//...
bool HasWasher(AirbnbHome* h)
{
return (h != nullptr) && h->amenities[WASHER];
}
bool HasWasherAndKitchen(AirbnbHome* h)
{
return (h != nullptr) && h->amenities[WASHER] && h->amenities[KITCHEN];
}
bool HasAllAmenities(AirbnbHome* h, const std::vector<int>& amenities)
{
bool has = (h != nullptr);
for (const auto a : amenities) {
has &= h->amenities[a];
}
return has;
}
你可以尽可能地改善代码(并且改正编写的错误),我们只是想强调在这个问题背景下使用位集的思想。
同样也适用于“房屋守则”、“住房类型”等。正如上面代码的注释中提到的,我们不会储存经纬度以避免地理位置上的查询,我们会储存国家代码和城市名字来缩小地址的查找范围(删除掉街道只是为了简化)。
国家代码可以用2或3个字符或3个数字表示,我们会用数字化的表示并且用ushort表示每个国家代码。
城市往往比国家多,所以我们不能用“城市代码”(尽管我们可以生成一些作为内部使用),我们直接使用真实的城市名称,为每个名字平均预留50字节的内存,对于特殊的城市名比如Taumatawhakatangihangakoauauotamateaturipukakapikimaungahoronukupokaiwhenuakitanatahu (85 个字母),我们最好用另外的布尔变量来表示这个是一个特殊的非常长的城市名字(不要试图读出这个名字)。
所以,记住字符串和向量的内存消耗,我们将添加额外的32字节确保最后结构的大小不会超出。我们还会假设我们在64位的系统上工作,尽管我们为int和short选择了最合适的值。
// Note the comments
struct AirbnbHome
{
wstring name; // 200 bytes
uint price; // 4 bytes
uchar rating; // 1 byte
uint rating_count; // 4 bytes
vector<string> photos; // 100 bytes
string host_id; // 20 bytes
uchar adults_number; // 1 byte
uchar children_number; // 1 byte
uchar infants_number; // 1 byte
bitset<3> home_type; // 4 bytes
uchar beds_number; // 1 byte
uchar bedrooms_number; // 1 byte
uchar bathrooms_number; // 1 byte
bitset<21> accessibility; // 4 bytes
bool superhost; // 1 byte
bitset<20> amenities; // 4 bytes
bitset<6> facilities; // 4 bytes
bitset<34> property_types; // 8 bytes
bitset<32> host_languages; // 4 bytes, correct me if I'm wrong
bitset<3> house_rules; // 4 bytes
ushort country_code; // 2 bytes
string city; // 50 bytes
};
420字节加上之前提到的额外32字节,总共452字节的容量,考虑到有时候你或许会受困于一些校准因素,所以让我们把容量调到500字节。那么每条房屋信息占用500字节内存,对于包含所有房屋信息的列表(有时候我们会混淆列表数量和真实房屋数量,如果我犯错了请告诉我),占用内存约500字节*4百万=1.86GB,近似2GB,这个结果看起来很合理。
我们在创建结构的时候做了许多假设,努力节约内存来缩小成本,我估计会最后地结果会超过2GB,如果我在计算中出错,请告诉我。接下来,无论我们要怎么处理这些数据,我们都需要至少2GB的内存。请克服你无聊的感觉,我们才刚要开始。
现在是这项任务中最难的部分。针对这个问题选择正确的数据结构(最高效的列表过滤方法)不是最难的部分。(对我来说)最难的是用大量的过滤器查找这些列表。
如果只有一个查找关键词(只有一个过滤器)那么问题会更容易解决。假设用户只对价格感兴趣,那么我们需要做的就只是选择在这个价格范围内的Airbnb房源。下面是我们用二叉搜索树完成这项任务的例子。
想象全部四百万的房屋对象,这棵树会变得十分巨大。当然,内存也会增长很多,因为我们用BST储存这些数据时,每个树上的节点都有另外两个指针指向它的左子节点和右子节点,这样每个子节点指针都会占用另外8字节(假设是64位的系统)。
对于四百万个节点来说,这些指针总共又会占用62MB,尽管这跟2GB原有的数据大小相比不算什么,但是我们也不能轻易忽视它们。
上个例子中树的所有节点都可以用O(logN)复杂度的算法找到。如果你不熟悉算法复杂度,不能侃侃而谈,我接下来会解释清楚,或者你可以直接跳过复杂度这部分。
算法复杂度
大多数情况下,计算一个算法的大O复杂度是比较容易的。提醒一下,我们总是只关心最坏的情况,也就是算法获得正确结果(解决问题)所需要的最大操作次数。
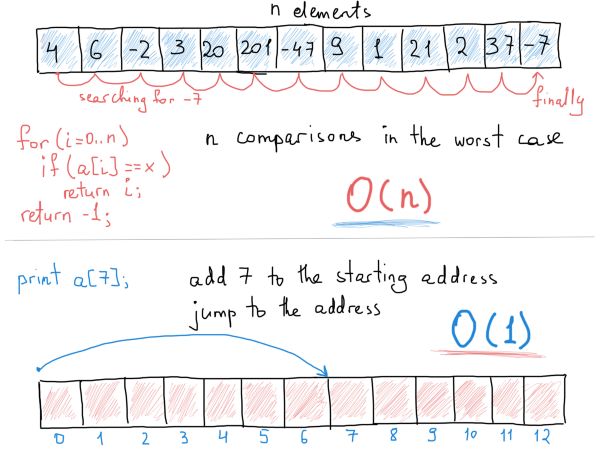
假设有一个包含100个元素的无序数组,需要比较多少次我们才能找到任意指定元素(同时也考虑指定元素缺失的情况)?
我们需要将每个元素值和我们要找的值相比较,即使这个要找的元素有可能在数组的第一位(只需要一次比较),但是我们只考虑最坏的情况(要么元素缺失,要么是在数组的最后一位),所以答案是100次。
“计算”算法复杂度其实就是在操作数和输入大小之间找到一个依赖关系,上面那个例子中数组有100个元素,操作数也是100次,如果数组元素个数(输入)增加到1423个,找到任意指定元素的操作数也增加到1423次(最坏的情况下)。
所以在这个例子中,输入大小和操作数的关系是很明显的线性关系:数组输入增加多少,操作数就增加多少。
复杂度的关键所在就是找到这个随输入数增加操作数怎么变化的规律,我们说在无序数组中查找某一元素需要的时间为O(N),旨在强调查找它的过程会占用N次操作(或者说占用N次操作*某个常数值,比如3N)。
另一方面,在数组中访问某个元素只需要常数时间,即O(1)。这是因为数组结构是一个连续数据结构,持有相同类型的元素(别介意 JS数组),所以“跳转”到特定元素只需要计算其到数组第一个元素间的相对位置。
我们非常清楚二叉搜索树将其节点按序排列。那么在二叉搜索树中查找一个元素的算法复杂度是多少呢?
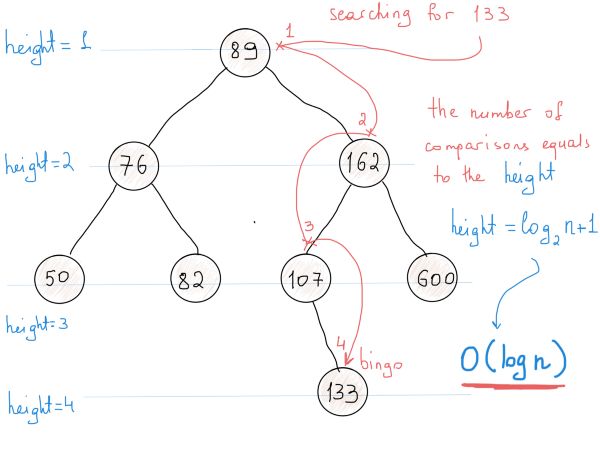
此时我们应该计算找到指定元素(在最坏情况下)所需要的操作数。看插图,从根部开始搜索,第一次比较行为将导致三种结果,(1)发现节点,(2)若指定元素值小于节点值,则继续与节点左子树比较,或(3)指定元素值大于节点值,则与右子树比较。
在每一步中我们都可以把所需考虑的节点减少一半。在BST中查找元素所需要的操作数(也就是比较次数)与树的高度一致。
树高是最长路径上的节点数。在这个例子中树高为4。如图所示,高度计算公式为:以2为底logN+1。所以搜索的复杂度为O(logN+1) = O(logN)。所以最坏情况下,在400万个节点中搜索需要log4000000=~22次比较。
再说回树。二叉搜索树中元素访问时间为O(logN)。为什么不用哈希表呢?哈希表具有常数访问时间,因此几乎任何地方都可以用哈希表。
在这个问题中我们必须要考虑一个很重要的条件,那就是我们必须能够进行范围搜索,例如搜索从房价80美元到162美元的区间内的房子。
在BST中只需要对树进行一次中序遍历并保留一个计数器就可以很容易可以得到一个范围内的所有节点。而相同任务对于哈希表有点费时了,所以对于特定的例子来说选择BST还是很合理的。
不过还有另外一个地方让我们重新考虑使用哈希表。
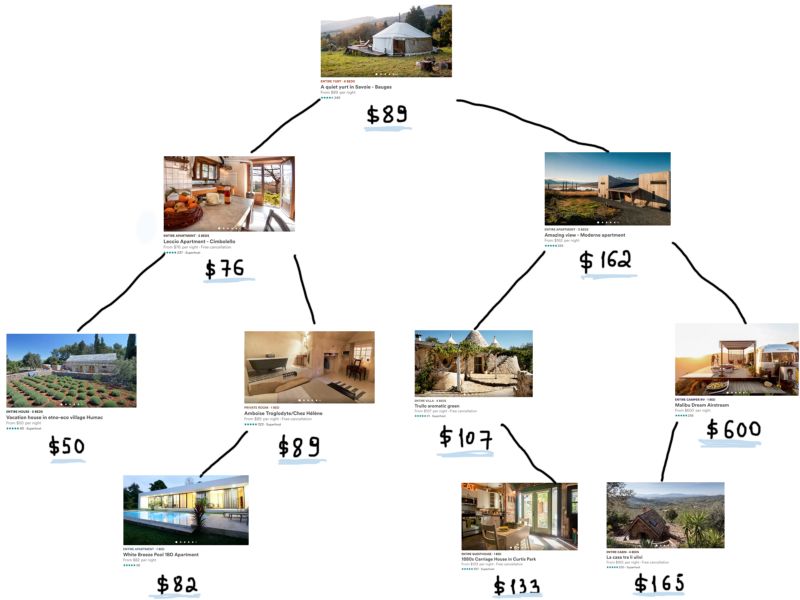
那就是价格分布。价格不可能一直上涨,大部分房子处在相同的价格区间。看上面这个截图,直方图向我们展示了价格的真实情况,数以百万计的房价在同一个区间(18美元到212美元),他们平均价格是相同的。
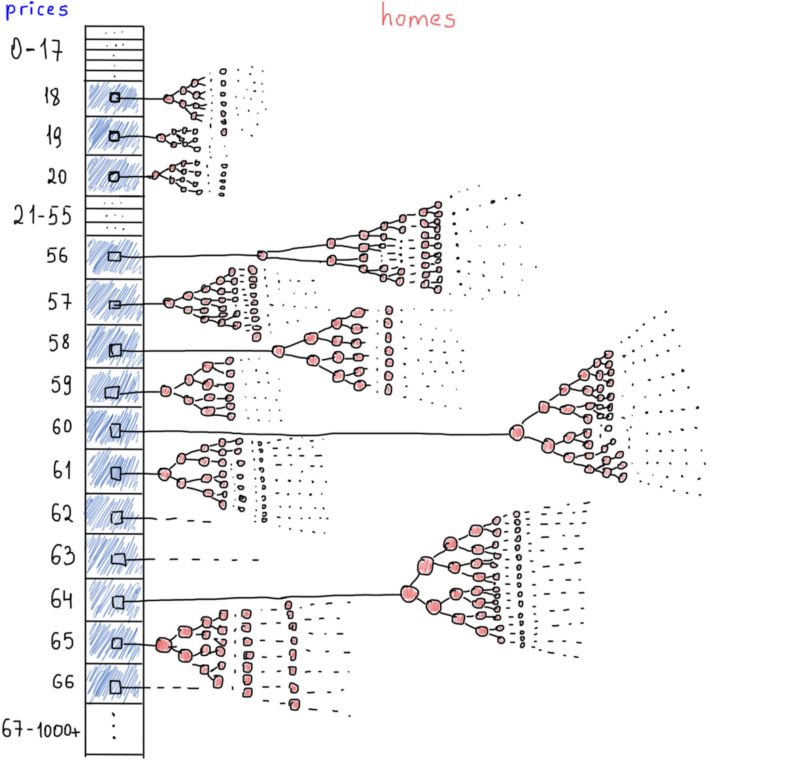
简单的数组也许能起到很好的作用。假设一个数组的索引是价格,房子列表按照价格排序,我们可以在常量时间内获得任意价格区间(额,几乎是常数)。下面是它的样子(抽象来讲):
就像哈希表,我们可以按照价格访问每一组房屋。价格相同的所有房屋都归在同一个单独的BST下。而且如果我们存储的是房屋的ID而不是上面定义的整个对象(AirbnbHome结构),会节省下一些空间。最有可能的情况是,将所有房屋的完整对象保存在一个哈希表中,房屋ID映射房屋对象,同时建立另一个哈希表(或者一个数组),用房屋ID映射价格。
当用户请求一个价格区间时,我们从价格表中获取房屋ID,将结果分割成固定大小(也就是分页,通常一个页面上显示10-30个条目),通过房屋ID获取完整房屋信息。记住这些方法。
同时,要记住平衡。平衡对BST来讲至关重要,因为这是在O(logN)内完成操作的唯一保证。不平衡BST的问题很明显,当你在排序中插入元素时,树最终会变成一个链表,这显然会导致具有线性时间性质的操作次数。
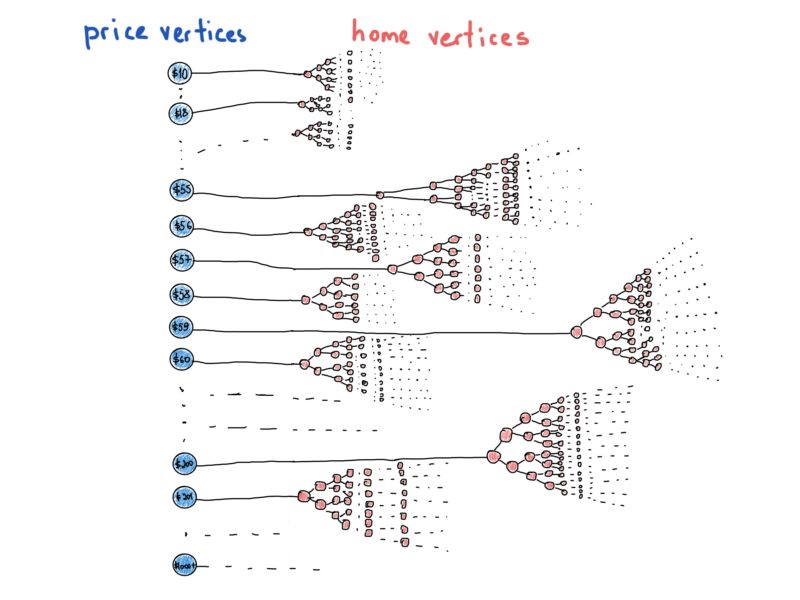
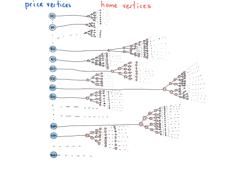
不过从现在开始可以忘记这些,假设我们所有的树都是完全平衡的。再看一眼上面的插图,每个数组元素代表一颗树。那如果我们把插图改成这样:
这更像一个“真实”的图了。这个插图描绘了了最会伪装成其他数据结构的数据结构——图。
图表示法:进阶
关于图有一个坏消息,那就是对于图表示法并没有一个固定的定义。这就是为什么你在库里找不到std::graph的原因。不过BST其实可以代表一个“特殊”的图。关键是要记住,树是图,但图并不仅仅是树。
上个插图表示在单个抽象条件下可以有许多树,图中包含“价格vs房屋”和具有“不同”类型的节点,价格是只具有价格数值的图节点,并指向满足指定价格的所有住房ID(住房节点)的树。它很像一个混合的数据结构,而不是我们在课本例子中常常见到的简单的一个图。
这就是图表示法的关键,它并没有固定的和“合法的”结构用于图表示(不像BST有指定的基于节点的表示法,有左/右子指针,尽管你也可以用一个数组来表示一个BST)。
只要你“认为”它是一个图,你可以用你觉得最方便的方式(对特定问题最便捷)表达它。“认为是一个图”所表达的就是应用特定于图的算法。
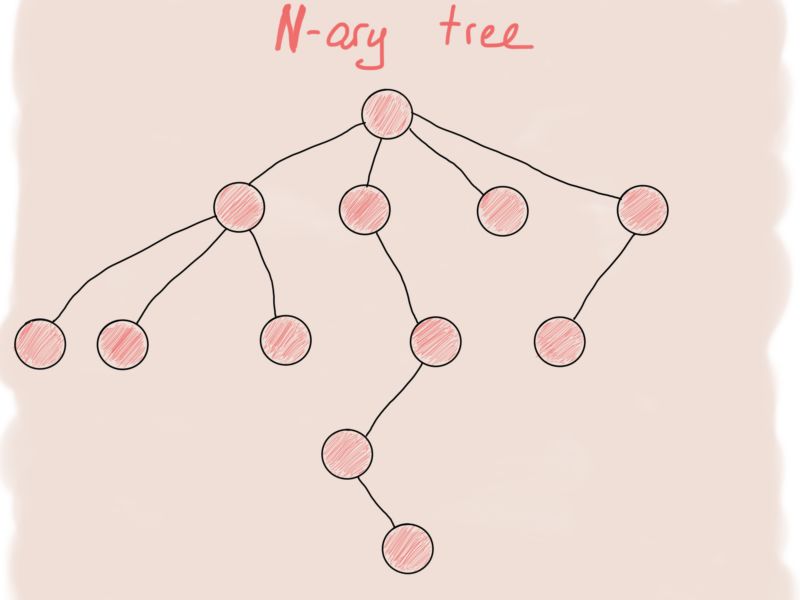
其实N叉树更像一个图。
首先想到来表示N叉树节点的伪代码是这样的:
struct NTreeNode
{
T value;
vector<NTreeNode*> children;
};
这个结构只表示这个树的一个节点,整棵树应该是这样的:
// almost pseudocode
class NTree
{
public:
void Insert(const T&);
void Remove(const T&);
// lines of omitted code
private:
NTreeNode* root_;
};
这个类模拟一个名为root_树节点。我们可以用它构建任意大小的树。这是树的起始点。为了增加一个新的树节点我们需要分配给它一个内存并将该节点添加到树的根节点上。
图与N叉树虽然很像,但稍微有点不同。试着画出来一下。
这个是图吗?说不是也是。它跟之前的N叉树是一样的,只是旋转了一下。根据经验来讲,不管何时你看到一棵树,也不管这是一颗苹果树,柠檬树还是二叉搜索树,你都可以确定他也是一个图。所以为图节点(图顶点)设计一个结构,我们可以得出相同的结构:
struct GraphNode
{
T value;
vector<GraphNode*> adjacent_nodes;
};
这足以构成一个图吗?当然不能。看看之前的两个图有什么不同。
都是图
左边插图中的图中的树没有一个“输入”点(更像是一个森林而不是单独的树),相反的是右侧插图中的图没有不可到达的顶点。听起来很熟悉哈。
定义:如果每对节点间都有一条路径,那么我们认为这个图是连通的。
很明显,在“价格vs房屋”图中并不是每对节点间都有路径(如果从插图中看不出来,就假设价格节点并没有彼此相连吧)。尽管这只是一个例子来解释我们不能构造一个具有单个GraphNode struct的图,但有些情况下我们必须处理像这样的非连通图。看看这个类:
class ConnectedGraph
{
public:
// API
private:
GraphNode* root_;
就像N叉树是围绕一个节点(根节点)构建的,一个连通图也是围绕一个根节点构造的。树是“有根”的,也就是说存在一个起始点。连通图可以表示成一个有根树(和几个属性),这已经很明显了,但是要记住即使对于一个连通图,实际表示会因算法不同而异,因问题不同而异。然而考虑到图的基于节点的性质,非连通图可以表示为:
class DisconnectedGraphOrJustAGraph
{
public:
// API
private:
std::vector<GraphNode*> all_roots_;
};
对于像DFS/BFS这样的图遍历,很自然就使用树状表示了。这种表示方法帮助很大。然而,像有效路径跟踪这样的例子就需要不同的表示了。还记得欧拉图吗?
为了找到一个图具有“欧拉性”,我们应该在其中找到一个欧拉路径。这意味着通过遍历每条边一次去访问所有的节点,并且如果遍历结束还有未走过的边,那就说明这个图没有欧拉路径,因此也就不是欧拉图。
还有一个更快些的方法,我们可以检查所有节点的自由度(假设每个节点都存有它的自由度),然后根据定义,如果图有个数不等于两个的奇自由度节点,那这个图就不是欧拉图。
这个检查行为的复杂度是O(|V|),|V|是图中节点的个数。当插入新的边来增加奇/偶自由度时我们可以进行追踪,这个行为复杂度为O(1)。这是非常快速。不过不用在意,我们只要画一个图就行了,仅此而已。下面的代码表示一个图和返回路径的Trace()函数。
// A representation of a graph with both vertex and edge tables
// Vertex table is a hashtable of edges (mapped by label)
// Edge table is a structure with 4 fields
// VELO = Vertex Edge Label Only (e.g. no vertex payloads)
class ConnectedVELOGraph {
public:
struct Edge {
Edge(const std::string& f, const std::string& t)
: from(f)
, to(t)
, used(false)
, next(nullptr)
{}
std::string ToString() {
return (from + " - " + to + " [used:" + (used ? "true" : "false") + "]");
}
std::string from;
std::string to;
bool used;
Edge* next;
};
ConnectedVELOGraph() {}
~ConnectedVELOGraph() {
vertices_.clear();
for (std::size_t ix = 0; ix < edges_.size(); ++ix) {
delete edges_[ix];
}
}
public:
void InsertEdge(const std::string& from, const std::string& to) {
Edge* e = new Edge(from, to);
InsertVertexEdge_(from, e);
InsertVertexEdge_(to, e);
edges_.push_back(e);
}
public:
void Print() {
for (auto elem : edges_) {
std::cout << elem->ToString() << std::endl;
}
}
std::vector<std::string> Trace(const std::string& v) {
std::vector<std::string> path;
Edge* e = vertices_[v];
while (e != nullptr) {
if (e->used) {
e = e->next;
} else {
e->used = true;
path.push_back(e->from + ":-:" + e->to);
e = vertices_[e->to];
}
}
return path;
}
private:
void InsertVertexEdge_(const std::string& label, Edge* e) {
if (vertices_.count(label) == 0) {
vertices_[label] = e;
} else {
vertices_[label]->next = e;
}
}
private:
std::unordered_map<std::string, Edge*> vertices_;
std::vector<Edge*> edges_;
};
注意这些无处不在的bug。上面的代码包含大量的假设,比如打标签,因此我们知道顶点有一个字符串类型的标签。你可以随意将它换成任何你想要的东西,不必太在意这个例子里的内容。然后还有命名,代码注释中写道,VELOGraph是Vertex Edge Label Only Graph的缩写(我起的名字)。
重点是,这个图表示法包含一个表,用来将节点标签和节点连接的边映射到该顶点,还包含一个边的列表,该列表含有节点对(由特定边连接)和仅由Trace()函数使用的标记(flag)。
回顾Trace()函数实现过程,边的标记(flag)用来表示已经遍历过的边(在任何Trace()被调用后都需要重置标记)。
推特时间线实例:多线程推送
邻接矩阵是另一种非常有用的有向图的表示方法,推特的关注情况图即是一个有向图。
有向图
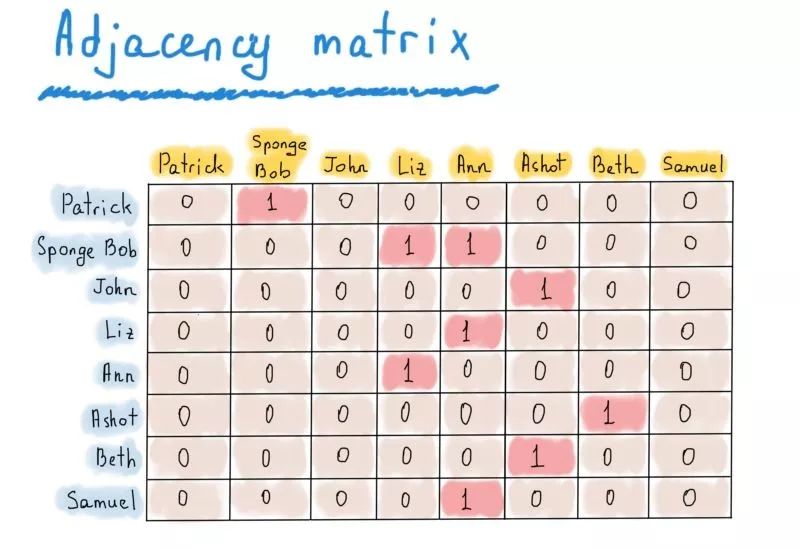
这个推特的示例图中,共有8个节点。因此我们只需将这个图表示为|V|×|V|的方阵(|V|行|V|列,|V|为节点数)。如果节点v到u存在有向边,则矩阵的[v][u]元素为真(1),否则为假(0)。
推特的示例
可以看出,这个矩阵有些过于稀疏,但却有利于快速访问。想要知道Patrick是否关注了Sponge Bob,只需访问matrix["Patrick"]["Sponge Bob"];想要知道Ann的关注者都有哪些,只需运行出“Ann”的列(列头标黄);想要知道Sponge Bob关注了谁,只需运行出“Sponge Bob”的行。
邻接矩阵也可用于无向图,与有向图不同的是,若有一条边将v和u相连,则矩阵的[v][u]元素和[u][v]元素都应为1。无向图的邻接矩阵是对称的。
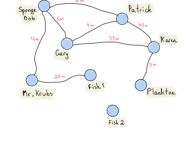
应注意到,邻接矩阵除了可以储存0和1,也可以储存“更有用”的东西,比如边的权重。表示地点之间距离的图就是一个再恰当不过的例子。
上图表示出了Patrick, Sponge Bob和其他人住址之间的距离(这也被称作加权图)。如果两个顶点之间没有直接路径,矩阵对应元素就置无穷符号“∞”。
这一阶段的无穷符号并不意味着二者之间一定不存在路径,也不意味着一定存在。元素的值可能在用算法找出顶点之间路径长度以后重新定义(若要更好地储存顶点和与之相连的边的信息,可利用关联矩阵)。
虽然邻接矩阵看起来很适合用于表示推特的关注情况图,但存储将近3亿用户(月活跃用户数)的布尔值需要300 * 300 * 1 字节,这是大约82000Tb(百万兆字节),也就是1024 * 82000Gb。
不知道你的磁盘有多少簇,但我的笔记本可没有这么大的内存。如果用位集呢?位棋盘有一点用,可以让所需存储空间缩减到10000Tb左右,但这还是太大了。前面提到过,邻接矩阵过于稀疏,因此想要储存全部有效信息,需要很多额外空间,因此表示与顶点相连的边的邻接表是更佳选择。
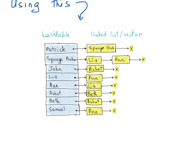
所谓更佳,是因为邻接矩阵既储存了“已关注”信息,也储存了“未关注”信息,而我们只需要知道关注情况,如下所示:
邻接矩阵 vs 邻接表
右侧的插图表示一个邻接表。每个表体现了图中一个顶点所有相邻顶点的集合。要指出的是,一个图可以用不同的邻接表来表示(荒谬但事实如此)。插图中标黄处使用了哈希表,这是一种相当明智的方法,因为哈希表查询顶点的时间复杂度是O(1)。
我们没有提到邻接顶点列表应该用哪一种特定的数据结构存储,链表、向量等都行,任你选择。关键在于,要想知道Patrick有没有关注Liz,我们需要访问哈希表(需要常数时间),遍历这个链表中的所有元素,并与“Liz”元素进行比较(需要线性时间)。
这种情况下,线性时间并不太坏,因为我们只需循环与“Patrick”相邻的顶点,而这些顶点的个数是一定的。那考虑到空间复杂度,这种表示方法是否还适用于推特的例子呢?我们需要至少3亿个哈希表来记录,每个都指向一个向量(我选择向量来避免列表左/右指针的内存消耗),每个向量里包含了...多少元素呢?
没有相关数据,只找到了推特关注数的平均值,707。假设每个哈希表指向707个用户id(每个占8字节),并假设哈希表每个表头只含有关键字(仍然是用户id),则每个哈希表占据3亿 * 8字节,哈希表关键字占据707 * 8字节,总共就是3亿 * 8 * 707 * 8字节,大约为12Tb。这个结果不算令人满意,但和一万多Tb相比已经好很多了。
说实在的,我不知道这个结果是否合理,但考虑到我在32Gb的专用服务器上花费约为30美元,那么分片储存12Tb需要至少385个这样的服务和400多台控制服务器(用于数据分发控制),因此每月需要大约1.2万美元。考虑到数据有副本,而且总会有些问题出现,我们将服务器的数量扩大到三倍,再增加一些控制服务器。
假设至少需要1500台服务器,则每月需要大约4.5万美元。我当然觉得这不可行,毕竟租用一台服务器于我都有些吃力,但对于Twitter则似乎算不上事(与真正的Twitter服务器相比,确实不算事)。
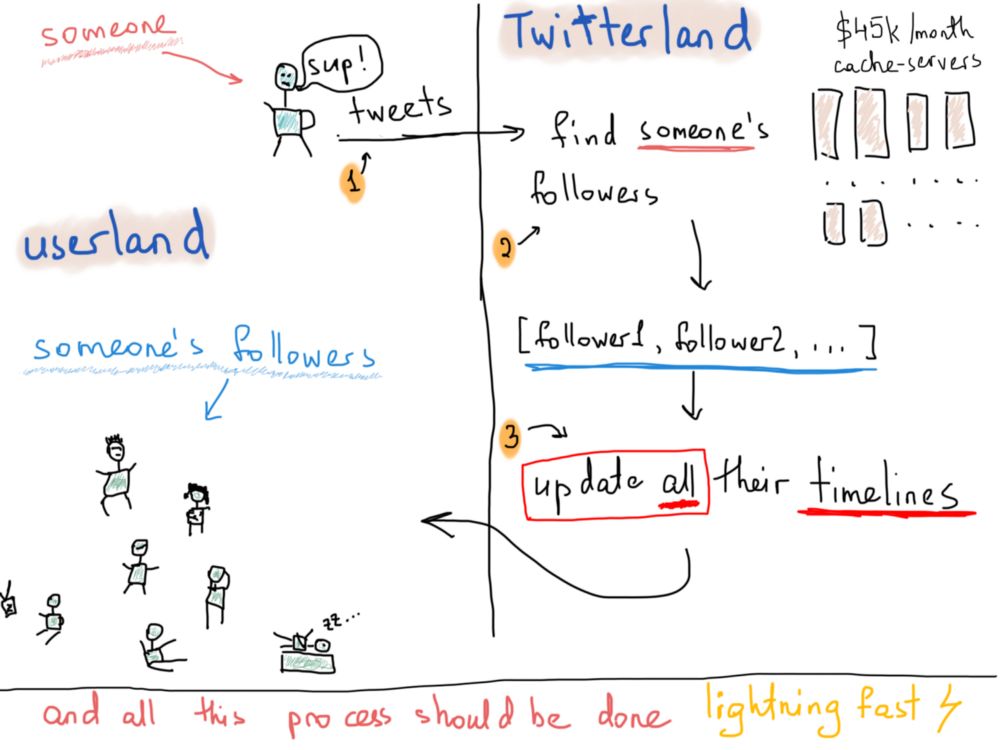
这样计算够了吗?并不是,我们只考虑了关注情况的数据。推特最重要的是什么?我是指,从技术上来说,最大的问题是什么?是能够快速将某人的一条推文推送给其关注者。而且不仅是快速,更像是闪电一样的光速。
假设Patrick发了一条关于食物想法的推文,他的所有关注者都应在一个合理的时间内收到这条推文。多长时间合理呢?我们当然可以随意假设,但我们感兴趣的是真实的系统。下图说明了有人发送推文的后续过程。
我们不知道一条推特需要多久才能推送给所有关注者,但公开的统计数据显示,每天有5亿条推文,因此上图的过程每天要重复5亿次。关于传达速度我找不到有用的数据,但可以模糊地回忆出,大约5秒之内,所有关注者都可以接收到推文。
而且还要考虑处理量很大的情况,比如有着上百万关注量的名人。他们可能只是在海滨别墅里用推文分享了美妙的早餐,推特却要辛辛苦苦把这“相当有用”的信息推送给以百万计的关注者。
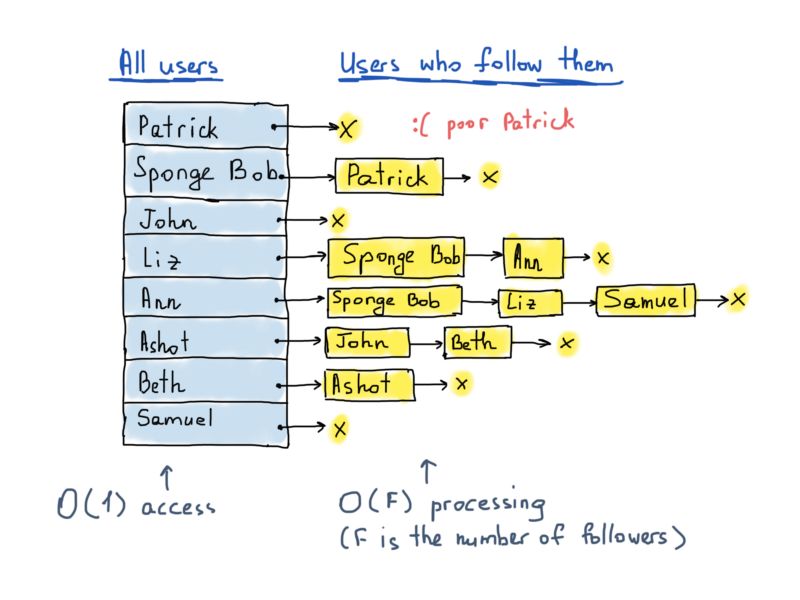
为了解决推文推送的问题,我们不需要关注情况的图,而需要关注者的图。关注情况图(用一个哈希表和一些列表表示)可以很方便的找出被某一个用户所关注的所有用户,但却不能找到某一个用户的所有关注者,要想达到这个目标需要遍历哈希表所有的关键字。
因此我们应当构造另一个图,这个图在某种程度上对称相反于前者。这个新的图应该也由3亿个顶点组成,每个顶点指向邻接顶点的列表(数据结构不变),不过这个列表代表关注者。
在上图所示的情况下,每当Liz发送推文,Sponge Bob和Ann都会在他们的时间线上看到更新。实现这一点有一个常用技术,即为每位用户的时间线保留一个单独的结构。在推特这个有3亿用户的例子里,我们大概假设需要至少3亿个时间线(每位用户一个)。
总的来说,当一个用户发送推文,我们应当获取该用户的关注者列表,并更新这些关注者的时间线(将内容相同的推文插入它们的时间线)。时间线可以用列表或是平衡树表示(以推文发送时间的数据作为节点)。
// 'author' represents the User object, at this point we are interested only in author.id
//
// 'tw' is a Tweet object, at this point we are interested only in 'tw.id'
void DeliverATweet(User* author, Tweet* tw)
{
// we assume that 'tw' object is already stored in a database
// 1. Get the list of user's followers (author of the tweet)
vector<User*> user_followers = GetUserFollowers(author->id);
// 2. insert tweet into each timeline
for (auto follower : user_followers) {
InsertTweetIntoUserTimeline(follower->id, tw->id);
}
}
这段代码只是我们从时间线真实的形式中提取出的思想,用多线程的方法可以加快推送的速度。
这种方法对于处理量很大的情况至关重要,因为对于上百万关注者来说,相较于处在关注者列表前端的用户,处于尾端的用户总是较晚看到新推文。下面一段伪代码尝试说明了多线程推送的想法:
// Warning: a bunch of pseudocode ahead
void RangeInsertIntoTimelines(vector<long> user_ids, long tweet_id)
{
for (auto id : user_ids) {
InsertIntoUserTimeline(id, tweet_id);
}
}
void DeliverATweet(User* author, Tweet* tw)
{
// we assume that 'tw' object is already stored in a database
// 1. Get the list of user's (tweet author's) followers's ids
vector<long> user_followers = GetUserFollowers(author->id);
// 2. Insert tweet into each timeline in parallel
const int CHUNK_SIZE = 4000; // saw this somewhere
for (each CHUNK_SIZE elements in user_followers) {
Thread t = ThreadPool.GetAvailableThread(); // somehow
t.Run(RangeInsertIntoTimelines, current_chunk, tw->id);
}
}
如此一来,无论关注者何时刷新时间线,总能接收到新推文。
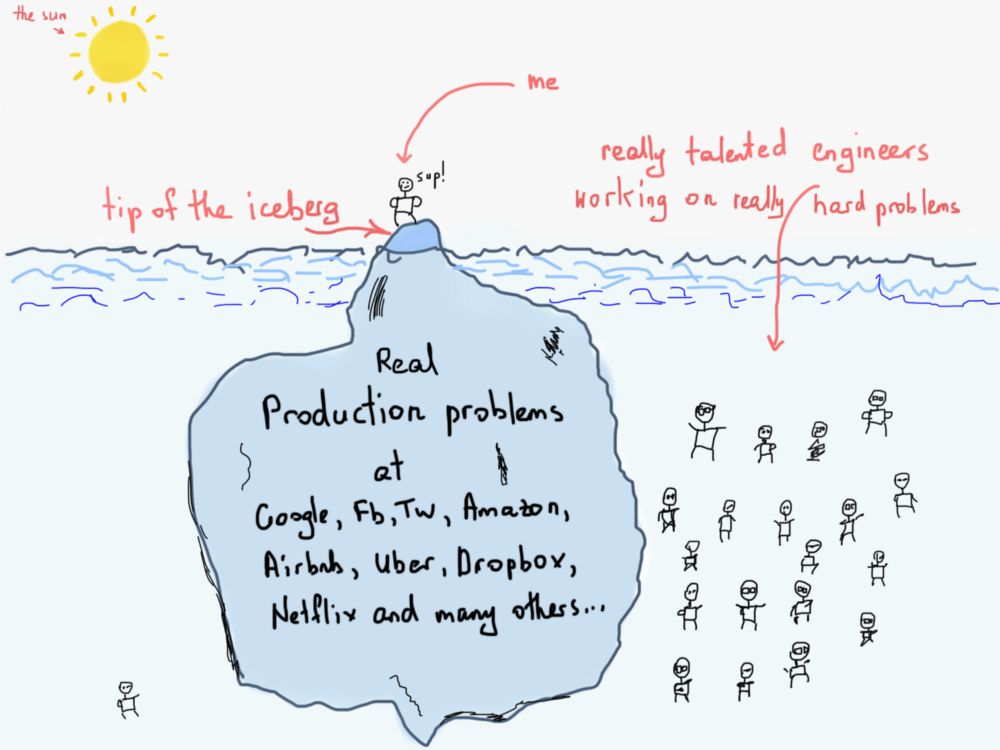
公道地说,我们不过才触及Airbnb或推特所面临问题的冰山一角。天才工程师们要耗费大量时间,才能构造出推特、谷歌、脸书、亚马逊、airbnb等了不起的复杂系统。阅读本文时别忘了这一点。
推特的例子的重点在于图的使用,尽管没有用到图算法,而只涉及到图的表示。我们的确用伪代码写了一个推送推文的函数,但这只是寻找解决方案过程的产物,我指的“图算法”是这个列表中的算法。
令程序员心力交瘁的图论和图算法应用,某种意义上来说是有些许差异的。前面我们讨论了不用图表示时,高效筛选Airbnb房源的问题。此时,一处明显的缺陷在于,若有两个或以上的筛选关键词,则无法高效筛选。可以图算法可以解决这个问题吗?这我不敢保证,不过可以试一试。
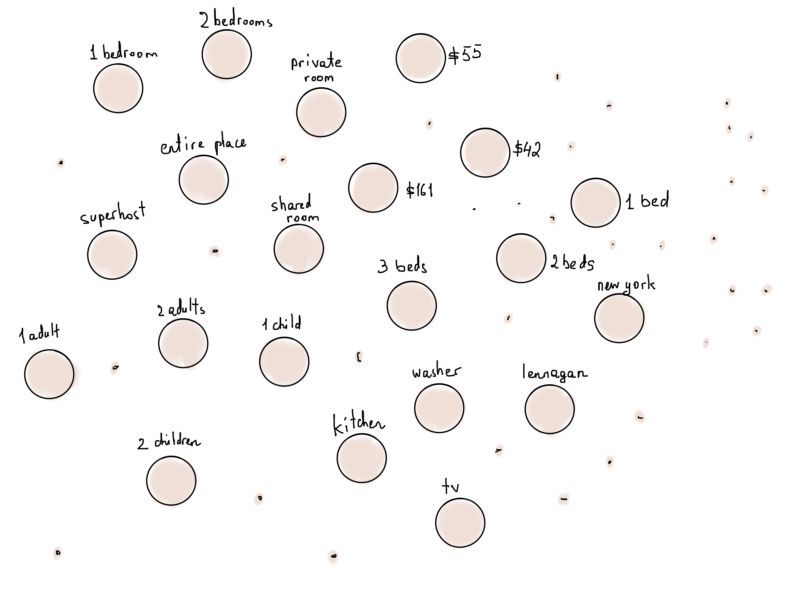
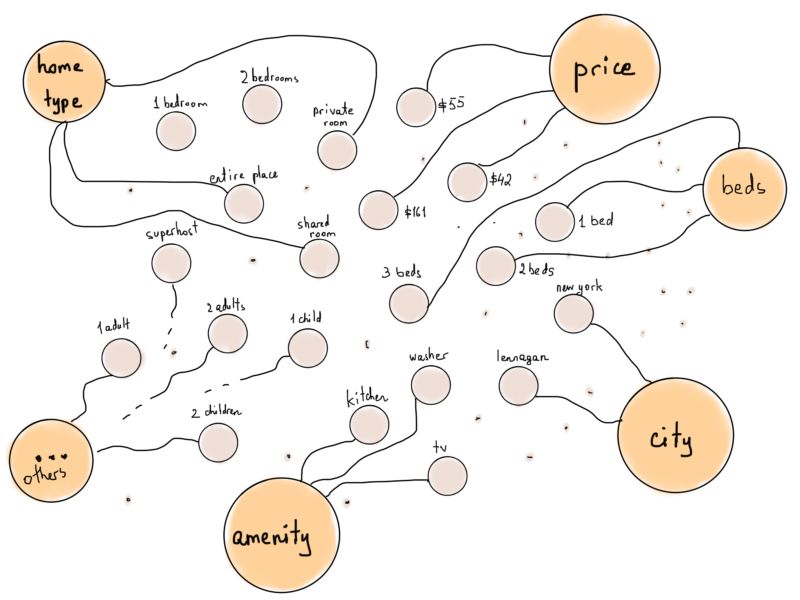
把每个筛选条件当作独立的顶点会有什么结果呢?字面地理解“每个筛选条件”,10美元到1000美元以上的价格、所有城市的名称、国家代码、生活设施(电视、Wi-Fi等等)、成人房客数等等,每个信息都作为一个独立的顶点。
将“类型”顶点加入图能使这些顶点更“好用”,比如将所有代表生活设施筛选条件的顶点连接到“生活设施”顶点。
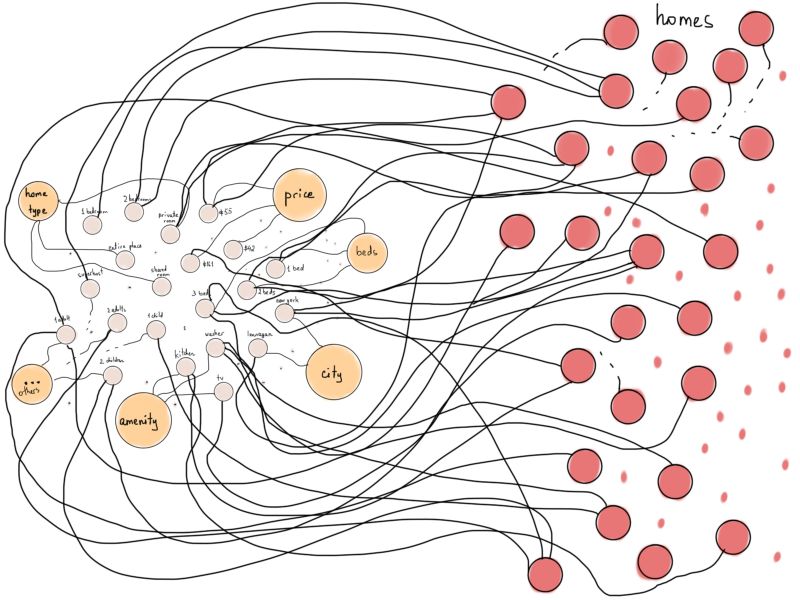
如果我们将Airbnb房源表示为顶点,并将它们连接到各自符合的筛选条件所对应的顶点上,会是什么情况呢(例如,若“房源1”有“厨房”这项设施,则将其连接至“厨房”)?
稍微处理一下这个示意图,能使之更像一种特殊的图:二分图。
顶点数量比图上显示的更多
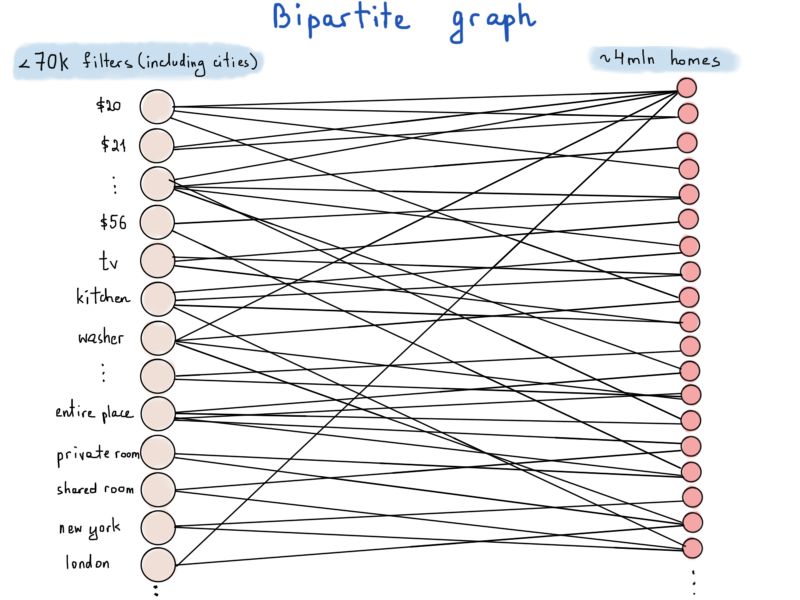
二分图(亦称偶图)是一种特殊的图,其顶点可分为两个不相交且独立的集合,从而每条边的两个顶点分别在两个集合中。在我们的例子中,一个集合代表筛选条件(以F表示),另一个代表房源(H)。
例如,有10万个房源标价为62美元,则有10万条边以“62美元”为一个顶点,每条边的另一顶点为满足该条件的房源。考虑空间复杂度最坏的情况,即每个房源满足所有的筛选条件,边总数应为7万 * 400万。
如果每条边用{筛选条件;房源}来表示,并用4字节的整型变量表示筛选条件、8字节的长整型变量表示房源,则每条边占据12字节。存储7万 * 400万个12字节的值大约需要3Tb的内存。
不过我们的计算中有一个小错误,由Airbnb的统计数据得知,7万个左右的筛选条件中约有6.5万个是房源所在城市。值得庆幸的是,一个房源不能位于两个或以上的城市。
这意味着与城市相连的边的总数实际应为400万(每个房源只位于一座城市),因此只用计算70000-65000=5000个筛选条件,故而只需5千 * 400万 * 12字节的内存,总计小于0.3Tb。
这个结果还不错。不过是什么构造出了这样的二分图呢?一般而言,网页/移动端请求会包括几个不同的筛选条件,例如这样:
house_type: "entire_place",adults_number: 2,price_range_start: 56,price_range_end: 80,beds_number: 2,amenities: ["tv", "wifi", "laptop friendly workspace"],facilities: ["gym"]
我们只需找到上述请求对应的所有“筛选条件顶点”,再运行得到所有和这些顶点相连的“房源顶点”,而这就将我们引向图算法。
图算法:介绍
任何针对图形的处理都可以被称作“图算法”。 你甚至可以以写个打印一个图里所有节点的函数,就叫做“我的节点打印算法”。大多数人觉得很难的是那些写在教科书上的算法。霍普克洛夫特-卡普算法(Hopcroft-Karp)就是个二分图匹配算法的例子。下面我们就来试着用这个算法来过滤Airbnb房源吧。
给定一个Airbnb房屋(H)和过滤器(F)的二分图,其中H的每个元素(顶点)都可以有多个相邻的F元素(顶点)相连。 请查找一个和F子集内顶点相邻的H顶点子集。
这个问题的描述已经很绕了,而我们现在甚至还不能确定Hopcroft-Karp算法是否能解决这个的问题。不过我向你保证,解决问题的这个过程会让我们学到很多在图算法背后的基本原理。不过,这个过程并不那么短,所以请大家耐心。
Hopcroft-Karp算法是种以一个二分图作为输入,并产生一个最大基数匹配(maximum cardinality matching)的算法。 最大基数匹配得出的结果是一组由尽可能多的边组成的集合,而集合中所有的边都不会共享节点。
熟悉这种算法的读者可能已经意识到,这并不能解决我们的Airbnb问题,因为匹配要求所有的边都不会共享节点。
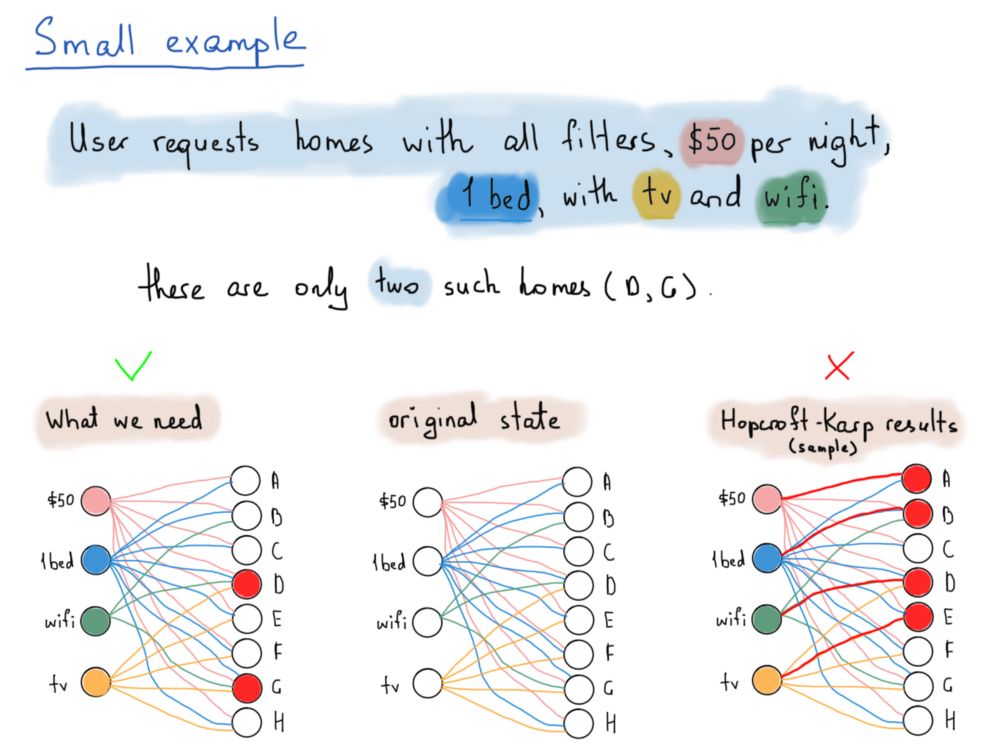
我们来看一个例子。为了简单起见,我们假设一共只有4个过滤器和8个房源。房源由A到H的字母表示,过滤器是随机选择的。假设四个过滤器分别为:每晚50美元,有一张床,提供Wifi,提供电视。
已知家庭A价格为50美元,有1张床。从A到H的所有房屋每晚价格都为50美元,床位为1张,但其中很少有提供WiFi或者电视的。下面这张插图详细说明了系统应返回哪一个房源,满足了顾客需求,即一间同时符合所有四种过滤器的住房。
这个问题的解决方案(见上图中左下角连线)要求能通过这些共享顶点的边找到那些可以通过所有四种过滤器的房屋(即D和G),而Hopcroft-Karp算法去掉了具有共同节点的边,最后得到的是入射到两个子集顶点的边(见上图中右下角的红线)。
就像上图中所展示的,在所有的选择中我们只需要同时满足所有条件的D和G就可以。我们真正需要找的,是共享节点的所有的边。
我们可以给这样的方法设计一种算法,但处理时间对于要求立刻回复的用户来说并不理想。相比之下,建立一个节点带有多个排序键值(key)的平衡二叉搜索树(balanced binary search tree)可能会更快。这有点像数据库的索引文件,直接把主键(primary keys)或者外键(foreign keys)映射到一组所需要的数据记录。
Hopcroft-Karp算法(以及其他许多算法)都是同时基于DFS(深度优先搜索)和BFS(广度优先搜索)图遍历算法。
实际上,在这里介绍Hopcroft-Karp算法的实际原因是可以从二叉树这样性质优良的图循序渐进地转入更难的图遍历问题。
二叉树遍历非常优美,主要是因为它们的递归性质。 二叉树有三种基本遍历,分别是先序,后序和中序遍历(你当然可以自己编写遍历算法)。
如果你曾经遍历过链表,那么遍历很容易理解。 在链表中只需打印当前节点的值(下面代码中的命名项)并在下一个节点继续这个操作即可。
// struct ListNode {
// ListNode* next;
// T item;
// };
void TraverseRecursive(ListNode* node) // starting node, most commonly the list 'head'
{
if (!node) return; // stop
std::cout << node->item;
TraverseRecursive(node->next); // recursive call
}
void TraverseIterative(ListNode* node)
{
while (node) {
std::cout << node->item;
node = node->next;
}
}
二叉树和这个差不多。首先打印这个节点的值(或其他任何需要使用的值),然后继续到下一个节点。不过寻找下一个节点的时候会有两种选择,即当前节点的左子节点和右子节点。所以你应该对左右子节点都做同样的事情。但你在这里有三个不同的选择:
先打印目前节点的值,然后打印相连的左子节点,最后是右子节点;
先打印相连的左子节点,然后打印目前节点的值,最后是右子节点;
先打印相连的左子节点,然后打印右子节点的值,最后是目前节点。
// struct TreeNode {
// T item;
// TreeNode* left;
// TreeNode* right;
// }
// you cann pass a callback function to do whatever you want to do with the node's value
// in this particular example we are just printing its value.
// node is the "starting point", basically the first call is done with the "root" node
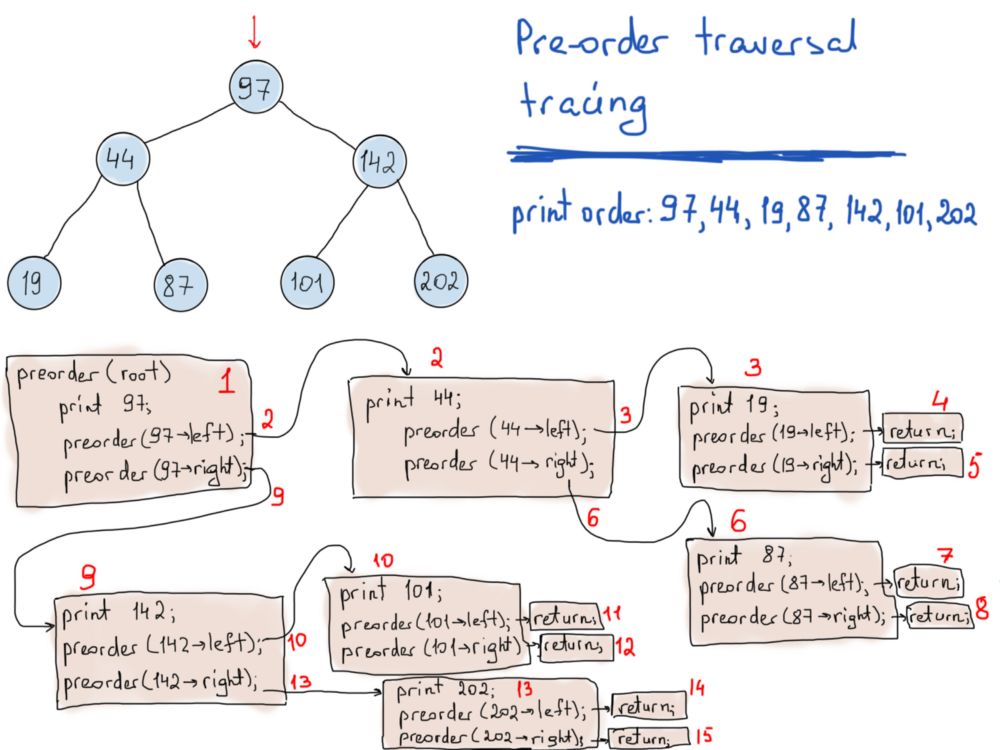
void PreOrderTraverse(TreeNode* node)
{
if (!node) return; // stop
std::cout << node->item;
PreOrderTraverse(node->left); // do the same for the left sub-tree
PreOrderTraverse(node->right); // do the same for the right sub-tree
}
void InOrderTraverse(TreeNode* node)
{
if (!node) return; // stop
InOrderTraverse(node->left);
std::cout << node->item;
InOrderTraverse(node->right);
}
void PostOrderTraverse(TreeNode* node)
{
if (!node) return; // stop
PostOrderTraverse(node->left);
PostOrderTraverse(node->right);
std::cout << node->item;
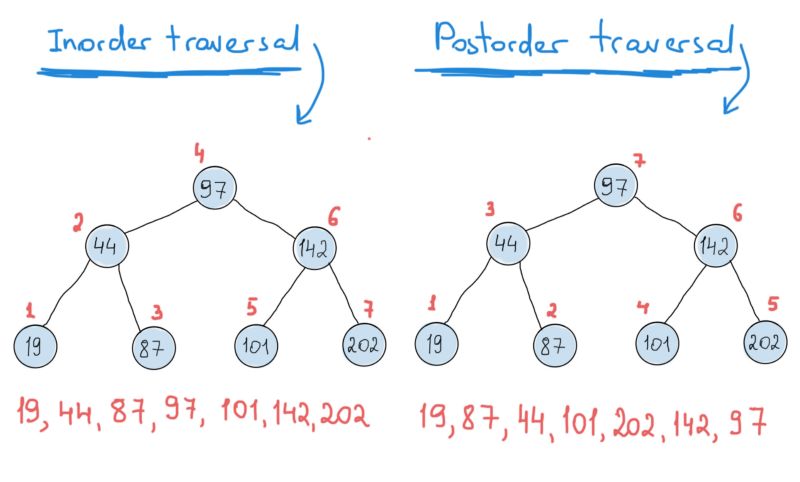
显然,递归函数看起来非常优雅,虽然它们的运行时间一般都很长。 每次递归调用函数时,这意味着我们需要调用一个完全新的的函数(参见上图)。
“新”的意思是,我们应该给函数参数和局部变量分配另一个堆栈存储空间。 这就是为什么递归调用在资源上显得很昂贵(额外的堆栈空间分配和多个函数调用)而且比较危险(需要注意堆栈溢出)。
因此相比之下更建议通过迭代法来实现同样的功能。 在关键任务系统编程(比如飞行器或者NASA探测器)中,递归是完全禁止的(这个只是传言,并没有实际数据或者经验证明这一点)。
Netflix和亚马逊个性化推荐实例:倒排索引
假设我们要将所有Netflix影片存储在二叉搜索树中,并将影片的标题作为排序键。
在这种情况下,无论何时用户输入开头为“Inter”的内容,程序都会返回一系列以“Inter”开头的电影列表,例如[Interstellar星际穿越,Interceptor截击战,Interrogation of Walter White绝命毒师]。
如果这个程序可以找出标题中包含“Inter”的所有电影(包括并没有以“Inter”开头,但是标题中包含这个关键字的电影),并且该列表将按电影的评分或与该特定用户相关的内容进行排序就更好了(例如,某用户更喜欢惊险片而不是戏剧)。
这个例子的重点在于对二叉搜索树进行有效的范围查询。但和之前一样,在这里我们不会继研究冰山还没露出的部分。
基本上,我们需要通过搜索关键字进行快速查找,然后获得按关键字排序的结果列表。其实这很可能就是电影评分或基于用户个性化数据的内部排名。 当然,我们会尽可能坚持KISK原则(Keep It Simple,Karl)。
“KISK”或““let’s keep it simple”或“for the sake of simplicity”,这简直就是教程编写者从真实问题中找一些抽象化的简单的例子,并以伪代码形式来讲解的超级借口。这些事例的解决方案简单到往往在祖父母一辈的电脑上都能运行。
这个问题也可以很容易应用到亚马逊的商品搜索中,因为用户通常通过在亚马逊上输入他们感兴趣的内容(如“图算法”)来查找相关产品,并得到以商品评分排序的清单。
Netflix里有不少影片,亚马逊里有很多商品,在这里我们把影片和商品叫做“物品”,所以每当你查找“物品”时,可以联想Netflix中的电影或亚马逊的任何合适的产品。
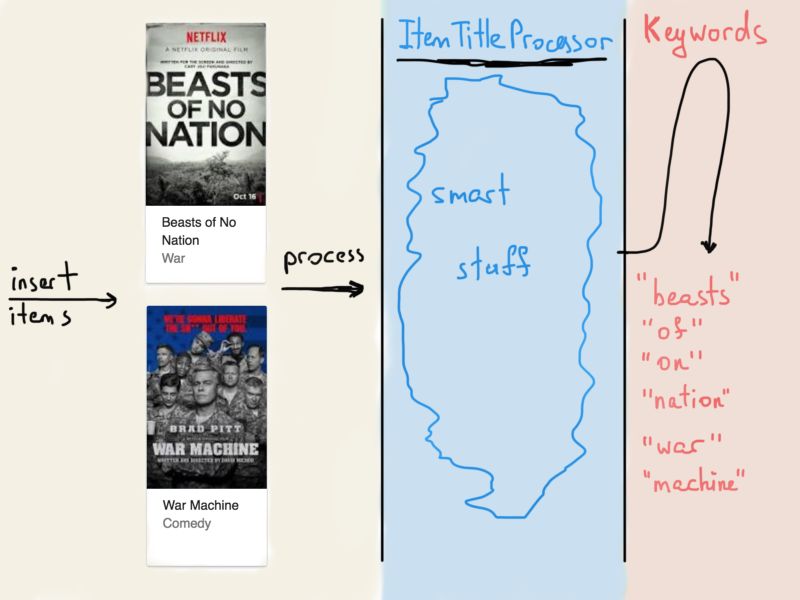
关于这些物品,最常见的就是用程序去解析标题和描述(在此我们只考虑标题)。所以如果一个操作员(比如一位通过管理板将物品数据插入Netflix / Amazon数据库的员工)把新项目插入到数据库里,物品的标题就被一些被叫做“ItemTitleProcessor”的程序处理,从而产生一系列关键字。
每个物品都有一个唯一的ID,这个ID和物品标题中的关键字有直接关联。这是搜索引擎在爬全球各种各样的网站时所做的事。他们分析每个文档的内容,对其进行标记(将其分解为更小的词组和单词)并添加到列表中。
这个表将每个标记(单词)映射到已被标记成 ”包含这个标记” 的文档或网站的ID上。
因此,无论何时搜索“hello”,搜索引擎都会获取映射到关键字“hello”的所有文档。现实中这个过程非常复杂,因为最重要的是搜索的相关性,这就是为什么Google很好用。Netflix /亚马逊也会用类似的表。同样的,读者们请在看到物品(item)时想想电影或网购的商品。
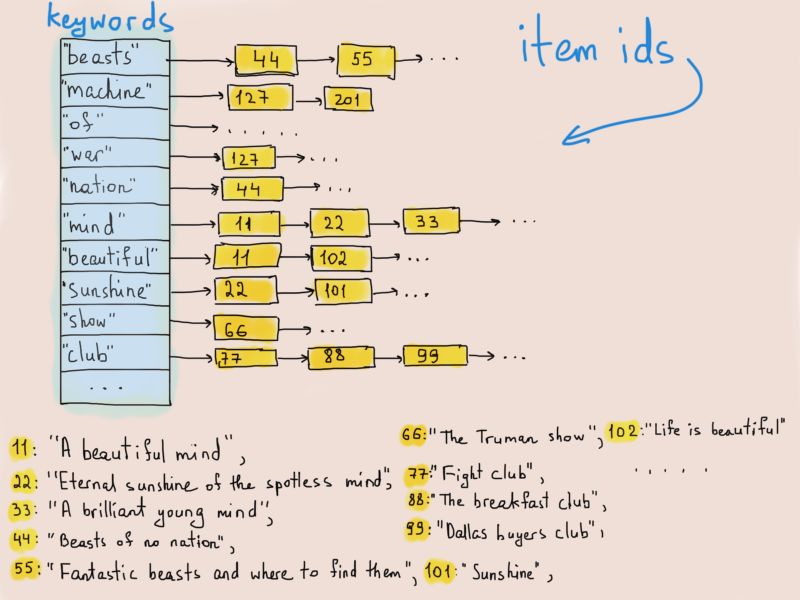
倒排索引
又来了,哈希表。是的,我们将为这个倒排索引(索引结构存储了一个和内容相关的映射)保留一个哈希表。哈希表会将关键字映射到构成二叉搜索树的许多物品当中。
为什么选择二叉搜索树呢? 这是因为我们希望可以保持物品的排序,并同时对按顺序排好的部分进行处理(响应网页前端的请求),例如请求分页时的100个项目。
这并不能说明二叉搜索树的强大功能,但假设我们还需要在搜索结果中进行快速查找,例如,你想要查找关键字为“机器”(machine)的所有三星电影。
这里需要注意的是,在不同的树中同一个物品重复出现并没有问题,因为通常用户可以使用多个不同的关键字找到同一个物品。我们将使用如下定义的物品进行操作:
我们将使用下面提到的这个方法运行程序:
// Cached representation of an Item
// Full Item object (with title, description, comments etc.)
// could be fetched from the database
struct Item
{
// ID_TYPE is the type of Item's unique id, might be an integer, or a string
ID_TYPE id;
int rating;
};
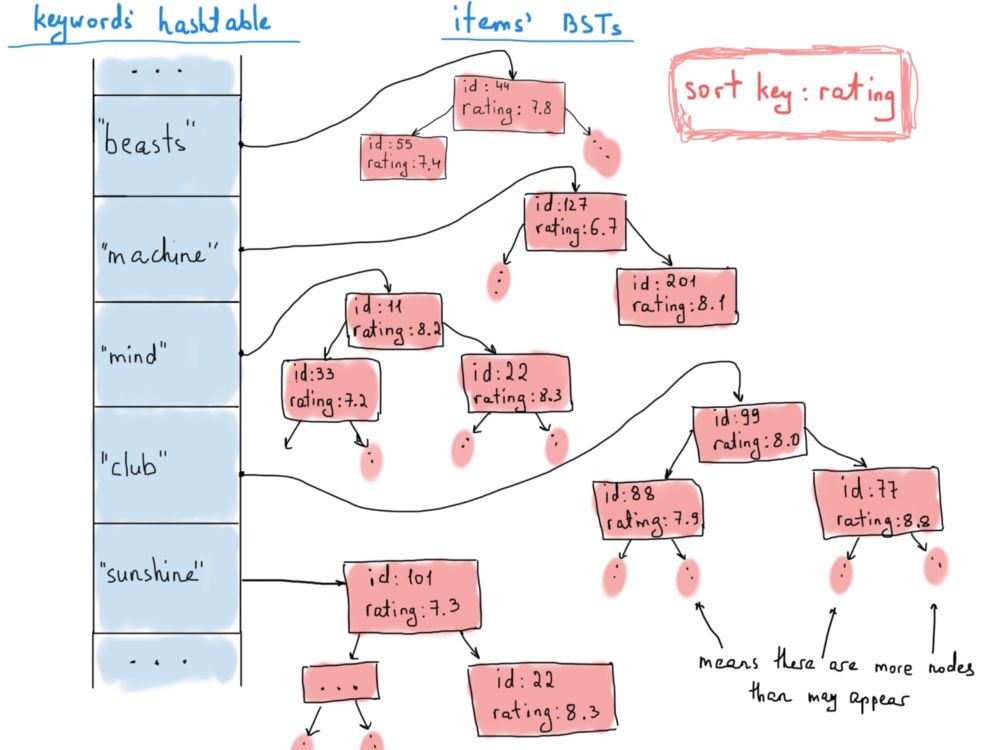
每次将新物品插入数据库时,它的标题都会被处理,并添加到总索引表里,该表会创建一个从关键字到对应物品的映射。
可能有很多物品共享相同的关键字,因此我们将这些项目保存在按照评分排序的二叉搜索树中。当用户搜索某个关键字时,他们会得到按评分排序的物品列表。我们如何从排序了的树中获取列表呢?答案是通过中序遍历。
// this is a pseudocode, that's why I didn't bother with "const&"'s and "std::"'s
// though it could have look better, forgive me C++ fellows
vector<Item*> GetItemsByKeywordInSortedOrder(string keyword)
{
// assuming IndexTable is a big hashtable mapping keywords to Item BSTs
BST<Item*> items = IndexTable[keyword];
// suppose BST has a function InOrderProduceVector(), which creates a vector and
// inserts into it items fetched via in-order traversing the tree
vector<Item*> sorted_result = items.InOrderProduceVector();
return sorted_result;
}
下面这段代码实现中序遍历:
template <typename BlaBla>
class BST
{
public:
// other code ...
vector<BlaBla*> InOrderProduceVector()
{
vector<BlaBla*> result;
result.reserve(1000); // magic number, reserving a space to avoid reallocation on inserts
InOrderProduceVectorHelper_(root_, result); // passing vector by reference
return result;
}
protected:
// takes a reference to vector
void InOrderProduceVectorHelper_(BSTNode* node, vector<BlaBla*>& destination)
{
if (!node) return;
InOrderProduceVectorHelper_(node->left, destination);
destination.push_back(node->item);
InOrderProduceVectorHelper_(node->right, destination);
}
private:
BSTNode* root_;
};
但是!首先我们首先需要评分最高的项目,而中序遍历首先输出的是评分最低的项目。这个结果和中序遍历的性质有关,毕竟从低到高的中序遍历是自下而上的。
为了得到理想的结果,即列表按降序而不是升序排列,我们应该仔细研究一下中序遍历的实现原理。 我们所做的是通过左节点,然后打印当前节点的值,最后是右节点。
正因为我们一直从左开始,所以最先的得到的是“最靠左”的节点,也就是最左节点,这是在整个二叉树里具有最小值的节点。因此,简单地将遍历方法改成右节点优先,就可以得到降序排列的列表。
和其他人一样,我们可以给这种方法命名,比如“reverse in-order traversal”,反序遍历。现在我们来更新一下之前写的代码(这里引入单个列表,注意,前方bug出没):
// Reminder: this is pseudocode, no bother with "const&", "std::" or others
// forgive me C++ fellows
template <typename BlaBla>
class BST
{
public:
// other code ...
vector<BlaBla*> ReverseInOrderProduceVector(int offset, int limit)
{
vector<BlaBla*> result;
result.reserve(limit);
// passing result vector by reference
// and passing offset and limit
ReverseInOrderProduceVectorHelper_(root_, result, offset, limit);
return result;
}
protected:
// takes a reference to vector
// skips 'offset' nodes and inserts up to 'limit' nodes
void ReverseInOrderProduceVectorHelper_(BSTNode* node, vector<BlaBla*>& destination, int offset, int limit)
{
if (!node) return;
if (limit == 0) return;
--offset; // skipping current element
ReverseInOrderProduceVectorHelper_(node->right, destination, offset, limit);
if (offset <= 0) { // if skipped enough, insert
destination.push_back(node->value);
--limit; // keep the count of insertions
}
ReverseInOrderProduceVectorHelper_(node->left, destination, offset, limit);
}
private:
BSTNode* root_;
};
// ... other possibly useful code
// this is a pseudocode, that's why I didn't bother with "const&"'s and "std::"'s
// though it could have look better, forgive me C++ fellows
vector<Item*> GetItemsByKeywordInSortedOrder(string keyword, offset, limit) // pagination using offset and limit
{
// assuming IndexTable is a big hashtable mapping keywords to Item BSTs
BST<Item*> items = IndexTable[keyword];
// suppose BST has a function InOrderProduceVector(), which creates a vector and
// inserts into it items fetched via reverse in-order traversing the tree
// to get items in descending order (starting from the highest rated item)
vector<Item*> sorted_result = items.ReverseInOrderProduceVector(offset, limit);
return sorted_result;
}
就是这样,我们可以快速提供物品的搜索结果。 如上所述,倒排索引主要用于Google之类的搜索引擎。
尽管Google是个特别复杂的搜索引擎,但它确实使用了一些简单的想法(虽然用非常现代化的方法实现),以将搜索查询与物品文档进行匹配,并尽可能快地提供搜索结果。
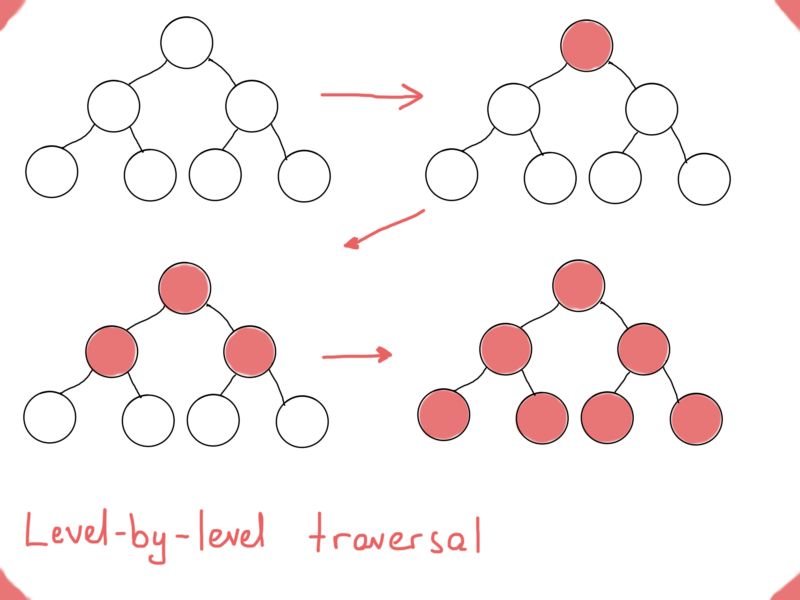
这里,我们用了树的遍历来按照某种排序来处理搜索结果。在这一点上,先序、中序和后序遍历看起来可能绰绰有余,但有时还需要另一种类型的遍历。大家可以试着解决这个众所周知的编程面试题“如何逐层打印一个二叉树?”:
深度优先搜索DFS和广度优先搜索BFS
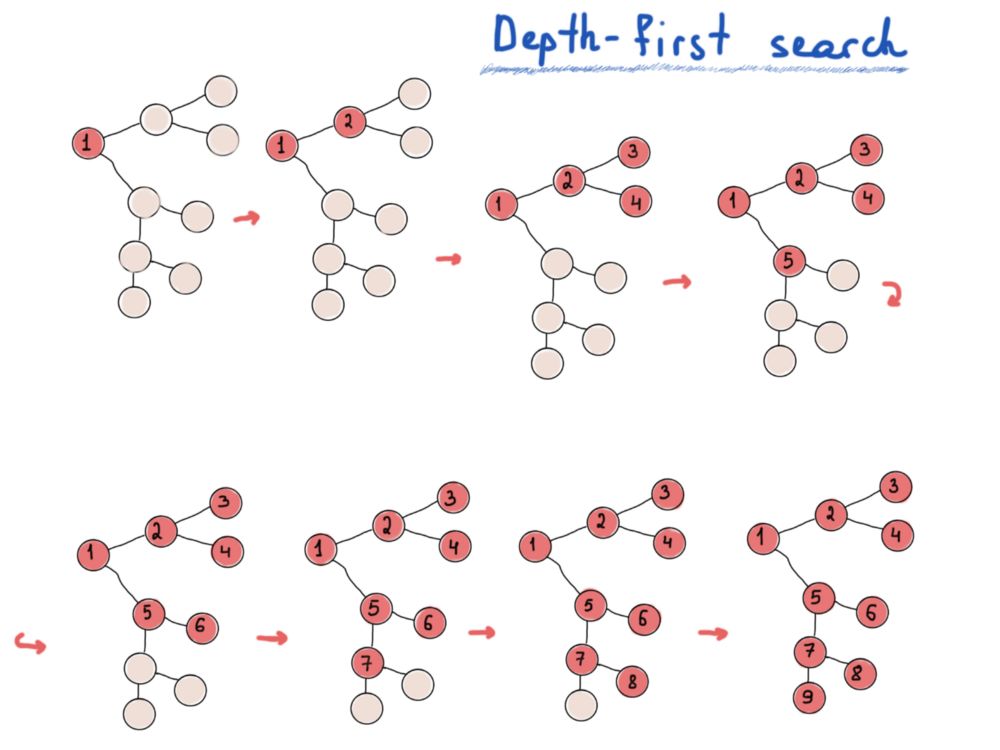
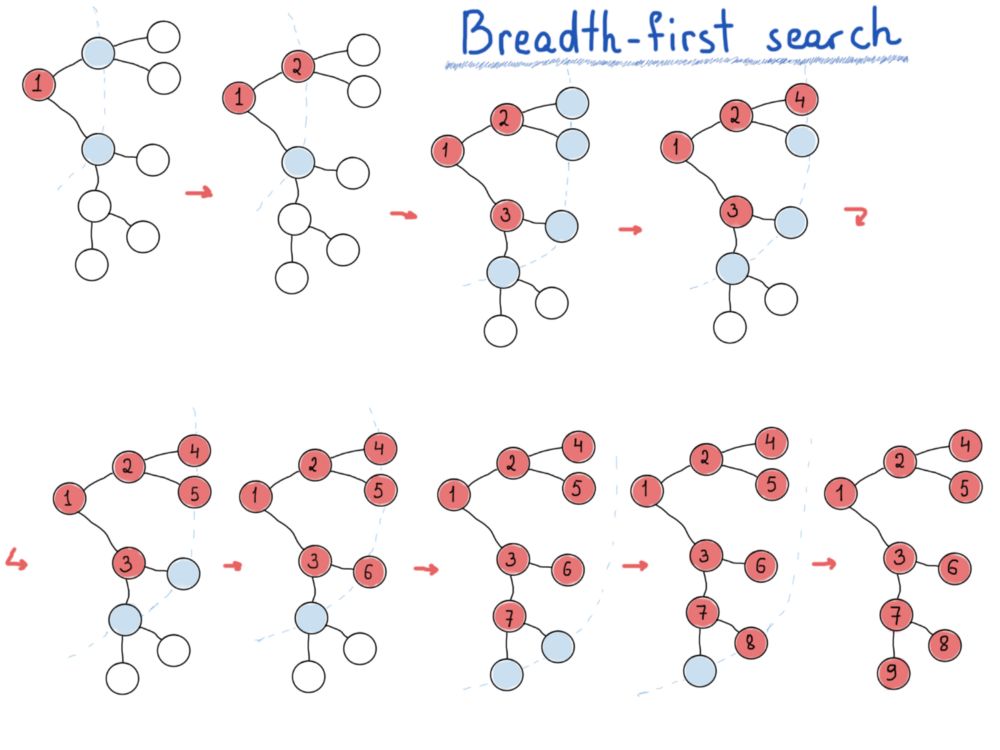
如果你对这个问题不熟悉,请想一下遍历树时用来存储节点的数据结构。如果我们拿逐层树遍历和先序遍历、中序遍历、后序遍历比较,最后会得到两种主要的图遍历方法,深度优先搜索(DFS)和广度优先搜索(BFS)。
深度优先搜索寻找最远的节点,广度优先搜索先探索最近的节点。
深度优先搜索:做的多,想的少。
广度优先搜索:先四处观望再进行下一步动作。
DFS很像先序遍历、中序遍历、后序遍历,而BFS可以逐层遍历节点。为实现BFS,需要一个队列(数据结构)来保存图的“层次”,同时打印(访问)其“父母层”。
上图中,放入队列的节点为浅蓝色。基本上逐层进行,每层节点都从队列中获取,访问每个获取的节点时,将其子节点插入到队列中(用于下一层)。下面的代码非常简单,很好地说明了BFS的思路。假设图是连通图,可以修改以适用于非连通图。
// Assuming graph is connected
// and a graph node is defined by this structure
// struct GraphNode {
// T item;
// vector<GraphNode*> children;
// }
// WARNING: untested code
void BreadthFirstSearch(GraphNode* node) // start node
{
if (!node) return;
queue<GraphNode*> q;
q.push(node);
while (!q.empty()) {
GraphNode* cur = q.front(); // doesn't pop
q.pop();
for (auto child : cur->children) {
q.push(child);
}
// do what you want with current node
cout << cur->item;
}
}
这一思路对基于节点的连通图表示非常简单。请记住,对于不同表示,图遍历的实现也不相同。BFS和DFS是解决图搜索问题的重要方法(但记住图搜索算法有很多很多)。
虽然DFS是优美的递归实现,但迭代实现也可行的。而BFS的迭代实现我们会用一个队列,对DFS需要一个堆栈。图论中的一个热门问题,是找节点间最短路径。来看最后一个例子。
Uber最短路线实例
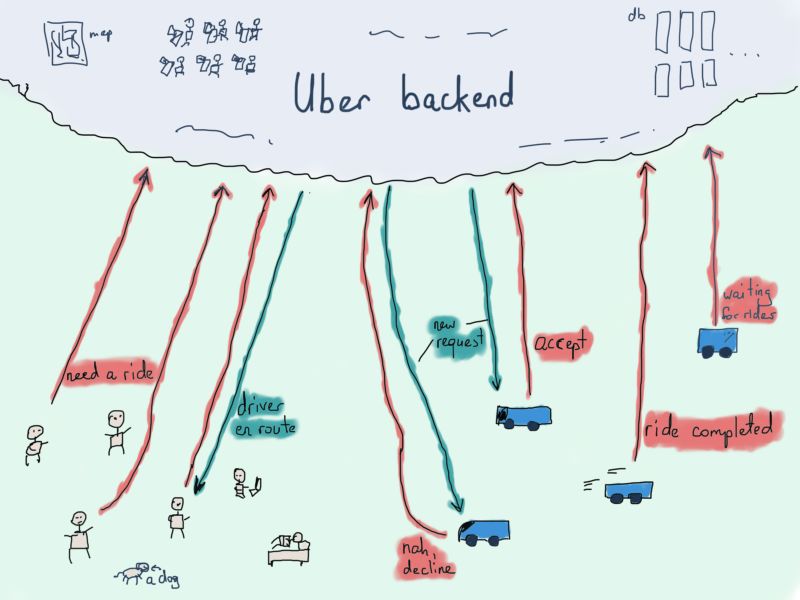
Uber有5000万乘客和700万司机,所以高效地将司机与乘客进行匹配非常重要。司机使用Uber司机专用应用来接单,乘客就用Uber应用叫车。
首先是定位。后台需要处理数百万条乘客请求,并发送给附近的司机,通常会发送给多个司机。虽然将乘客请求发送给附近所有司机看起来更简单,甚至有时候也更有效,但是进行一些预处理往往效果更好。
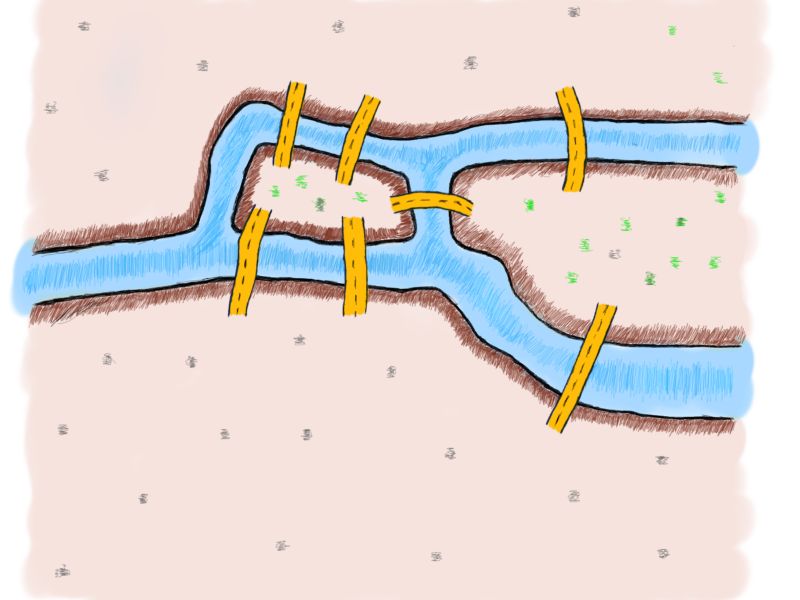
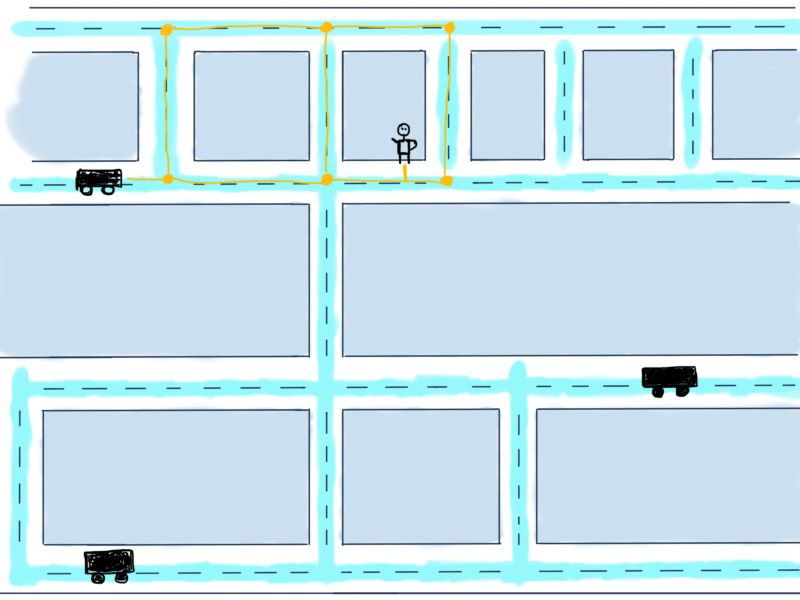
除了处理收到的请求,根据乘客坐标查找定位区域,进而查找坐标最近的司机外,还需要为乘客找到合适的司机。假设已经有了包含乘客及几个附近车辆的小地图,(已经对比了车辆当前坐标和乘客坐标,并确定了附近车辆,这一过程称为地理信息处理),小地图如下:
车辆到乘客的可能路线用黄色标出。那么现在的问题是计算从车辆到乘客需要的最小距离,也就是说,要找到最短路线。虽然这个问题更像Google地图而不是Uber应该考虑的,但我们还是要解决这个简化的问题,因为通常乘客附近有多辆车,Uber需要计算距离最近且评分最高车辆发送给乘客。
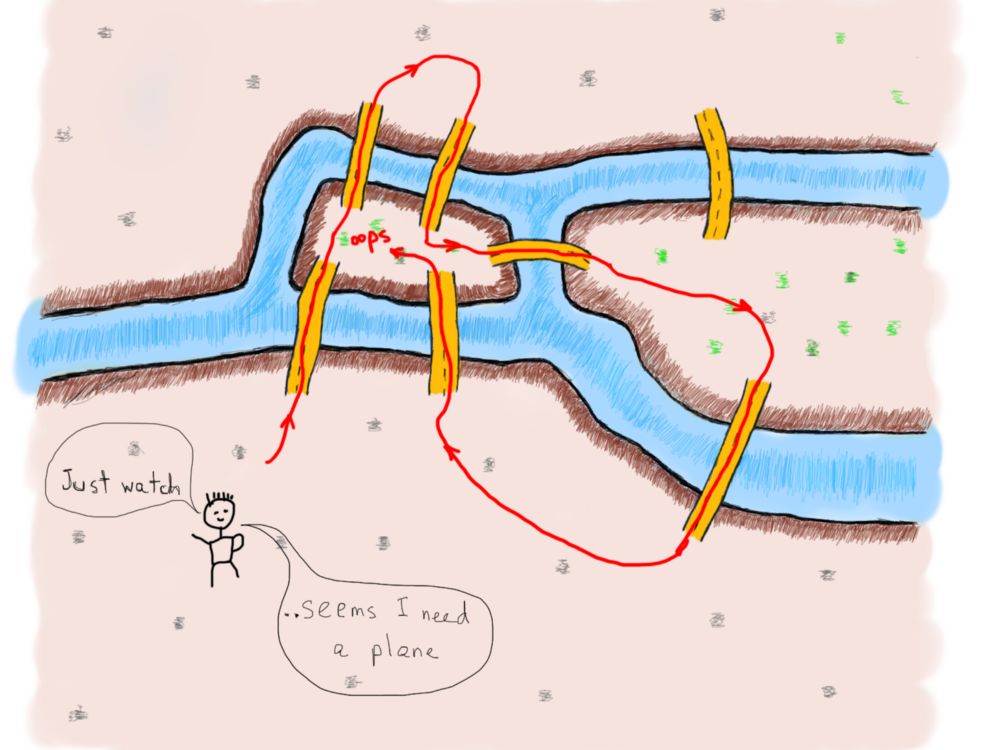
对于上图而言,要分别计算三辆车抵达乘客的最短路线,再决定哪辆车是最佳选择。为简化问题,这里讨论只有一辆车的情况。以下标出三条抵达乘客的路线。
抵达乘客的可能路线
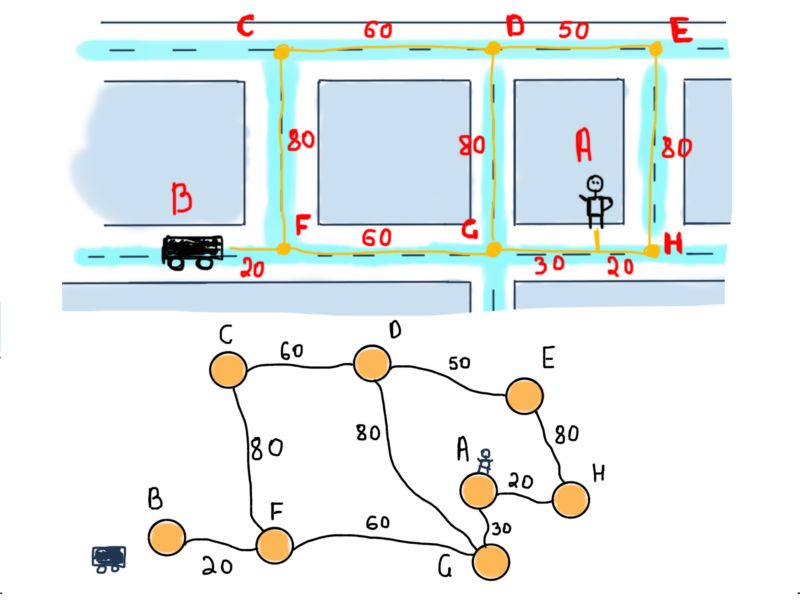
接下来进入重点,先将小地图抽象成图:
这是无向加权图(确切地说是边加权图)。为了找到顶点B(汽车)和A(乘客)之间的最短路径,应该找包含尽可能小的权重的边的路径。我们用Dijkstra版本;你也可以自行设计你的方案。以下是Dijkstra算法的维基百科。
将开始的节点称为起始节点。Y节点的路径长度定义为从出发点到Y点的总路径长度。Dijkstra算法将会分配一些初始距离值然后逐步改善它们。
1.将所有节点设为未访问。设置一个包含所有未被访问节点的集合,称为未访问集合。
2. 对所有顶点的路径长度赋暂定值:将起始节点的路径长度设为0,所有其他顶点的路径长度设为无穷大。将起始节点设为当前节点。
3.对于当前节点,考虑其周围所有未访问的相邻节点,并且计算通过当前节点到它们的暂定距离。将新计算得到的暂定距离与当前分配的距离进行比较并选择较小的值然后分配。例如,如果当前节点A的距离为6,连之相邻B的长度为2,则通过A到B的距离将为6 + 2 = 8。如果B先前被标记的距离大于8,则将其更改为8.否则,则保持当前值。
4.当我们考虑完当前节点的所有相邻节点时,将当前节点标记为已访问并将其从未访问节点集中移除。被访问的节点将不会再次被查看。
5.如果目标节点已经被标记为已访问(当目标是两个特定节点之间的路径)或者未访问集合中的节点之间的最小暂定距离是无穷大时(目标完全遍历时;发生在初始节点和剩余的未访问节点之间没有连接时),将会停止。算法已经完成。
6.否则,选择未访问过的并且具有最小暂定距离的节点,把它作为新的“当前节点”,然后回到步骤3。
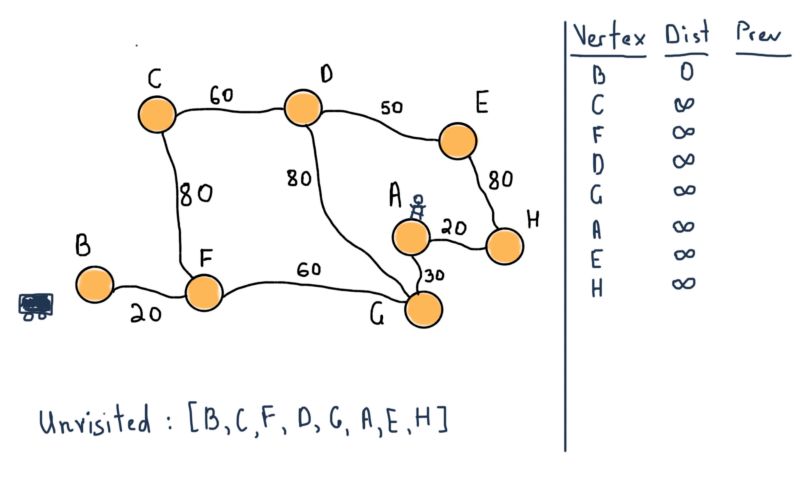
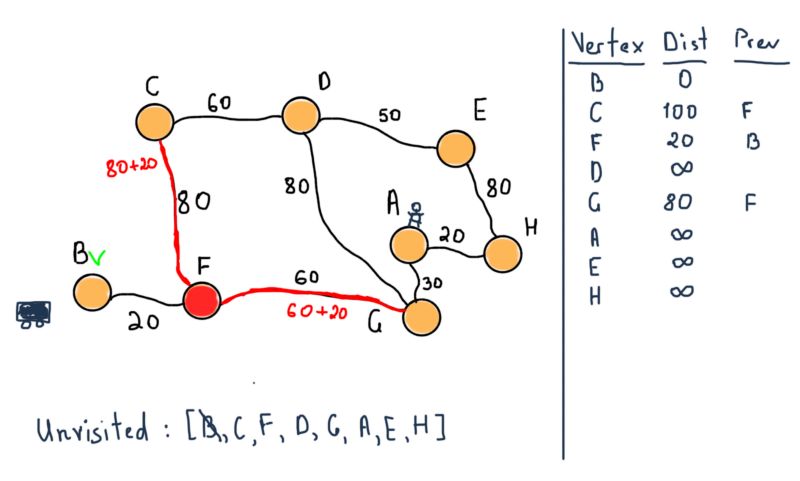
应用Dijkstra算法到示例中,顶点B(车)是起始节点。前两步如下:
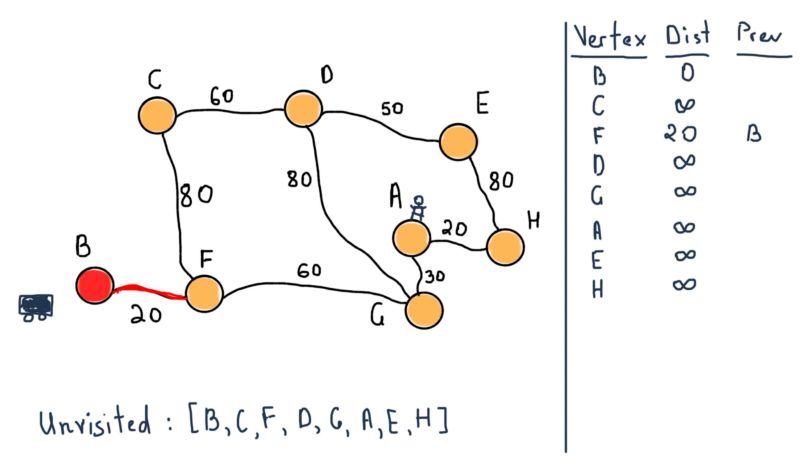
所有的节点都属于未访问集合,需要注意图示右侧的表格。对于所有节点,它将包含从B到前一个(标记为“Prev”)节点的所有最短距离。例如,从B到F的距离是20,前一个节点是B。
将B标记为已访问,然后移动到它的相邻节点F。
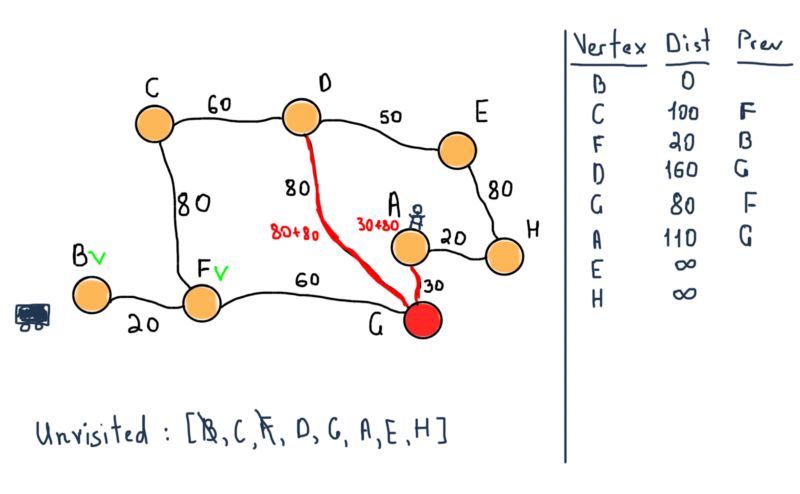
现在将F标记为已访问,并选择具有最小暂定距离的点为下一个未访问节点,即G。依然需要注意左侧的表格,在前面的图例中,节点C,F和G已经将它们的暂定距离设置为通过之前所提到的结点的距离。
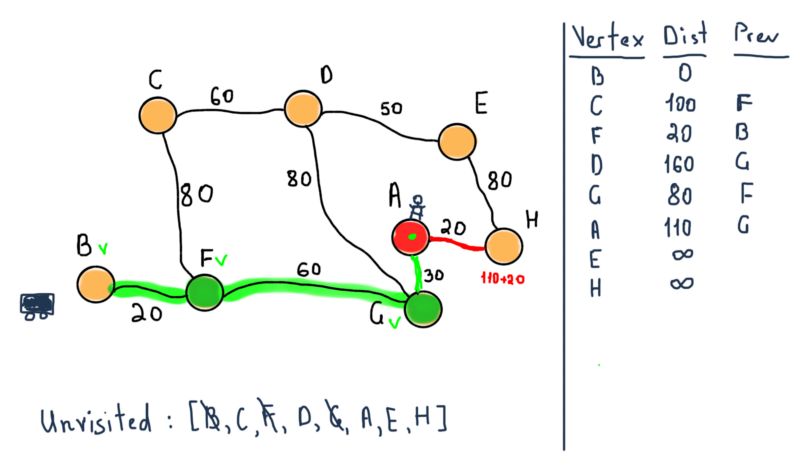
如同算法阐述的那样,如果目标节点被标记为已访问(在我们的例子中,当要两个特定节点之间的路径时),那我们可以结束算法了。因此,下一步终止算法返回下面的值。
所以我们既有从B到A的最短距离又有通过F节点和G节点的路径。
这是Uber中的一个再简单不过的例子,只是沧海一粟。然而,这是很好的起点,可以帮你迈出探索图论应用的第一步。
关于图论还有很多内容有待研究,这篇文章只是冰山一角。读到最后的你非常棒,奖你一朵小红花,别忘了点赞和分享哟,谢谢。
原文链接:
https://medium.freecodecamp.org/i-dont-understand-graph-theory-1c96572a1401
【今日机器学习概念】
Have a Great Definition
志愿者介绍