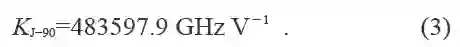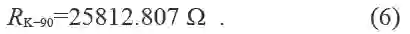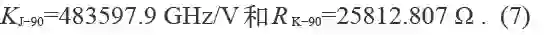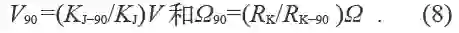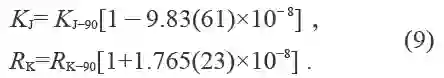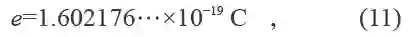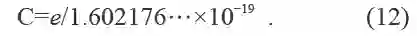基本电荷的精密测量及电流单位安培的重新定义

作者：沈乃澂 (中国计量科学研究院)

摘要 1990年1月1日，为了建立电压和电阻及其他电学量在测量中的国际一致性，国际计量委员会引入了分别基于约瑟夫森效应和量子霍尔效应的伏特V和欧姆Ω新的实际表示，以及KJ和RK的约定值(即采用值)。本文给出了由国际科技数据委员会推荐的2014年电学量基本常数自洽组的最新数值。

关键词 精密测量，约瑟夫森效应，量子霍尔效应，安培，伏特，欧姆

1 电流单位的定义

1948 年1 月1 日采用电流单位的绝对单位制。这个单位制的基础是1901 年由意大利科学家乔吉(G. Giorgi)^[1]提出的修正的CGS制。这个单位制又称为米—千克—秒—安培单位制(简称MKSA制)。MKSA 制的单位量值大小很适合于实际测量，从安培的定义中消除了不方便的4π因子。第九届国际计量大会(CGPM)批准的是用两个平行导体之间的力定义安培；伏特是在流过1 A恒定电流的导线内，两点之间所消耗的功率为1 W时，两点之间的电位差，即在导体间加1 V的恒定电位差产生1 A的恒定电流的电阻。大会对其他单位也作了定义，并都采用了国际单位制(SI)，1960 年第11 届CGPM正式批准，指定安培为电学量的基本单位。

然而，安培的定义并不宜于实际复现，因此继续在国际计量局(BIPM)开展国际比对，并采用协定将BIPM 标准的值作为伏特和欧姆。1970年，十几个国家实验室送它们的标准到BIPM，进行每三年一次的国际比对：欧姆数值的分散性约为1×10^-6，伏特数值的分散性约为欧姆数值分散性的两倍或三倍。从结果来看，国家实验室有时已调整了它们标准的值，BIPM 在1968 年也进行了调整。

2 电学单位的量子计量——约瑟夫森效应和量子霍尔效应

2.1 约瑟夫森的贡献

1962 年，英国理论物理学家约瑟夫森(图1)研究两块超导体之间的结的性质，这个结后来被称为约瑟夫森结^[2]。他计算了超导结的隧道效应并得出结论：如果两个超导体距离足够近，电子可以作为一种辐射波穿透超导体之间的极薄绝缘层而形成电流，而超导结上并不出现电压；如果超导结上加有电压，电流就停止流动并产生高频振荡。这就是约瑟夫森效应。

图1 英国物理学家约瑟夫森(1940— )

约瑟夫森效应是指电子对通过两块超导体间的薄绝缘层(厚度为1 nm)时发生的量子力学隧道效应。1962 年，英国剑桥大学年仅22 岁的研究生B. D. 约瑟夫森从理论上预言，当超导电子对通过超导体—氧化层—超导体的薄夹层结构时形成无损耗的超流电流，即超导电子对的隧道效应。1963 年，美国贝尔实验室的科学家从实验上证明了约瑟夫森的预言，故称约瑟夫森效应。由此，一门新的学科——超导电子学创立。尤其是伴随着根据约瑟夫森效应原理制成的超导量子干涉器件(SQUID)的问世，相应的超导体的另一大类应用，即弱电(弱磁)应用也拉开了序幕。约瑟夫森由于预言隧道超导电流的存在而获得1973 年诺贝尔物理学奖。

1962 年，约瑟夫森预言^[2]，如果两个超导体用薄的绝缘间隙相连接，并用频率为f 的微波辐照，所加的直流电压将产生一电流，其电流—电压特性具有下式给出的电压阶梯

式中h 是普朗克常数，e 是电子电荷。这使计量实验室产生了很大的兴趣，因为这清晰地表示了一个用频率及基本常数准确地测定电压的方法。其中的困难是，我们对常数的认识还不如可以比对的电压标准那样精密。但是，如果我们将关系式写为

式中K_J是约瑟夫森常数，具有一个认为正确的数值，现在还不是用绝对方法，提供了一个监测电压标准的有效方法，而无需输运的韦斯顿电池来进行比对。许多国家实验室用它们的电压来测量约瑟夫森常数，并用其监测电压标准。在1972 年的会议上，电学咨询委员会(CCE)注意到这些进展而决定，1969 年1 月1 日的BIPM 电压V69-BI，在百万分之一的一半的精度内， 等于频率为483594.0 GHz的波辐照在结上时约瑟夫森效应所产生的电压。并不是所有的国家都采用了这个数值，因为显然实际上与SI 值并不一致。1986 年，CCE确定一个工作组，来评价这项证据，并在此后推荐下列数值

于1990 年1 月1 日起采用，并可能在检测国家标准时使用，其不确定度估计为4×10^-7。CCE作此决定，显然这表示了一个参考标准，并不意味单位的SI 定义或基本常数的数值有任何变化。它表达了下列观点，在可预见的未来一段时间内推荐值不变将是必要的。

一个实际问题是，由约瑟夫森结产生的小电压——例如，对5 GHz 的频率约为10 mV。这使得监视1V标准不很容易，但NIST 的工作在串联中有20000个结的阵列，由此解决了这个问题。

2.2 冯·克利青的贡献

冯·克利青(图2)是德国物理学家，生于德国波森的希罗达(今属波兰)，1972 年获维尔茨堡大学博士学位，先后在该大学物理研究所、法国格勒诺布尔的普朗克研究所工作。在研究半导体霍尔效应的过程中，1980 年冯·克利青和他的合作者在霍尔电阻随栅极电压变化的曲线上观察到霍尔电阻平台^[3]。霍尔电阻对磁场成阶梯变化，其电阻值由物理常数h/e²除以整数值n (n=2，3，4，5，6，8，10)获得。这一结果称为量子霍尔效应。通过它可以精确地测定精细结构常数α。由于发现量子霍尔效应，冯·克利青获得1985 年诺贝尔物理学奖。

图2 德国物理学家冯·克利青(1943— )

2.3 量子霍尔效应的物理意义

量子霍尔效应是霍尔电阻以量子化形式变化的现象。整数量子霍尔效应是在某些人造的二维半导体结构中，电子气限制在极薄的一层之内运动，在垂直层面方向施加强磁场，在层面与电流I相垂直的方向上出现电势差V_H，称为霍尔电压，R_H=V_H/I 称为霍尔电阻。经典霍尔效应表明，R_H随所加磁场的磁感强度B 增加而增加，呈线性关系。1980 年冯·克利青在1.5 K测量这种半导体结构的霍尔电阻，发现R_H与B的关系是在总的直线趋势上出现一系列平台，R_H =h/ie²，这里i 是正整数，h为普朗克常数，e为电子电荷。该现象称为整数量子霍尔效应。i=1时，量子霍尔电阻值为h/e²，等于25.8128 kΩ，称为冯·克利青常数。实验上霍尔电阻的各个量子化值都极为精确。1990 年1 月1 日起，国际计量组织选用量子霍尔电阻作为电阻计量标准。量子霍尔效应提供了一种独立于量子电动力学的凝聚态物理实验方法来测量自然界的基本常量——精细结构常数α = e²/2ε₀hc，其中c为真空光速，h为普朗克常数， ε₀ 是真空电容率。

量子霍尔效应的实质是在强磁场中电子的运动形态发生变化，由具有一定速度的直线运动变为在垂直磁场平面中的圆周运动，与之相应电子能谱发生改组：由自由运动的准连续谱变为反映圆周运动的朗道能级E_n=(n+1/2)ω_c，式中ω_c=eB/(mc)是圆周运动的角频率，其中m为电子的有效质量，n=0，1，2，……因此能级间距大小由磁场决定，当电子气正好填满i 个朗道能级时，霍尔电阻R_H=h/ie²。

在平面中有同样半径的圆周轨道具有相同的能量，属于同一朗道能级。为了保证电子在做圆周运动时不被散射，应满足的条件是ω_cτ≥1，这里τ 是电子相继两次散射间的平均自由时间，所以只有在强磁场及低温下( τ 可较大)才能实现量子霍尔效应的观测。

监视欧姆基本上是类似的。如果一个半导体在与磁场呈直角的方向上载有电流I，对两者呈直角处产生的电压为V_H。这是熟知的霍尔效应，其比值

是熟知的霍尔电阻。通常，这与场的几何形状和强度有关，但1980 年冯·克里青说明了，在确定的半导体内，有效地限于二维的霍尔电阻的电流是量子化的，其值为

其中i=1，2，3，……(与场强有关)，R_K是一个常数，即熟知的冯·克里青常数。它的理论值是h/e²。用这个效应，可能建立一个用于监视国家欧姆的电阻标准。如同约瑟夫森效应，这个装置并不简单——例如，它必须在液氦温度下运行——因此很难作为日用参考标准，但对于在高水平下作为比对是很有用的，它不需要进行搬运。

1986 年，CCE建立了另一个工作组来考虑量子霍尔效应。在1988 年的报告后，CCE推荐冯·克里青常数将从1990 年1 月1 日起监视国家欧姆的数值，这个常数的数值为

CCE再次强调指出，这并不意味着单位定义的任何变化，或h 和e 的数值的变化，而只是一个参考值，在可预见的未来似乎可以不变。

为了国际统一，首先要将公认的BIPM 保存的实物基准与绝对测量的结果相比较，绝对测量值取各国结果的最小二乘平差值。通过比较得出BIPM 保存值与理论定义值相接近的程度，由此定出该基准器的数值。各国再根据它定出本国主基准器的值，从而保证了国际测量数据的统一，也是国际贸易往来和交流的需要。

在复现电学单位的历程中，并未找到一项技术可以将SI 电学单位的不确定度达到2×10^-8。应该注意到，为了复现SI 电学单位对机械装置有极高的要求。至今，由于宏观量子效应的出现，使电学量可以与相关的基本物理常数相链接。安倍的定义要求磁常数μ₀=4π×10^-7Hm^-1，而基于量子效应的单位是根据R_K-90和K_J-90约定值导出的，因为它们的SI 真值并不精确知道。如果在SI 单位中e和h精确已知，就可以废弃过去的R_K-90和K_J-90约定值，使以量子效应为基础的电学单位直接复现SI 电学单位。这是采用h 重新定义千克，而不采用阿伏伽德罗常数重新定义千克的主要优点。

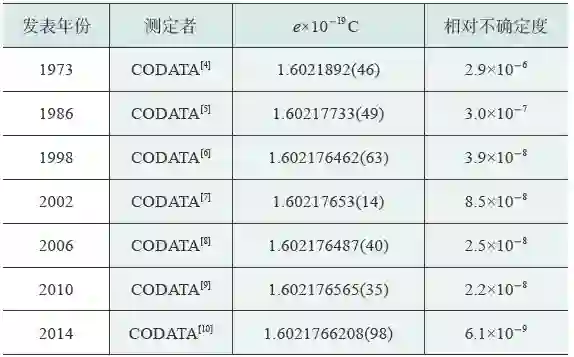
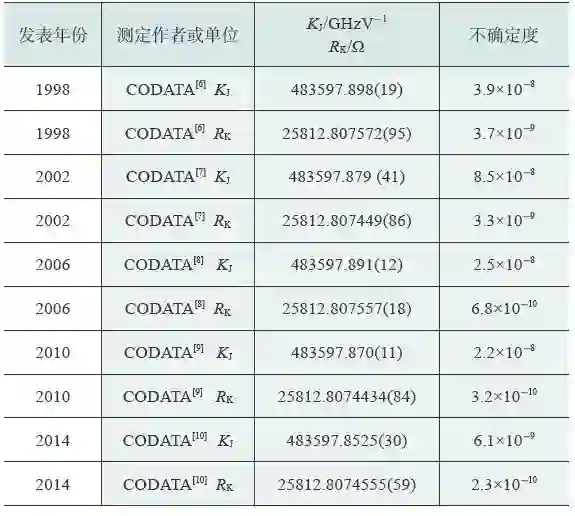
量子霍尔效应提供了电阻的普适标准，使电阻在理论上仅与普朗克常数h 和基本电荷e 有关。通常，这个标准在GaAs/AlGaAs 中执行功能，但石墨烯的电子性质有望成为更实用的装置。实验条件必须在碳化硅上用化学蒸汽沉积生成的高品质石墨烯制造的装置中运行。尤其，在磁通密度为10 T的较宽范围内，当温度升到10 K时，电流增大到0.5 mA，磁通密度降到3.5 T，霍尔电阻能准确到1×10⁻⁹的范围内。此外，量子霍尔电阻在石墨烯和GaAs/AlGaAs 之间的测量一致性表现的最终不确定度为8.2 × 10⁻¹¹，支持了量子霍尔效应的普适性。这也提供了量子霍尔电阻与普朗克常数h 和基本电荷e 的关系。表1 示出了自1973 年以来的基本电荷e 测量进展的一览表，不确定度由10^-6减小到10^-9量级。表2 示出了自1988年以来的约瑟夫森常数K_J及冯·克里青常数R_K测量进展的一览表，K_J的不确定度由10^-8减小到10^-9量级，R_K的不确定度由10^-9减小到10^-10量级。

表1 基本电荷e测量进展一览表

表2 约瑟夫森常数K_J和冯·克里青常数R_K测量进展一览表

3 2014 年CODATA 推荐值及对计量学和物理学的重要意义

1990 年对约瑟夫森常数K_J和冯·克里青常数R_K 建立的电压和电阻的约定单位所采用的约定值：

V₉₀和Ω₉₀由下式给出：

其他的约定电单位按V₉₀和Ω₉₀推算，例如：电流约定单位A₉₀=V₉₀ /Ω₉₀，功率约定单位W₉₀= A₉₀V₉₀，电容约定单位F₉₀=C₉₀/V₉₀等，2014 年平差给出了K_J与K_J−90及R_K与R_K−90之间的关系：

由上两式可导出：

上式表明，V₉₀ 大于V，Ω₉₀大于Ω。其含义是：被测电压和电阻分别可溯源到约瑟夫森效应和K_J−90及量子霍尔效应和R_K−90，相对于SI 小于相关值，但其差值对V₉₀/V 在40×10^-8 范围内，对Ω₉₀/Ω在10×10⁻⁸范围内。这是由CIPM 所属的CCEM所分配的不确定度范围。

4 用基本电荷e重新定义电流单位安培

安培A是SI 的电流单位；其量值是固定基本电荷的数值精确地等于1.602176…×10⁻¹⁹并以单位C表示。

因此，有精确关系式

或

这个定义的表述是：安培是相应于每秒流过1/(1.602176…×10⁻¹⁹)基本电荷的电流。

用h 和c 的精确值，提供了精确的约瑟夫森常数值K_J=2e/h 和冯·克里青常数值R_K=h/e²，通过约瑟夫森效应和量子霍尔效应以高精度来复现安培、伏特和欧姆以及其他电学单位， 因此消除了目前传统的非SI 单位电学单位的现存系统。

参考文献

[1] Giorgi G. Atti dell' Assoc. Elettr. Ital.，1901，5：402

[2] Josephson B D. Phys. Lett.，1962，1：251

[3] von Klitzing K et al，Phys. Rev. Lett.，1980，45：494

[4] Cohen E R，Taylor B N. J. Phys. Chem. Ref. Data，1973，2(4)：663；1973 年基本物理常数的最小二乘法平差. 沈乃澂，沈平子等译，王竹溪审校，中国计量科学院内部刊物，1975

[5] Cohen E R，Taylor B N. Rev. Mod. Phys.，1987，59(4)：1121 1986年基本物理常数国际推荐值. 沈乃澂编译，科学出版社，1987

[6] Mohr P J，Taylor B N. J.Phys. Chem. Ref. Data，1999，28：1715；基本物理常数1998 年国际推荐值. 沈乃澂编译，聂玉昕审校，中国计量出版社，2004

[7] Mohr P J，Taylor B N. Rev. Mod. Phys.，2005，77(1)：1

[8] Mohr P J，Taylor B N，Newell D B. Rev. Mod. Phys.，2008，80(2)：633

[9] CODATA Task Group on Fundamental Constants，CODATA recommended values of the fundamental physical constants，参见

the 2010 CODATA recommended values and bibliography at http：//physics.nist.gov/cuu/Constants/Citations/Search.html

[10] Ribeiro-Palau R，Lafont F，Brun-Picard J et al. Nat. Nanotechnol.，2015，10：965

本文选自《物理》2019年第4期

---

▼

往期精彩回顾

▼

1.环形正负电子对撞机：物理、技术以及现状

2.量子十问之六：量子计算，这可是一个颠覆性的新技术 | 郭光灿

3.晶体几何系列之二：平面上圆密排定理的证明

4.单纯的元素，复杂的历史

5.原位电子显微学探索固体中的离子迁移行为（一）

6.爱因斯坦的物理学成就与年谱 | 曹则贤

7.物理学：A Source of Power for Man

8.回音壁模式光学微腔传感

9.杨-米尔斯理论说了啥？为什么说这是杨振宁超越他诺奖的贡献？

10.周末讲堂——三位新晋狄拉克奖得主：开宗立派又风格迥异