【白话模型量化系列】矩阵乘法量化

会员服务 ·

【白话模型量化系列】矩阵乘法量化

2021 年 11 月 26 日 极市平台

↑ 点击蓝字关注极市平台

作者丨godweiyang

来源丨算法码上来

编辑丨极市平台

极市导读

考虑使用浮点数矩阵乘法，如何将它转化为整数矩阵乘法，并且得到几乎相同的乘法结果呢？本文对该过程进行了详细的解析。 >>加入极市CV技术交流群，走在计算机视觉的最前沿

模型量化是模型加速方向一个很重要的方法，主要思想就是用int8数据格式来存储和进行计算。这样做有两点好处：

可以减小模型存储的体积。原本float32存储需要4个字节，现在int8存储只需要1个字节，体积是原来的1/4。
可以加快计算速度。这主要是因为int8数据的读写更快，并且int8矩阵乘法一般来说会更快一点。

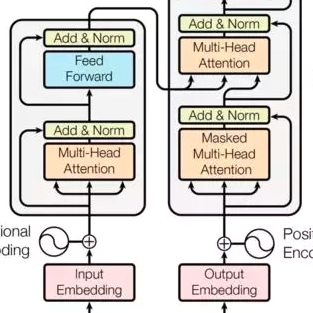
以现在最常用的Transformer模型来举例，在使用CUDA推理加速库（例如LightSeq）之后，矩阵乘法的占比高达将近90%。所以优化非矩阵乘法的速度意义不是很大了，占比不高，你算得再快对整体的提速也很小，因此可以尝试优化矩阵乘法。

那么我们考虑浮点数矩阵乘法，如何将它转化为整数矩阵乘法，并且得到几乎相同的乘法结果呢？

用整数矩阵来表示浮点数矩阵

首先我们需要将一个浮点数矩阵用整数矩阵来表示。我们假设的数值范围在之间，其实这个假设是合理的，例如一般深度学习模型参数初始化都是正态分布，那么数值范围就在之间。然后整数矩阵的数值范围其实就是有符号整数的表示范围，为了实现的简单，我们只量化到，这样就和一样关于零点左右对称了。我们令，用来表示int8的数值范围，如果，那就是int4的范围了。

接着整数矩阵就可以表示为，也就是将浮点数区间里的数字等比例映射到整数区间，然后向最近的整数取整。同理，整数矩阵可以表示为。

这样我们就可以得到两个浮点数矩阵的整数表示，接下来就可以利用他们来进行整数矩阵乘法的转换。

转化为整数矩阵乘法

整数矩阵还原为浮点数很简单，只需要即可。但是注意是取过整的，所以还原回去的并不完全等于原始的，是有误差的。举个通俗的例子，两个浮点数0.1和0.101经过量化都变成了整数13，但是还原回浮点数后全都变成了0.102，再也没法区分两个浮点数有什么不同了。

所以回到原始的问题，浮点数矩阵乘法可以改写为，也就是。

那么就可以先计算整数矩阵乘法，然后得到整数的输出矩阵之后，乘上系数，还原为浮点数矩阵。

注意输入矩阵和都是int8的，但是乘法结果一定是int32的。

总结一下流程

输入两个浮点数矩阵和，先分别转化为各自的整数矩阵和。
然后计算整数矩阵乘法结果。
最后乘上系数还原为浮点数的乘法结果。

进阶（relu激活函数）

熟悉Transformer的同学应该知道，FFN第二层输入分别是relu的结果和参数。那么这里就存在一个问题，relu结果的数值范围是，而不可能是。

如果我们强行还按照的范围来量化relu结果的话会怎么样呢？这样会导致整数区间永远不会有数字，因为根本没有负数浮点数的存在。这样就白白浪费了127个整数，就会导致量化的精度大大受损。

那按照来量化的话，怎么计算整数矩阵乘法的结果呢？

稍稍推导一下就可以得出，可以表示为，其中表示和相同形状的全1矩阵。而的话依然表示为。

这样矩阵乘法可以改写为。其中第二项因子可以用来进一步简化，最终得到。

第一项因子和之前一样，先算整数矩阵乘法，再乘上系数，只不过系数变成了。

第二项因子的维度和相同，并且它的矩阵元素等于中同一列的元素之和。那么问题就很简单了，我们只需要提前计算出矩阵每一列的元素和，再乘上系数，结果存下来。最后在计算完整数矩阵乘法结果之后，加上这个列元素之和就行了，你可以将其理解为残差项。

总结

如果矩阵乘法两个输入的范围都是关于零点对称的，那么计算公式为：
量化：

反量化：

如果矩阵乘法其中一个输入是relu的结果，那么计算公式为：
量化：

反量化：

当然还有很多其他情况，例如softmax的输出范围一定是，那么attention中的矩阵乘法公式还得改写。

此外为了减小量化的损失，还需要在模型结构中插入伪量化节点，然后进行量化感知训练（QAT）。接着还需要将finetune后的模型存储为int8格式。然后还需要开发加载int8模型的推理加速库代码。最后就是本文讲到的整数矩阵乘法了。整个流程比较繁琐，这部分内容今后我会慢慢给大家分享。网上关于量化的优秀教程非常多，我不会讲太多理论上的量化知识，只会从实践的角度来白话一下我们在Transformer模型量化过程中做的一些尝试。

如果觉得有用，就请分享到朋友圈吧！

△点击卡片关注极市平台，获取最新CV干货

公众号后台回复“transformer”获取最新Transformer综述论文下载～