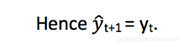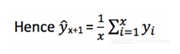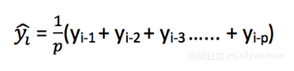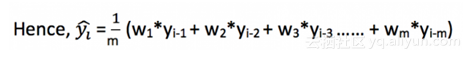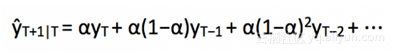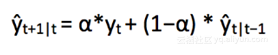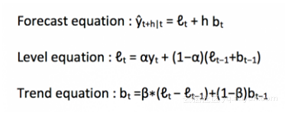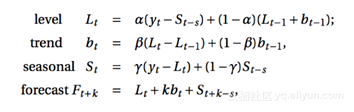(Python)时序预测的七种方法
云栖君导读:大多数人都听说过关于Cryptocurrency,许多人也许会投资他们的加密货币。但是,投资这种不稳定的货币安全吗?怎样才能确保现投资这些硬币未来一定能带来稳定的收益呢?我们不能确定,但肯定能根据以前的价格产生一个近似值。时序模型是预测的一种方法。
除了加密货币,还有许多重要的应用时序预测的领域,例如:销售预测,呼叫中心的通话量,太阳的活动,海潮,股市行为等等。
目录:
理解问题描述和数据集
安装库
方法 1 –以简单的方式开始
方法2 – 简单平均数
方法3 – 移动平均数
方法 4 –指数平滑法
方法5 – Holt线性趋势法
方法6 – Holt冬季季节法
方法7 –综合自回归移动平均法(ARIMA)
理解问题描述和数据集
提供了涉及预测JetRail通勤人数的时序问题,一个新的高速铁路服务。我们提供了2年的数据,并利用这些数据预测未来7个月的通勤人数。
在本文中,只使用训练数据集。
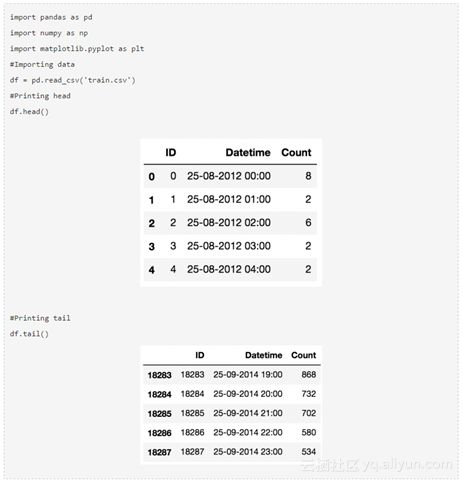
从以上的报表上看到,我们有2年的按小时计的通勤数据(2012-2014),需要预估未来的通勤数量。
在本文中,我构造子集和汇总数据集以便讲解不同的方法。
构造数据集的子集 (2012/08 – 2013/12)
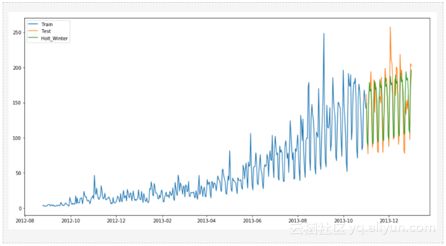
为建模构造训练和测试文件。前14个月的数据被用作训练数据(2012/08 - 2013/10),后两个月的被用作测试数据(2013/11 - 2013/12)。
每天汇总数据集。
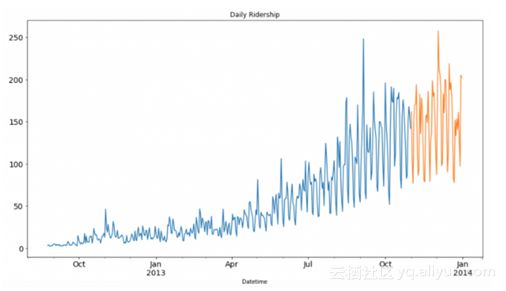
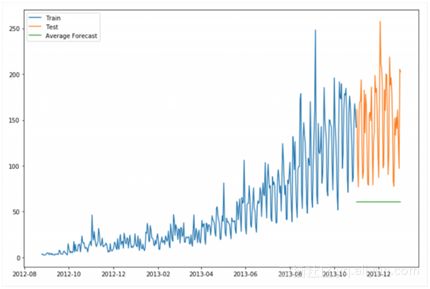
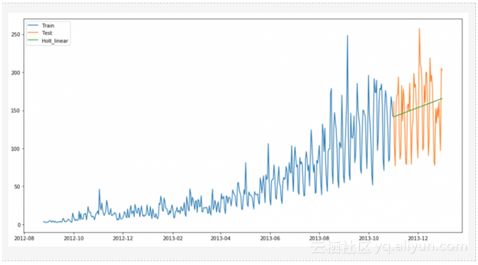
把数据(用于训练的和测试的)可视化,以了解在一段时间内是如何变化的。
安装库(statsmodels)
用来进行时序预测的库是statsmodels。在应用很少的给定方法之前,需要安装一下。statsmodels可能已经安装在你的Python开发环境了,但它不支持的预测方法。我们将从存储库克隆一下并进行源码安装。按照如下步骤 :
使用PIP冻结检查statsmodels是否已经安装在你的环境中;
如果已经存在,使用“conda remove statsmodels” 删除;
用 “git clone git://github.com/statsmodels/statsmodels.git”克隆statsmodels的存储库,在克隆前用“git init”初始化Git;
用“cd statsmodels”进入到statsmodels目录
用“python setup.py build”建安装文件;
用“python setup.py install”进行安装;
退出bash/terminal;
重启bash/terminal,打开python并执行“from statsmodels.tsa.api import ExponentialSmoothing”进行验证;
方法1: 用Naive方法开始
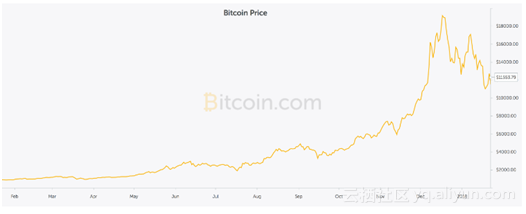
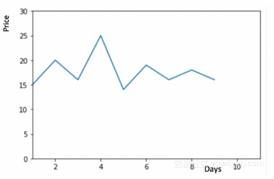
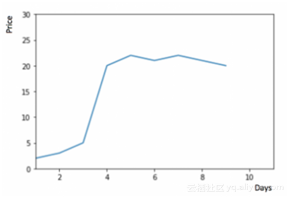
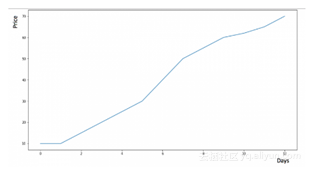
考虑下面的曲线图:
从图中我们可以看出,从一开始,硬币的价格是稳定的。大多时候我们都有一个在整个时间段都比较稳定的数据集。如果想预测第二天的价格,可以简单地用前一天的价格数据,估计第二天的价格。这种假定下一个期望点等于最后一个观测点的预测技术称为 Naive方法。
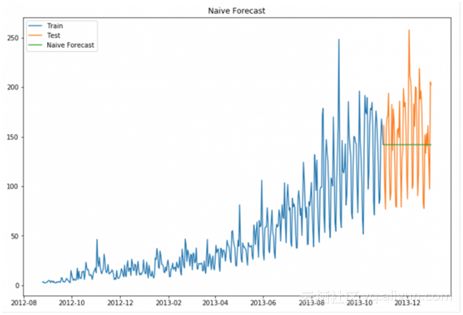
现在我们采用Naive 方法来预测测试数据的价格。
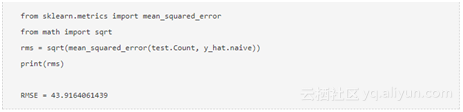
现在我们将计算均方根误差(RMSE)以检查测试数据集上模型的精度。
可以从RMSE值和上面的图推断,Naive方法不适合变化频繁的数据集,它最适合稳定的数据集。
方法2 简单均值法
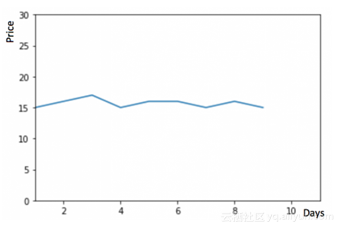
考虑下面的图。
可以从图中推断,硬币的价格是以微小的幅度随机上升和下降的,平均值不变。很多时候,我们得到了一个数据集,虽然它在整个时间段内有一个较小的变化,但是每个时间段的平均值保持不变。在这种情况下,我们可以预测第二天的价格与之前每天的平均值相近。
这种预测期望值等于所有观测点平均值的预测技术称为简单均值法。
我们取前面已知的所有值,计算平均值,并将其作为下一个值。当然,它并不精确,而是稍微接近。作为一种预测方法,实际情况是这个技术最有效。
现在将计算均方根误差检查模型的准确性
可以看出这种模式没有提高我们的分数。因此,我们能从得分推断,这种方法在每个时间段的平均值保持不变的时候效果最好。虽然Naive法的得分优于均值法,但这并不意味着Naive法在所有数据集上都优于均值法。
方法3 移动均值法
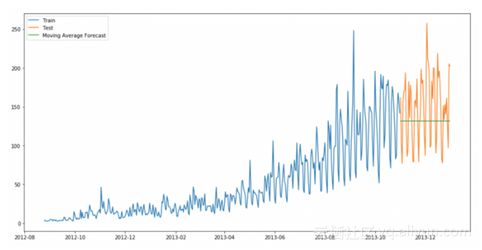
考虑下面曲线图,
从图中可以推断,硬币的价格在一段时间以前大幅度地提高了,但现在是稳定的。很多时候,我们得到了一个数据集,其中一段时间以前对象的价格/销售量急剧增加/急剧下降。使用初期的价格会对下一个时间段的预测产生很大影响。所以相对于简单均值法的改进,只计算最后几个时间段的平均价格。显然,只有最近的值才是重要的。这种利用时间窗计算平均值的预测技术称为移动均值法。
利用一个简单的移动均值模型,根据一个不变的有限数p的平均值来预测时间序列中的下一个或多个值。因此,对所有的 i > p。
移动均值法实际上是非常有效的,尤其是当你给序列选择正确的p值时。
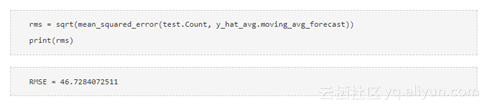
我们只选择了过去2个月的数据。现在将计算均方根误差来检查模型的准确性。
可以看到,Naive方法对于数据集要优于均值法和移动均值法。现在来看一下简单指数平滑法,看看它是如何执行的。
移动均值法的改进方法——加权移动均值法。在上述移动均值法中,我们同样权衡过去的N个观测值。但我们可能遇到的情况是,过去的每一次观察都以不同的方式影响预测。这种以不同的方式权衡过去观测值的技术称为加权移动均值技术。
加权移动均值是一个移动平均值,在滑动窗口的值中赋予不同的权重。
选择窗口的大小,需要一个权重列表。例如,如果选择[ 0.40,0.25,0.20,0.15 ]作为权重,将分别给出40%,25%,20%和15%。
方法4 简单指数平滑法
在理解了上述方法之后,可以注意到,简单均值法和加权移动均值法是完全相反的。我们需要在这两个方法之间采取某种方法,这两个方法在用不同的方式权衡数据点的同时要考虑所有数据。这种技术称为简单指数平滑法。预测是用加权平均来计算的,之前观测值的权重是指数递减的,最小的权重与最早的观测值相关:
0≤ α ≤1是参数。
先一步预测时间T + 1是一个序列中的所有观测值的加权平均值Y1,…,YT。权重下降的速率由参数α决定。
如果观察足够长的时间,你会看到,期望ŷx是α⋅YT和(1−α)⋅ŶT-1的和。
也可以写成 :
所以基本上我们已经有了一个1−α和α的加权移动平均值:。
可以看到,1−α乘以之前预期的表达递归的值ŷx−1。这就是为什么这种方法被称为Exponential。在时间t + 1的预测等于最近观察值yt 和最近预测值 ŷ t|t−1之间的加权平均值。
现在将计算均方根误差检查模型的准确性。
可以看到,用alpha值为0.6的简单指数模型形成一个更好的模型,到现在为止,生成一个更好的模型。
方法 5 霍尔特线性趋势法
我们现在已经学会了几种预测方法,但可以看到,这些模型在变化较大数据上不是太好。
趋势是在一段时间内观察到的价格的一般模式。如Naive方法会假定最后两点之间的趋势将保持不变,或者可以在所有点之间的平均斜率得到一个平均趋势,使用移动趋势均值或指数平滑法。
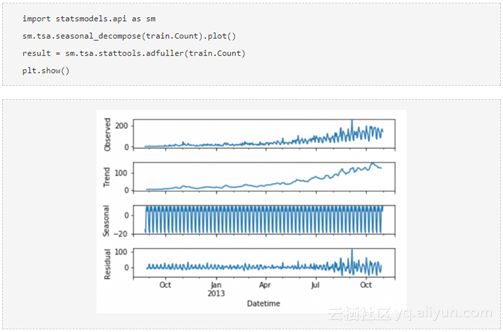
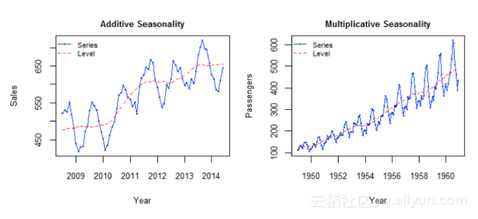
但我们需要一种方法,能准确无误地绘制趋势图。考虑数据集趋势的这种方法称为霍尔特线性趋势法。每个时间序列的数据集可以被分解为不同趋势的组成部分,季节性和剩余。任何跟随趋势的数据集都可以使用Holt线性趋势法进行预测。
从图表可以看出,该数据集呈增长趋势。因此,可以用Holt的线性趋势来预测未来的价格。
霍尔特扩展简单指数平滑方法,允许有趋势的数据预测。它只适用于两个等级(多个序列的平均值)和趋势的指数平滑方法。用数学符号表示,现在需要三个等式:一个用于等级,一个用于趋势,一个结合等级与得到预测值Ŷ的趋势
我们在上述算法中预测的值称为等级。在上面的三个等式中,可以注意到我们增加了等级和趋势来生成预测等式。
作为简单指数平滑法,这里的等级等式表明它是一个观察数的加权平均值和样本内前步预测。趋势等式表明,这是一个基于ℓ(t)−ℓ(t−1)和和b(t−1)的时间t的预测趋势的加权平均值。
我们将添加这些等式来生成预测等式。也可以通过乘以趋势和等级而不是增加,来生成乘法预测等式。当趋势呈线性上升或下降时,则采用加法等式,而当趋势呈指数下降时,则采用乘法等式。实践表明乘法是一种更稳定的预测,但加性方法更容易理解。
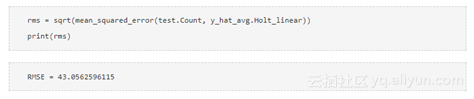
现在将计算均方根误差检查模型的准确性
方法6 Holt-Winters方法
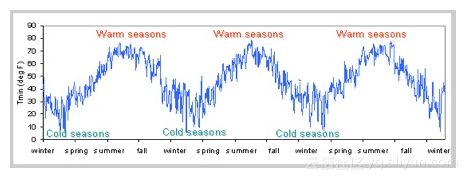
考虑一个位于山上的旅馆。在夏季期间有很高的访问量,而今年余下时间的游客相对较少。因此,业主的利润在夏季比其他季节都要好得多。而且每年都一样,是季节性的。数据集在一段固定的时间间隔内显示出相似性。
由于季节性因素,使用霍尔特冬季方法将是其它模型中最好的选择。霍尔特-温特斯季节性方法包括预测等式和三个平滑等式-一个似乎等级ℓt,一个是趋势bt,一个是季节组成部分 st,平滑参数α,β和γ。
其中S是季节性周期的长度,0≤α≤1, 0≤β≤1和0≤γ≤1。
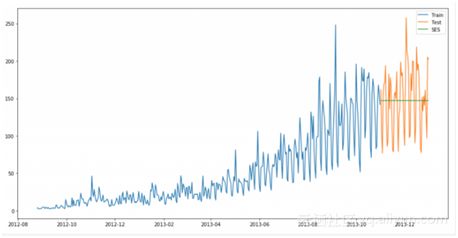
现在将计算均方根误差检查模型的准确性
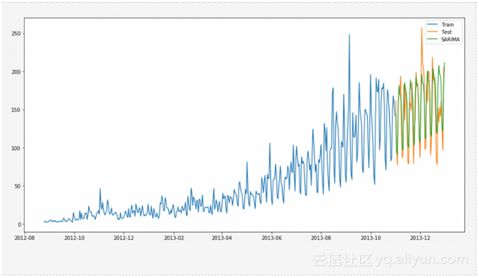
从图中可以看出,正确的趋势和季节性的映射提供了一个更好的解决方案。
方法7 ARIMA
另一个在数据科学家中非常流行的时间序列模型是ARIMA。它代表自回归积分移动平均(Autoregressive Integrated Moving average)。指数平滑模型是基于对趋势和季节性数据的描述,ARIMA模型的目的是描述数据之间的相关性。ARIMA的改进考虑到数据集的季节性,就像Holt-Winters方法一样。
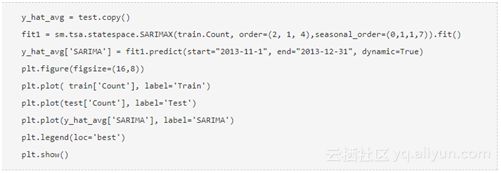
现在将计算均方根误差检查模型的准确性。
可以看到,使用季节性ARIMA生成一个类似Holt’s Winter的解决方案。我们选择的参数为ACF和PACF图。
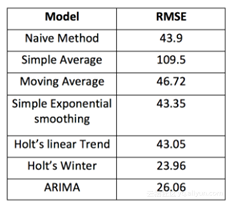
可以在MSE分数的基础上比较这些模型。
以上为译文。
本文由阿里云云栖社区组织翻译。
文章原标题《7 methods to perform Time Series forecasting (with Python codes)》,译者:Mags,审校:袁虎。
end
更多精彩