漫画:什么是归并排序?

————— 第二天 —————
————————————
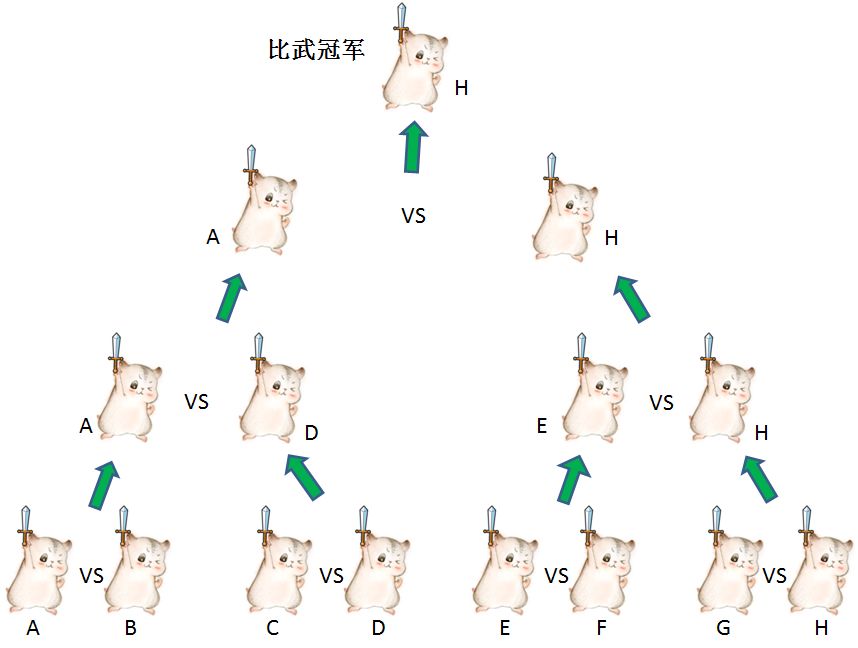
举个例子,有A、B、C、D、E、F、G、H一共8个武术家参考参加比武大会。
第一轮,两两一组,有4名选手胜出(四分之一决赛)
第二轮,两两一组,有两名选手胜出(半决赛)
第三轮,仅剩的两人一组,冠军胜出(总决赛)
归并排序和擂台赛,有什么相同和不同之处呢?让我们以下面这个数组来举例说明:
归并排序就像是组织一场元素之间的“比武大会”,这场比武大会分成两个阶段:
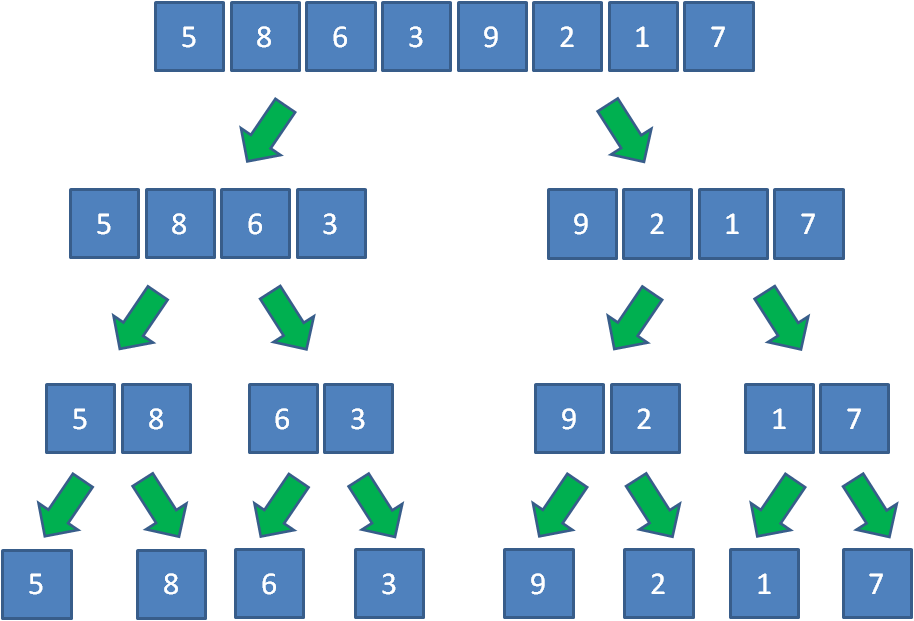
1.分组
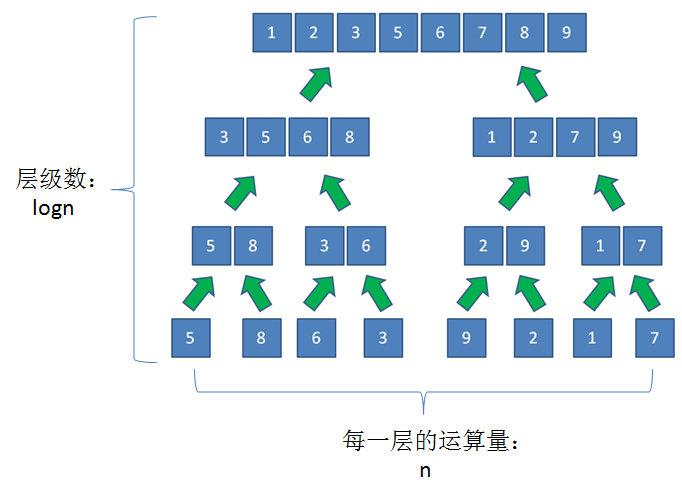
假设集合一共有n个元素,算法将会对集合进行逐层的折半分组。
第一层分成两个大组,每组n/2个元素;
第二层分成4个小组,每组n/4个元素;
第三层分成8个更小的组,每组n/8个元素;
......
一直到每组只有一个元素为止。
这样一来,整个数组就分成了一个个小小的“擂台”。
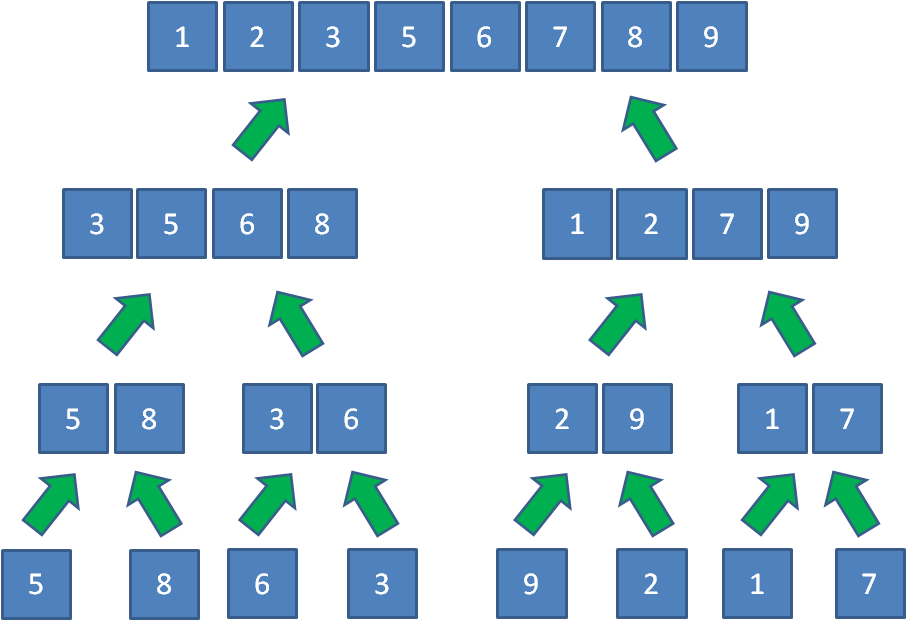
2.归并
既然分了组,接下来就要开始“比武”了。
归并排序和擂台赛有一个很大的不同,就是擂台赛只需要决定谁是老大,而并不关心谁做老二和老三;归并排序的要求复杂一些,需要确定每一个元素的排列位置。
因此,当每个小组内部比较出先后顺序以后,小组之间会展开进一步的比较和排序,合并成一个大组;大组之间继续比较和排序,再合并成更大的组......最终,所有元素合并成了一个有序的集合。
这个比较与合并的过程叫做归并,对应英文单词merge,这正是归并排序名字的由来。
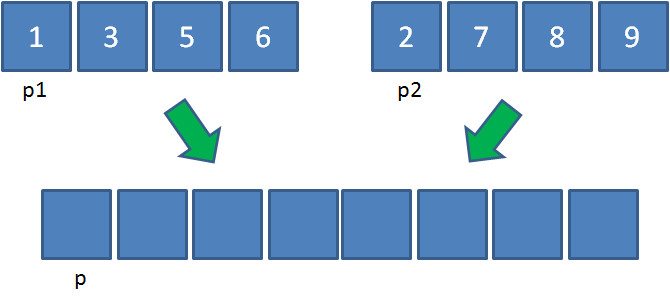
归并操作需要哪三个步骤呢?我们以两个长度为4的集合为例:
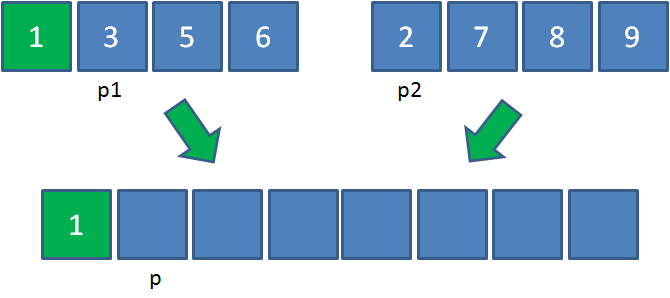
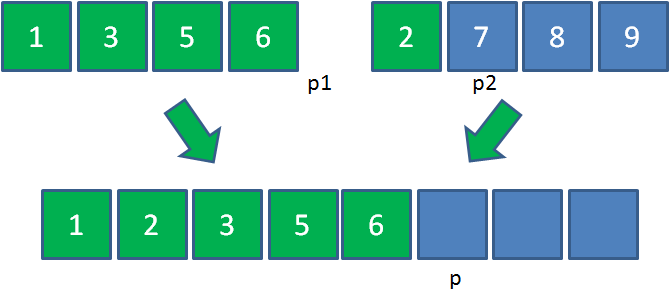
第一步,创建一个额外大集合用于存储归并结果,长度是两个小集合之和。(p1,p2,p是三个辅助指针,用于记录当前操作的位置)
第二步,从左到右逐一比较两个小集合中的元素,把较小的元素优先放入大集合。
由于1<2,所以把元素1放入大集合,p1和p各右移一位:
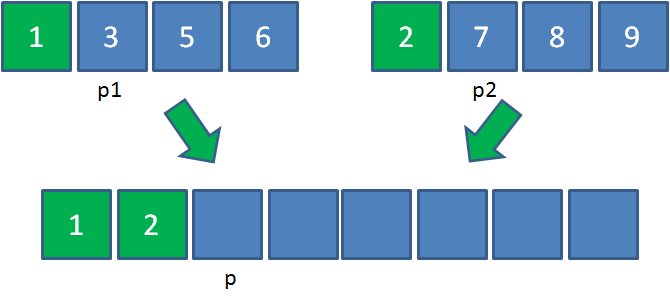
由于2<3,所以把元素2放入大集合,p2和p各右移一位:
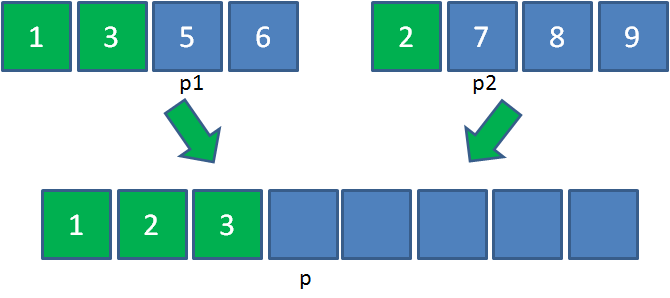
由于3<7,所以把元素3放入大集合,p1和p各右移一位:
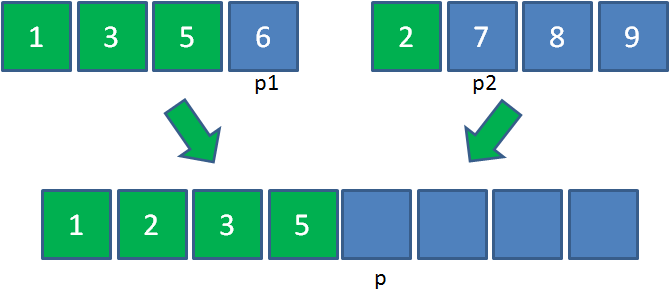
由于5<7,所以把元素5放入大集合,p1和p各右移一位:
由于6<7,所以把元素6放入大集合,p1和p各右移一位:
此时左侧的小集合已经没有元素可用了。
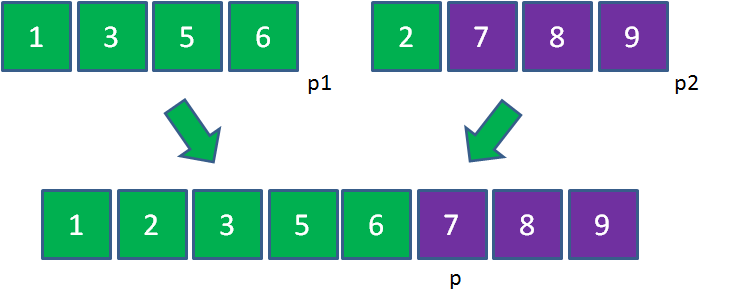
第三步,从另一个还有剩余元素的集合中,把剩余元素按顺序复制到大集合尾部。
这样一来,两个有序的小集合就归并成了一个有序的大集合。

static public void mergeSort(int[] array, int start, int end){
if(start < end){
//折半成两个小集合,分别进行递归
int mid=(start+end)/
2;
mergeSort(
array, start, mid);
mergeSort(
array, mid+
1, end);
//把两个有序小集合,归并成一个大集合
merge(
array, start, mid, end);
}
}
static private void merge(int[] array, int start, int mid, int end){
//开辟额外大集合,设置指针
int[] tempArray =
new
int[end-start+
1];
int p1=start, p2=mid+
1, p=
0;
//比较两个小集合的元素,依次放入大集合
while(p1<=mid && p2<=end){
if(
array[p1]<=
array[p2])
tempArray[p++]=
array[p1++];
else
tempArray[p++]=
array[p2++];
}
//左侧小集合还有剩余,依次放入大集合尾部
while(p1<=mid)
tempArray[p++]=
array[p1++];
//右侧小集合还有剩余,依次放入大集合尾部
while(p2<=end)
tempArray[p++]=
array[p2++];
//把大集合的元素复制回原数组
for (
int i=
0; i<tempArray.length; i++)
array[i+start]=tempArray[i];
}
public static void main(String[] args) {
int[]
array = {
5,
8,
6,
3,
9,
2,
1,
7 };
mergeSort(
array,
0,
array.length
-1);
System.out.println(Arrays.toString(
array));
}



☞“国家队”入局! 中移动、银联等宣布区块链服务网络(BSN)正式内测!
![]()
你点的每个“在看”,我都认真当成了喜欢