解读现代存储系统背后的经典算法

2018 年 7 月 10 日 AI前线

作者｜Alex Petrov

译者｜盖磊

编辑 | Debra

AI 前线导读：本文详细剖析了两种被大多数现代数据库使用的存储系统设计方法，即针对读操作优化的 B 树，以及针对写操作优化的 LSM 树，并介绍了两种方法的一些用例和权衡考虑。

更多干货内容请关注微信公众号“AI 前线”，（ID：ai-front）

文章最先发表在 ACM Queue 期刊第 16 卷第 2 期，可通过 ACM 数字图书馆查阅（https://portal.acm.org/citation.cfm?id=3220266）。引用该文章：“Alex Petrov. 2018. Algorithms Behind Modern Storage Systems. Queue 16, 2, pages 30 (April 2018), 21 pages. DOI: https://doi.org/10.1145/3212477.3220266.”。

应用处理的数据量在持续增长。数据的增长，对扩展存储能力提出了挑战。就此问题，每种数据库管理系统都有其自身的权衡考虑。对于数据管理者而言，理解这些权衡因素非常关键，这有助于从多种方式中做出正确的选择。

从读 / 写工作负载平衡、一致性需求、延迟和访问模式等方面看，应用是各异的。如果我们能对数据库和存储内部设施架构决策了然于胸，那么将有助于我们理解系统行为模式的原因所在，一旦在问题时能解决问题，并能根据工作负载调优数据库。

一个系统不可能在所有方面上都是最优的。确保无存储开销、提供最优读写性能的数据结构只存在于理想情况下，在实践中当然是不可能存在的。

本文详细剖析了两种被大多数现代数据库使用的存储系统设计方法，即针对读优化的 B 树1和针对写优化的 LSM（日志结构合并，log-structured merge）树 5，并分别给出了两种方法的一些用例和权衡考虑。

B 树

B 树是一种广为使用的读优化索引数据结构，是二叉树的一种泛化。它具有多种变体，并已用于多种数据库（包括 MySQL InnoDB4 和 PostgreSQL 7）和文件系统（例如，HFS+8、ext4 中的 HTrees 9）。B 树中的“B”表示“Bayer”，指的是数据结构的最初创立者 Rudolf Bayer，也可以说是 Bayer 彼时供职的波音公司（Boeing）。

二叉树中，每个节点有两个子节点（分别称为左子节点和右子节点）。保存在左子树和右子树中的键（Key），其值分别小于和大于当前节点的键。为维持树的深度最小，二叉树必须是平衡的。在添加随机顺序的键到树中时，最终很自然会导致树的一边比另一边更深。

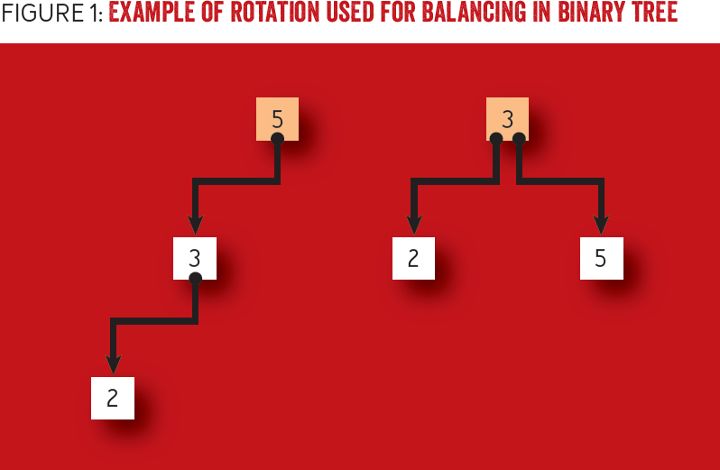
一种二叉树重平衡（rebalance）的法是称为“旋转”（rotation）方法。旋转方法实现节点的重新排列，它将更深子树的父节点下推到其子节点之下，并上移子节点为有效地置于父节点的原位置。图 1 给出了一个旋转方法的例子，实现了一个二叉树的平衡。左图的二叉树在添加了节点“2”之后，是不平衡的。为了平衡二叉树，我们以节点“3”为轴心旋转树，然后以节点“5”为轴线。节点“5”是原先的根节点，也是节点“3”的父节点，旋转后成为节点“3”的子节点。在完成旋转后得到右图的树，其中左子树深度降低了 1，右子树的深度增加了 1，而树的最大深度降低了。

图 1 例子：使用旋转方法平衡二叉树

二叉树是一种十分有用的内存数据结构。由于平衡（即需要保持所有子树的深度最小）和低扇出（每个节点最多具有两个指针）特性，二叉树在磁盘上的性能并不好。B 树允许每个节点存储两个以上的指针，并可将节点大小调整为适合页面的大小（例如，4KB），因此可在块设备上良好工作。当前，有一些实现中使用了更大规模的节点，甚至横跨多个页面。

B 数据有如下属性：

排序：排序支持顺序扫描，简化了查找。
自平衡：插入和删除操作无需重平衡树。一个 B 树节点在占满后，将分割（split）为两个节点。如果两个近邻节点的利用率（occupancy）降至某个阈值以下时，那么节点会合并（merge）。这意味着，各个叶子节点与根节点间是等距的，在查找时可以使用同样的步数定位。
查找操作有对数时间复杂度保证。这一点使 B 树成为数据库索引的很好选择，因为在数据库中，查找时间是非常关键的。
支持可变数据结构。插入、更新和删除（以及随后的节点分割和合并）是在磁盘上执行的，实现就地（in-depth）更新需要一定的空间开销。B 树可以组织为聚束索引，将实际数据存储在叶子节点上，也可以使用非聚束索引，将数据存储为堆文件。

本文还将介绍 B+ 树 3。B+ 树是 B 树的一种变体，常用于数据库存储。与原始 B 树相比，B+ 树的不同之处在于：1. B+ 树的叶子节点存储值并形成一个额外的链接层。2.B+ 树的内部节点并不存储值。

B 树剖析

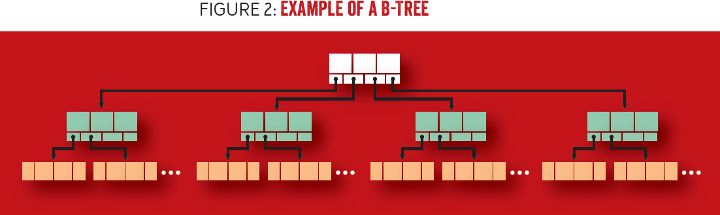
下面我们仔细查看 B 树的构建模块，如图 2 所示。B 树具有多种节点类型，包括根节点、内部节点和叶子节点。根节点（顶端）是没有父节点的节点（即它不是任何其它节点的子节点）。内部节点（中间）具有父节点和子节点，它们连接了根节点和叶子节点。叶子节点（底端）保存数据，它没有子节点。图 2 显示的 B 树的分支因子（branching factor）为 4，即具有四个指针，内部节点有三个键值，叶子节点有四个键值对。

图 2 例子：B 树

标识一个 B 树，可使用如下指标：

分支因子：即指向子节点的指针数（N）。考虑存在指针，根节点和内部节点最大可保存 N-1 个键值。
利用率：最大可用指针数中，当前有多少指向子项的指针在用。例如，如果树的分支因子是 N，节点当前保持了 N/2 个指针，那么利用率就是 50%。
高度：B 树的层数，指明了在查找中需遍历的指针个数。

树中每个非叶子节点最多保持 N 个键（索引项），将树分割为 N+1 个子树，这些子树可用相应的指针定位。在条目 Ki 中的指针 i 指向的子树中，所有索引项是 Ki-1 <= Ksearched < Ki（其中 k 是一组键）。第一个和最后一个指针是特例，最左子节点指向的子树中，所有的条目小于或等于 K0；最右子节点指向的子树中，所有的条目大于 KN-1。叶子节点中包含的指针，可指向同一层中前一个或后一个节点，形成近邻节点的双向链接列表。所有节点中，键总是排序的。

查找

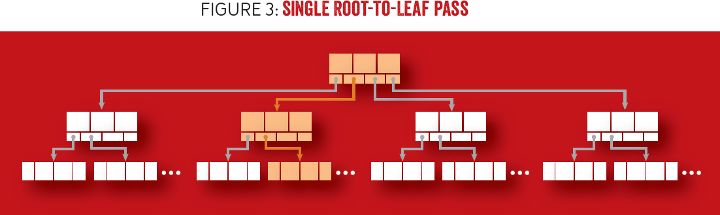
在执行查找时，搜索将从根节点开始，沿内部节点递归下行至叶子层级。在每一层级，通过追随子节点指针，搜索空间可缩减到子树范围（该子树包括搜索值）。图 3 显示的是 B 树中的一次查找，即一次沿着两个键间的指针由根到叶子的遍历，一个指针大于或等于搜索项，另一个指针小于搜索项。执行一个点查询（Point Query）时，搜索在定位到叶子节点后结束。在范围搜索中，会遍历所找到叶子节点的键和值，然后是近邻的叶子节点，直到到达范围的终点。

图 3 单次由根到叶子的遍历

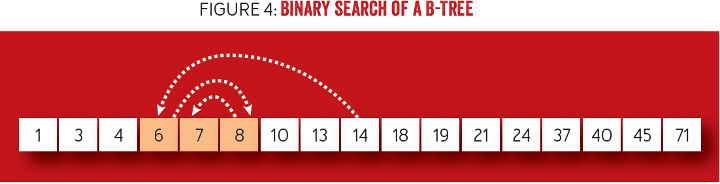
从复杂性上看，B 树保证了 log(n) 复杂度的查找，因为如何从节点中找到键中使用了二分查找法，如图 4 所示。二分查找法易于解释，当从字典中搜索具有某个首字母的单词时，所有单词是按字母顺序排列的。首先选择从确切的中间位置打开字典。如果搜索字母在字母序上要“小于”（先出现）打开的字母，那么继续在左半部份字典中搜索。否则，在词典右半部份中搜索。然后继续缩减剩余页面范围，通过减半并选择搜索方向，直到找到所需的字母。每步将搜索空间减半，使查找呈对数时间复杂度。B 树中的搜索具有对数时间复杂度，因为节点层级键是排序的，并在查找匹配总使用了二分查找。这也是为什么在整个树中保持高利用率和一致性是非常重要的。

图 4 B 树的二分查找

插入、更新和删除

执行插入时，第一步是定位目标叶子节点。在此可使用上面介绍的搜索算法。定位目标节点后，键和值将添加到该节点中。如果叶子节点的空间不够用，这种情况称为“溢出”（Overflow），叶子节点必须分割为两个。分割的实现是通过分配一个新叶子，将原叶子节点中的半数元素移动到新的叶子节点，并在父节点中分配一个指向新叶子节点的指针。如果父节点中也没有空余的空间，那么就在父节点层级执行分割操作。操作将持续直至到达根节点。如果根节点溢出，节点内容在新分配节点间分割。然后根节点自身将被覆盖，以避免重新分配。这也意味着，树（及树的高度）的高度总是在分割根节点时增长。

LSM 树

日志结构合并（LSM）树是一种写优化的数据结构，它是不可变的、驻留于磁盘的，适用于写操作比查找和检索记录更为频繁的系统。由于 LSM 树消除了随机插入、更新和删除，因此它得到了更多的关注。

LSM 树剖析

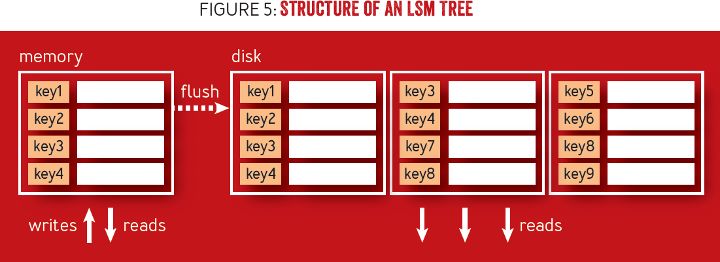
为支持顺序写，LSM 树在一个驻留内存表（通常使用支持对数时间复杂度查找的数据结构实现，例如二分查找树或跳表）中批量写入和更新，直至内存表规模达到一个设定的阈值，这时再写入到磁盘，该操作称为“刷新”（flush）。检索数据需要搜索树驻留磁盘的所有部分，检查驻留内存表，并在返回结果前合并内容。图 5 显示了一个 LSM 树的结构，其中的驻留内存表用于写入。一旦内存表达到了一定规模大，其中经排序的内容就要就写入到磁盘。读取时需要访问驻留磁盘和驻留内存表，并需要一个合并过程去整合数据。

图 5 LSM 树的结构

排序字符串表（SSTable）

现代多种系统中，例如 RocksDB 和 Apache Cassandra，将 LSM 树的驻留磁盘表实现为一种 SSTable（排序字符串表）。SSTable 具有简单性（易于写入、搜索和读取）及合并属性（在合并期间，源 SSTable 扫描和合并结果写是顺序操作）。

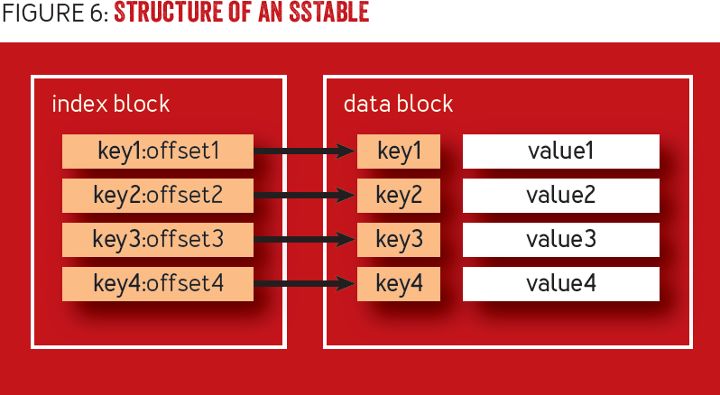
SSTable 是一种不可变的、驻留磁盘的排序数据结构。如图 6 所示，SSTable 在结构上可分为两个部分，即数据块和索引块。数据块是由顺序写入的唯一键值对组成，键值对按键排序。索引块中的键包含映射到数据块指针，指针指向实际记录的位置。索引通常实现为针对快速搜索优化的格式，例如 B 树，或是对于点查询使用哈希表。SSTable 中的每个值项具有一个与之相关联的时间戳。时间戳指定了插入和更新的写入时间（通常不做区分），以及删除的移除时间。

图 6 SSTable 的结构

SSTable 具有一些很好的特性：

点查询（即根据键找到一个值）可通过查找主索引快速完成。
扫描（即在指定键范围内迭代所有键值对）可以高效完成，仅通过在数据块内顺序读取键值对。

SSTable 给出了一段时间内所有数据库操作的快照。因为 SSTable 是由驻留内存表的刷新操作创建的，该表作为此时期内对数据库状态操作的一个缓冲区。

查找

检索数据时，需要搜索磁盘上所有的 SSTable，检查驻留内存表，并在返回结果前合并其中的内容。读操作需要合并过程，因为所搜索的数据可能存在于多个 SSTable 中。

为确保实现删除和更新，也必须要合并步骤。删除时，会在 LSM 树中插入一个占位符，通常称为“墓碑”（tombstone）。墓碑用于标记被删除的键。类似地，更新时也仅是增加一个具有更迟时间戳的记录。在读取期间，将跳过被标记为删除的记录，不返回给客户。更新中也采取类似的做法，对于两个具有同一键的记录，只返回时间戳更晚的记录。图 7 显示了合并是如何整合存储在独立表中具有同一键的数据。如图所示，Alex 的记录写入的时间戳为 100，更新了电话后记录的时间戳为 200。John 的记录是被删除的。其它两个条目保持原状，因为它们并未做标记。

图 7 例子：合并步骤

为减少需搜索的 SSTable 数量，避免因为搜索某个键而检查每个 SSTable，一些存储系统使用了一种称为布隆滤波器 10 的数据结构。布隆滤波器是一种概率数据结构，可用于检测一个元素是否属于一个集合的成员。它会产生误报匹配（即指出元素是集合的成员，但是事实上并不是），但是不会产生漏报（即如果返回结果是不匹配，那么该元素一定不是集合的成员）。换句话说，布隆滤波器可用于告知一个键是否“可能位于 SSTable 中”，或是“绝对不在 SSTable 中”。如果一个 SSTable 被布隆滤波器返回为不匹配，那么将在查询中跳过。

维护 LSM 树

鉴于 SSTable 是不可变的、是顺序写的，并且并未保留就地更改的空间。这意味着，插入、更新和删除操作需要重写整个文件。所有修改数据库状态的操作，是在内存驻留表中“批量处理”的。随时间的推进，驻留磁盘表的数量将会增长（对应同一键的数据可能会位于多个文件、同一记录的多个版本，或标记为删除的冗余记录中），读取将继续变得代价更为昂贵。

为降低读取的代价、整合被标记的记录空间并降低驻留磁盘表的数量，LSM 树需要一个紧缩（compaction）过程。紧缩过程从磁盘读取整个 SSTable，并合并它们。因为 SSTable 是按键排序的，紧缩过程的工作方式类似于归并排序，所以该操作也是非常高效。记录从多个数据源顺序读取，合并的输出可以即刻顺序地附加到结果文件中。归并排序的一个优点是工作高效，即便是对于归并无法放入内存中的大型文件。生成的表将保持原始 SSTable 的排序。

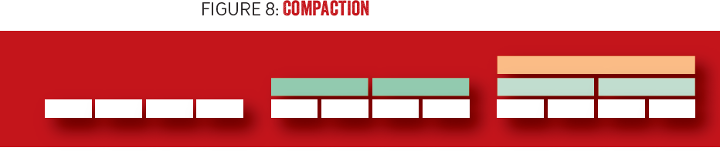
在紧缩过程中，合并后的 SSTable 将被抛弃，并被更“紧缩”的表替代，如图 8 所示。紧缩操作输入为多个 SSTable，输出为合并后的一个表。一些数据库系统在逻辑上将同一规模的表分组为同一“层级”，并在某个层级中的表数量足够多时，开始合并过程。紧缩减少了必须要处理的 SSTable 数量，使查询更加高效。

图 8 紧缩过程

原子性和持久性

为实现 I/O 操作数量减少和顺序化，B 树和 LSM 树均在更新实际发生前做内存中的批处理。这意味着，一旦发生失败，不能保证数据的完整性，而且也不能确保原子性（指一组更改的应用是原子化的，如同单个操作一样，或者全部应用，或者全不应用）和持久性（确保在进程崩溃或掉电时，数据处于一致性存储中）。

为解决这个问题，很多现代存储系统使用了 WAL 技术（预写式日志，Write-Ahead Logging）。WAL 的主要理念是所有数据库状态修改首先持久保持在位于磁盘上的只添加日志中。一旦操作过程中发生进程崩溃，就会重执行日志，以确保没有数据丢失，实现所有更改的原子化。

B 树中，使用 WAL 可理解为更改只有做日志后，才写到数据文件中。通常情况下，B 树存储系统的日志规模相对较小。一旦更改应用到持久存储，就会被丢弃。WAL 作为一种对未日志化（in-flight）操作的备份机制，即应用到数据页面的任何更改都可以从日志记录重做。

LSM 树中，WAL 用于持久化那些操作了内存表但是并未完全刷新到磁盘的更改。一旦内存表完全刷新并切换，读取操作可以在新创建的 SSTable 上完成，就可以丢弃保持了刷新内存表数据的 WAL 段。

总结

B 树和 LSM 树结构上的最大差别之一，在于优化的目的，以及优化的意义。

下面对 B 树和 LSM 树做一个对比。总而言之，B 树具有如下属性：

B 树是可变的，这支持通过引入一些空间开销，以及更为关联的写路径，实现就地更新。B 树并不需要完全的文件重写或多源合并。
B 树是读优化的。即 B 树不需要从多个源读取（因此也不需要此后的合并操作），这简化了读路径。
写可能会触发节点的级联分割，这会使一些写操作更昂贵。
B 树是针对分页（块存储）环境优化的，其中不存在字节地址。They are optimized for paged environments (block storage), where byte addressing is not possible.
虽然也需要重写，但是通常情况下 B 树存储要比 LSM 树存储需要更少的维护。
并发访问需要读 / 写隔离，其中一系列的锁和闩（latch）。

LSM 树具有如下特性：

LSM 树是不可写的。SSTable 是一次性写入磁盘的，永不更新。紧缩操作通过从多个数据文件移除条目，并合并具有相同键的数据，实现空间的整合。在紧缩过程中，已合并的 SSTable 将被丢弃，并在成功合并后移除。不可写提供的另一个有用特性，就是刷新后的表可并发访问。
LSM 是写优化的。这意味着写入操作将被缓存，并顺序地刷新到磁盘中，潜在地支持磁盘上的空间本地性。
读操作可能需要从多个数据源访问数据。因为不同时间写入的具有相同键的数据，可能会落在不同的数据文件中。记录在返回给客户前，必须经过合并过程。
LSM 树需要做维护和紧缩，因为缓存的写入操作将被刷新到磁盘。

存储系统的评估

在存储系统的开发中，总是需要考虑一些挑战和因素。优化目标对存储系统选择有着切实的影响。如果可以在写操作上花费更多时间，那么就可以部署针对更高效读操作的结构，预留额外的空间用于就地更新。这有利于实现更快的写操作，并支持将数据缓存在内存中，以确保顺序的写操作。但是，所有这些是不可能一次性达成的。我们理想中的存储系统具有最低的读代价、最低的写代价，并没有其它开销。但在实践中，数据结构需折衷考虑多个因素。理解这些折衷考虑是非常重要的。

哈佛大学 DASlab（数据系统实验室）的研究人员总结了数据库系统优化的三个关键参数：读开销、更新开销和内存开销，统称为“RUM”。对于特定的用例，理解这些参数中哪个是最重要的，将对数据结构、访问方法，甚至是特定工作负载的适用性产生影响，因为算法需要根据特定的用例做出调整。

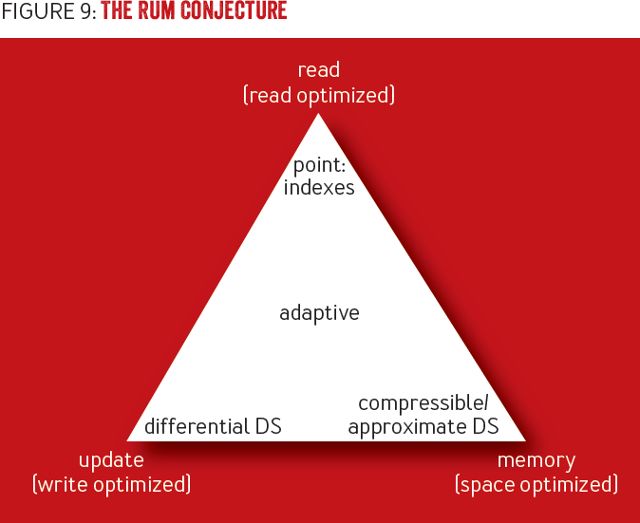
“RUM 假说”（http://daslab.seas.harvard.edu/rum-conjecture/）2 指出，如果对 RUM 中的两项设置上限，那么也会对第三项设置下限。例如，B 树是读优化的，代价是写开销，以及预留了额外的空间（因而导致了内存开销）。LSM 树空间开销更少，代价是在读操作期间必须访问多个驻留磁盘表，从而引入了读开销。这三个参数形成了一个完全三角形，改进其中的一项，意味着对其它项的折衷考虑。图 9 展示了 RUM 假说。

图 9 RUM 假说

B 树是针对读性能优化的。索引的布局方式使得遍历树所需的磁盘访问次数最小化。定位数据时，只需访问单个索引文件。这是通过保持索引文件可写而实现的。可写增加了写入放大（Write Amplification）问题，该问题由节点分割、合并、重定位和碎片化 / 不平衡相关维护等导致。为缓解更新的代价，并降低分割的次数，B 树在各个层级的节点中预留了额外的空闲空间。这有助于推迟发生写入放大问题，直至节点空间满。简而言之，B 树是在更新和内存开销间做了权衡，目的是实现更好的读性能。

LSM 树针对写性能优化。无论更新或是删除，都需要定位数据在磁盘上的位置（B 树也需要）。LSM 树通过在内存驻留表缓存所有插入、更新和删除操作以保证顺序写。这样做的代价是更高的维护代价、需要紧缩操作（紧缩操作只是一种缓解不断增长的读代价、减少驻留磁盘表数量的方式），以及更昂贵的读（因为数据必须从多个源读取并合并）。同时，LSM 树不保持任何空闲空间，这消除了一些内存开销（不同于 B 树节点平均利用率为 70%，就地更新需要一定的开销）。由于 LSM 树最终文件是不写的，为实现更好的使用率，需要支持块压缩。简而言之，LSM 树是在读性能和维护更好写性能和低内存开销间的权衡。

对于每种所需的特性，都会存在针对此特性优化的数据结构。如果使用相适应的数据结构以支持更好的读性能，那么代价是更高的维护代价。添加元数据有利于遍历（例如分散层叠（fractional cascading）），这将影响写的时间，并占用空间，但是可以改进读的时间。使用压缩技术 (例如，Gorilla 压缩 6、delta encoding 等算法) 可优化内存效率，将对写时数据打包和读时数据解包添加一些开销。有时，我们可以权衡功能和效率。例如，堆文件和哈希索引由于文件格式的简单性，可以给出很好的性能保证，以及更小的空间开销，但代价是只能支持执行点查询。我们还也可以通过使用近似数据结构，例如布隆滤波器、HyperLogLog、Count-Min sketch 等，权衡空间精度和效率。

读、更新和内存这三种可调整的开销，有助于我们评估数据库，并更深入理解数据库适合何种工作负载。三者非常直观，很容易将存储系统排序在一个桶中，给出执行情况的猜测，进而通过深入的测试去验证这一假设。

当然，评估存储系统时还存在其它一些重要的因素，例如维护代价、操作简单性、系统需求、对频繁更新和删除的适用性、访问模式等。RUM 假说仅是有助于给出直观感觉，并对最初方向提供经验法则。理解我们自己的工作负载，这是迈向构建可扩展的后端系统的第一步。

在不同的实现中，一些因素可能会发生变化。即便是使用类似存储设计原则的两个数据库间，最终的表现也可能会完全不同。数据库是一个复杂的系统，其中有很多变动因素。数据库也是很多应用中重要且不可分割的部分。性能上的权衡有助于我们一窥数据库的底层机制。了解底层数据结构及内部原理间的差异，有助于我们从中做出最优的选择。

参考文献

Comer, D. 1979. The ubiquitous B-tree. Computing Surveys 11(2); 121-137;

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.96.6637.

哈佛大学 DASlab 实验室. The RUM Conjecture;

http://daslab.seas.harvard.edu/rum-conjecture/.

Graefe, G. 2011. Modern B-tree techniques. Foundations and Trends in Databases 3(4): 203-402;

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.219.7269&rep=rep1&type=pdf.

MySQL 5.7 参考手册. InnoDB 索引的物理结构 ;

https://dev.mysql.com/doc/refman/5.7/en/innodb-physical-structure.html.

O'Neil, P., Cheng, E., Gawlick, D., O'Neil, E. 1996. The log-structured merge-tree. Acta Informatica 33(4): 351-385;

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.44.2782.

Pelkonen, T., Franklin, S., Teller, J., Cavallaro, P., Huang, Q., Meza, J., Veeraraghavan, K. 2015. Gorilla: a fast, scalable, in-memory time series database. Proceedings of the VLDB Endowment 8(12): 1816-1827;

http://www.vldb.org/pvldb/vol8/p1816-teller.pdf.

Suzuki, H. 2015-2018. The internals of PostgreSQL;

http://www.interdb.jp/pg/pgsql01.html.

Apple HFS Plus Volume 格式 ;

https://developer.apple.com/legacy/library/technotes/tn/tn1150.html#BTrees

Mathur, A., Cao, M., Bhattacharya, S., Dilger, A., Tomas, A., Vivier, L. (2007). The new ext4 filesystem: current status and future plans. Proceedings of the Linux Symposium. Ottawa, Canada: Red Hat.

Bloom, B. H. (1970), Space/time trade-offs in hash coding with allowable errors, Communications of the ACM, 13 (7): 422-426

HP 实验室 Goetz Graefe 的文章“五分钟规则（https://queue.acm.org/detail.cfm?id=1413264）：20 年后闪存将如何改变规则”。旧规则将持续演进，同时闪存给出了两个新规则。

https://queue.acm.org/detail.cfm?id=1413264

Rick Richardson，“数据库消岐”（https://queue.acm.org/detail.cfm?id=2696453）。使用针对用户访问模式构建的数据库。

https://queue.acm.org/detail.cfm?id=2696453

Poul-Henning Kamp，“这样做并不正确”（https://queue.acm.org/detail.cfm?id=1814327）。你是否认为自己已经掌握了如何处理服务器性能问题？再考虑一下。

https://queue.acm.org/detail.cfm?id=1814327

作者简介

Alex Petrov（http://coffeenco.de/，@ifesdjeen (GitHub)， @ifesdjeen (Twitter)）是 Apache Cassandra 项目的提交者，也是存储系统技术爱好者。他在多家企业从事数据库、构建分布式系统和数据处理流水线方面的工作。

查看英文原文：

https://queue.acm.org/detail.cfm?id=3220266