如何评估AI在医学影像识别中的应用效果？

作者 | 魏奇杰，丁大勇，李锡荣

编辑 | Natalie

AI 前线导读： 基于人工智能（AI）技术的医学影像识别越来越受到社会各界的重视。而人工智能技术的进步，往往被归纳为几个性能指标，这样一来，AI 技术的性能指标自然也就成为大家谈论和关注的焦点之一。实践中存在多种衡量 AI 算法性能的指标，本文尝试解释其中常见的几种指标的含义，以及它们在不同场景下的适用性和局限性，希望能够帮助大家更好地理解指标背后 AI 技术的进展。

更多优质内容请关注微信公众号“AI 前线”（ID：ai-front）

医疗影像识别中有哪些常用指标？

为简化讨论，本文均以“二分类问题”为例，即对影像判断的结果只有两种：要么是阳性（positive），要么是阴性（negative）。这样的简化也符合大部分医学影像识别问题的实际情况。

二分类问题，如果不能被 AI 模型完美解决，那么模型预测结果的错误大概有两类：一类是把阴性误报为阳性（把没病说成了有病），另一类是把该报告的阳性漏掉（即把有病看成了没病）。优化模型的过程，是同时减少这两类错误的过程，至少是在两类错误之间进行适当折中的过程。不顾一类错误，而单纯减少另一类错误，一般是没有意义的。比如，我们为了不犯“漏”的错误，最简单的办法就是把所有的图像都报告称阳性（有病）。

1. 常用术语解释

在二分类的条件下，AI 的预测结果存在下列 4 种情形：

• 真阳性（True Positive，TP）：预测为阳性，实际为阳性；

• 真阴性（True Negative，TN）：预测为阴性，实际为阴性；

• 假阳性（False Positive，FP）：预测为阳性，实际为阴性；

• 假阴性（False Negative，FN）：预测为阴性，实际为阳性。

其中，FP 也称为误报（False alarm），FN 也称为漏报（miss detection）。

上文 4 种名称中的“真”（True）和“假”（False）表示预测结果是否正确。名称中的“阳性”（Positive）和“阴性”（Negative）表示预测结果。例如，对于一个特定的测试样本，真阳性的含义为“AI 预测正确，且 AI 预测结果为阳性”，那么就可以推断到：预测为阳性，实际结果为阳性。假阴性的含义为“AI 错判为阴性”，那么就可以推断到：预测为阴性，实际结果为阳性。

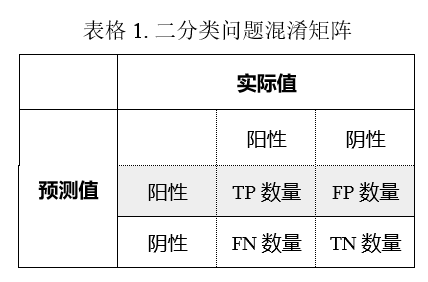
通常我们会用一个矩阵来展示预测结果和实际情况的差异，称为混淆矩阵 (confusion matrix)。二分类的混淆矩阵为 2x2 的，见表 1。为表述方便起见，接下来我们就以 TP 代指真阳性的数量，TN 代指真阴性的数量，FP 代指假阳性的数量，FN 代指假阴性的数量。

2. 可以由混淆矩阵得到的指标

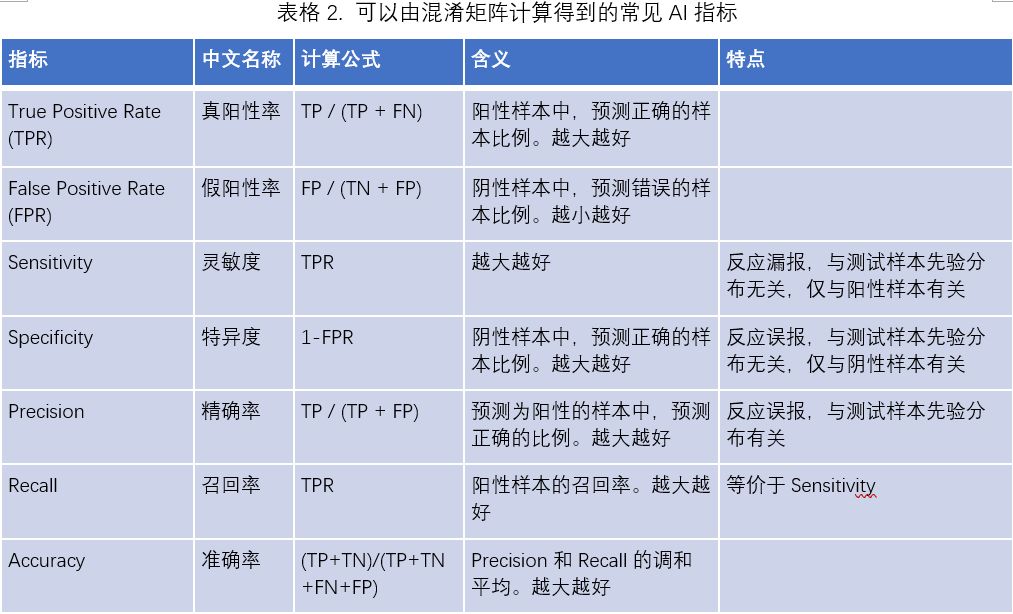
表 2 中列出了常用的可以由混淆矩阵得到的衡量指标，即这些指标都能直接由 TP、TN、FP、FN 四个值表示出来。

表 2 中涉及到的指标，取值范围均是 0 至 1。由于上述两类错误的存在，通常这些指标需要成对地报告，成对地去考察。

例如，如果我们只关心 AI 模型的灵敏度（Sensitivity），那么我们就只需要把所有的样本预测为阳性，那么 Sensitivity 就等于 1。显然，这不是一个好的模型，因为它会将阴性样本误报为阳性，使得它的特异度（Specificity）为 0。因此，需要同时报告 Sensitivity 和 Specificity。

精确率（Precision）和召回率（Recall）、真阳性率（TPR）和假阳性率（FPR）也存在类似的此消彼长的关系，我们不再对这些指标单独讨论。准确率（Accuracy）通常也会和其它指标一起报告，我们会在下文各指标使用场景具体讲到。

当同时报告两个指标（例如 Sensitivity 和 Specificity）时，我们通常还会报告二者的“平均值”，使得模型的指标归为一个点，以便比较两个模型的好坏。这里我们通常使用二者的调和平均数，称为 F1-measure。选调和平均数的原因是调和平均数相比于算数平均数和几何平均数，更加偏向小的那个数。给定两个指标，它们的各种平均数之间存在如下关系：

调和平均数 ≤ 几何平均数 ≤ 算数平均数

当且仅当两个指标相等时，上述等式成立。这就要求我们找到这样一个模型，使得两个指标尽量均衡。

3. 不能由混淆矩阵得到的指标

一个 AI 模型通常不是直接得到阳性或者阴性的结果的。它输出的是阳性（或者阴性）的得分（也可被称为阳性的“概率”或者“置信度”，尽管它实际上和概率或者置信度并无关系）。通常是得分越大，表明模型越肯定这是一个阳性病例。为了把得分转化为阳性 - 阴性的二分类，我们会认为设置一个决策阈值（decision threshold）。当模型关于某个样本的阳性得分大于该阈值时，该样本被预测为阳性，反之则为阴性。

例如，当阈值设为 0.5 时，模型输出的样本 1 的得分为 0.7，则样本 1 被预测为阳性。模型输出的样本 2 的得分为 0.1，则样本 2 会被预测为阴性。上述二分类的过程实质上就是将模型给出的连续得分量化为阳性、阴性这两个离散值之一。阈值一旦确定，就可以计算相应的混淆矩阵。

因此，上一节讲到的所有指标，都是可能随着阈值变动而改变的。例如，将阈值由 0.5 提高到 0.6 时，预测为阳性的样本有很大可能会减少，由此导致误报减少而漏报增多，相应的指标也随之变动，具体表现为 Sensitivity 下降而 Specificity 提升。

为方便起见，我们假设所有的得分均在 0 和 1 之间。

(1)ROC 曲线和 AUC

随着阈值的降低，预测的阳性病例增加，预测的阴性病例减少，即 TPR 上升，FPR 上升，以 TPR 为纵坐标，FPR 为横坐标画出 ROC 曲线，如图 1 所示。可以看出，ROC 曲线是 TPR 关于 FPR 的不减函数。

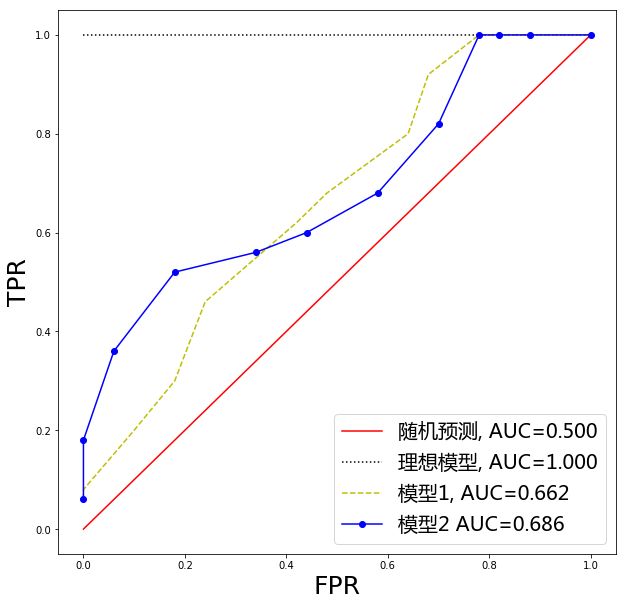
图 1. ROC 曲线

回顾表 1，可知 TPR 就是 Sensitivity，而 FPR 等于 1-Specificity。因此，也可以认为 ROC 曲线的横坐标是 1-Specificity，纵坐标是 Sensitivity。

ROC 曲线起始点对应的阈值为 1，即将所有样本均预测为阴性，此时阳性样本全被误报为阴性（TP=0），而阴性样本没有被误报（FP=0），因此有 TPR=FPR=0。ROC 曲线终点对应的阈值为 0，即所有样本均预测为阳性，此时 TPR=FPR=1。

当模型 1 的 ROC 曲线被算法 2 的 ROC 曲线严格包围时，意味着在相同的 FPR（或 Specificity）要求下，模型 2 的 TPR（或 Sensitivity）更高，可以认为模型 2 优于模型 1，如图 1 中的模型 1 就优于随机预测。

当不存在某条 ROC 曲线被另一条完全包围时，如图 1 中模型 1 和模型 2 的所示，我们通常使用 ROC 曲线下的面积作为度量指标，称之为 AUC。

(2)Precision-Recall 曲线（P-R 曲线）和 Average Precision（AP）

除了 ROC 曲线，另一种常用的是 Precision-Recall 曲线，简称 P-R 曲线。随着阈值的降低，预测的阳性病例增加，预测的阴性病例减少。模型将更多的它认为“不那么确定是阳性” 的样本判断为阳性，通常 Precision 会降低。并且 Recall 不减。以 Precision 为纵坐标，Recall 为横坐标画出 P-R 曲线，如图 2。

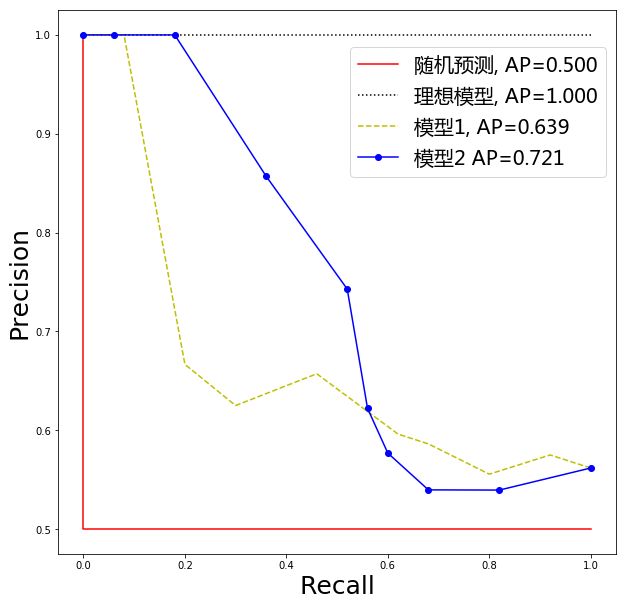
图 2. P-R 曲线

P-R 曲线起点对应的阈值为所有预测样本得分的最大值，即只将模型认为最有可能是阳性的那一个测试样本预测为阳性，其余全预测为阴性，如果这一个阳性预测正确，那么 Precision=1，Recall=1/ 所有阳性病例数，否则 Precision=Recall=0。P-R 曲线终点对应的阈值是 0，即将所有样本预测为阳性，此时 Precision= 所有阳性病例数 / 总病例数，Recall=1。同样我们使用 P-R 曲线下的面积作为度量指标，称为 AP。

AP 和 AUC 与具体的阈值无关，可以认为是对模型性能的一个总体估计，因此通常作为更普适的指标来衡量模型的好坏。

不同指标在实际场景下的应用

我们用一个简单的图来帮助理解，如图 3，红色代表阳性，绿色代表阴性，小人头的颜色代表实际类别，手中拿的诊断颜色代表模型预测的类别。

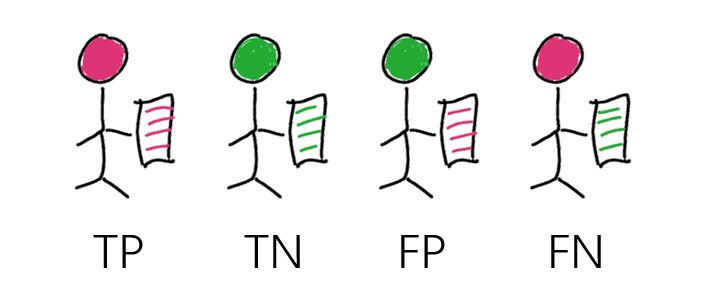
图 3

1. 理想的 AI 模型

所有的阳性都被预测为阳性，所有的阴性都被预测为阴性。如图 4。

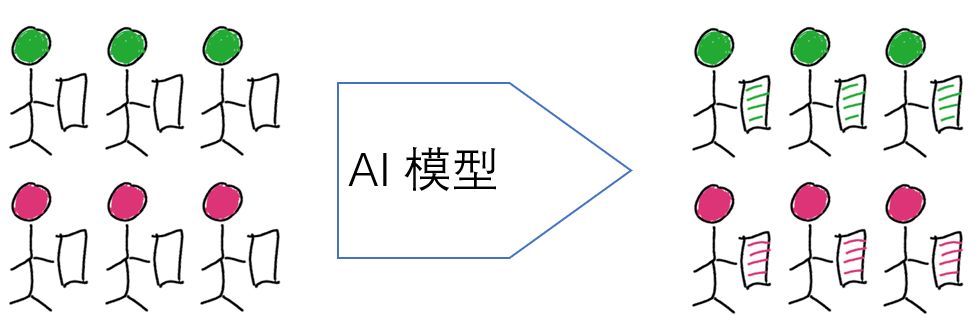
图 4

在这种情形下，Sensitive=Specificity=Precision=Recall=1。

2. 实际的 AI 模型

图5

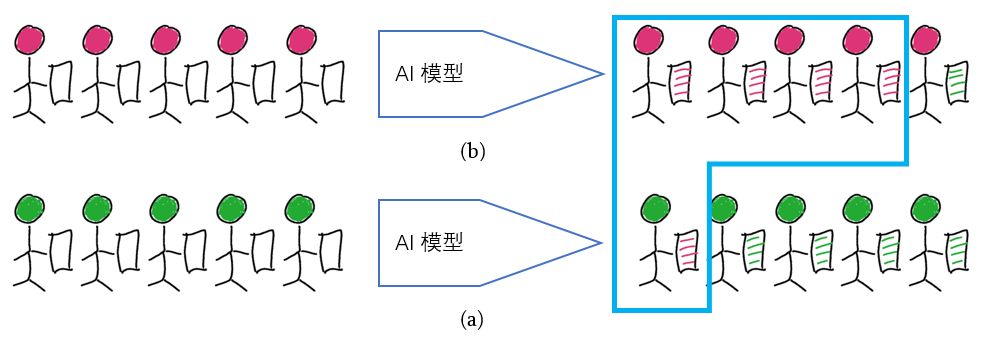
实际中，模型不可能做到完全正确。第一种情况，如图 5。图 5（a）中 5 个阳性中有 4 个被正确预测为阳性，Sensitive=4/5=0.8。图 5（b）中 5 个阴性中有 4 个被正确预测为阴性， Specificity=4/5=0.8。一共 5 个病例被预测为阳性（蓝框），其中 4 个正确，Precision=4/5=0.8。

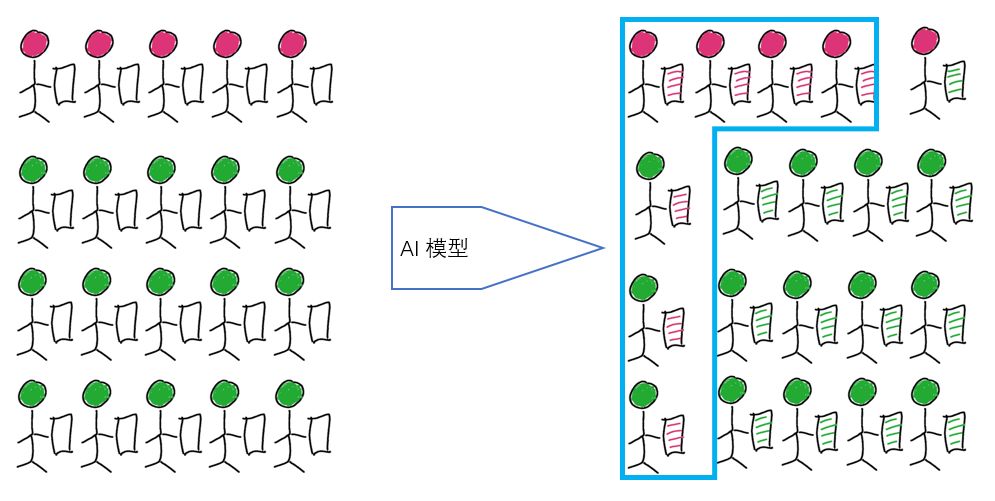
第二种情况，如图 6 所示，相对于第一种情况，我们将阴性的样本量增加两倍，Sensitive 和 Specificity 不变。但是此时预测为阳性的病例数为 7，其中只有 4 个正确，Precision=4/7=0.571。

图6

如果我们的阴性样本继续增加，保持 Sensitive 和 Specificity 不变，Precision 还将继续下降。若将阴性样本数量变为第一种情况的 100 倍，保持 Sensitive 和 Specificity 不变，Precision=4/104=0.04。

当面对极不均衡数据时，通常是阴性样本远多于阳性样本，我们发现 Specificity 常常会显得虚高。就好像上述的例子，Sensitive 和 Specificity 均为 0.8，但 Precision 仅有 0.04，即预测出的阳性中，有 96% 都是假阳性，这样就会带来用户的实际观感非常差。Specificity 虚高同时带来的影响是 AUC 也会显得虚高。同样，这个例子中的 Accuracy 也会显得很高，因为里面 TN 占了很大比例。

更加极端的例子，在阴性样本数量为阳性样本数量的 100 倍时，即使模型只预测阴性，它的 Accuracy 也大于 0.99。所以在数据极其不均衡时，我们选取 Precision、Recall 和 AP 值能够更好的反应模型的效果，同时也能更好的反应用户实际使用的体验。

实例解析

中山眼科发表了一篇糖网筛查的文章（http://care.diabetesjournals.org/content/early/2018/09/27/dc18-0147） ，文中提到模型的 AUC=0.955，Sensitive=0.925，Specificity=0.985。

通过文中对数据集的描述，我们知道测试集总共有 35,201 张图片（14,520 只眼），其中 904 只眼是阳性，按照比例估算，得阳性的图片约为 35201*904/14520 = 2192 张，阴性图片约为 35201-2192=33009 张，所以 TP=2192*0.925=2028，TN=33009*0.985=32514 张，FP=33009-32514-495 张，FN=2192-2028=164 张。混淆矩阵如表 3 所示，可算得 Precision=2028/(2028+495)=0.804。比 Specificity 有明显差距。

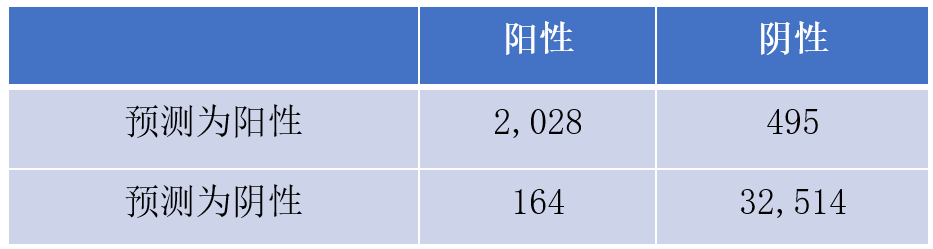
表格 3. 对中山眼科糖网模型混淆矩阵的估计

总   结

Sensitivity 和 Specificity 因为统计上与测试数据的先验分布无关，统计上更加稳定，而被广泛使用。但是当测试数据不平衡时（阴性远多于阳性），Specificity 不能很好地反应误报数量的增加，同时 AUC 也会显得虚高，这时引入 Precision 和 AP 值能更好的反应模型的效果和实际使用的观感。

---

喜欢这篇文章吗？记得点一下「好看」再走👇