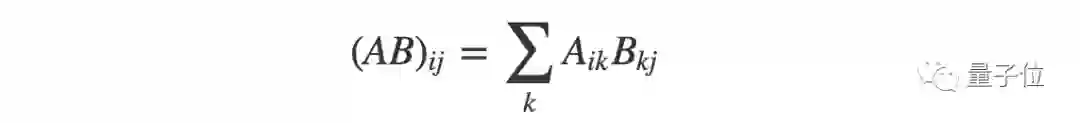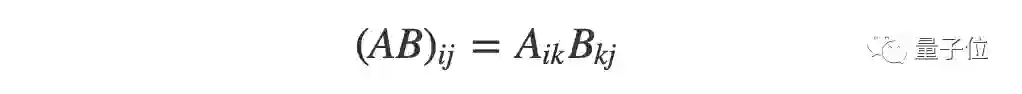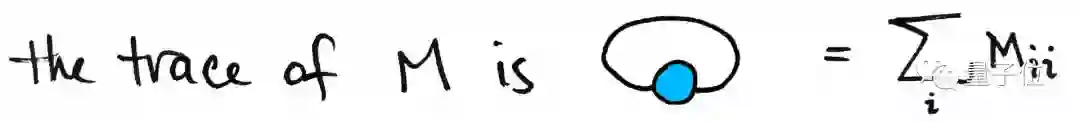给你一些点与线，只用动画就能看懂张量乘法，还能证明迹循环定理

晓查 发自 凹非寺
量子位 报道 | 公众号 QbitAI

钻研机器学习离不开线性代数，对于初学者来说，矩阵、向量还容易理解，到了张量这个概念就变得复杂了起来。

只因张量的乘法脚标太多，让人头大。而张量又是NumPy、TensorFlow等工具中必不可少的一种变量。如何理解它呢？

有一位来自纽约市立大学的小姐姐Tai-Danae，用手绘的方式介绍了一种表示张量乘法的直观方法，博客文章在初学者中广受好评。

之后，又有一位来自印度理工学院的小哥，用3blue1brown的数学动画工具manim，把张量乘法做成了动画，通俗演示了张量乘法的运算过程，浅显易懂。

下面就让我们来看看他们是如何图解张量运算的。

爱因斯坦求和约定

在了解张量运算前，先解释一下爱因斯坦求和约定。

爱因斯坦求和约定是爱因斯坦在研究相对论时提出的。由于相对论中经常用到张量乘积运算，爱因斯坦发明了一种简化写法，后来经常被人们所使用。

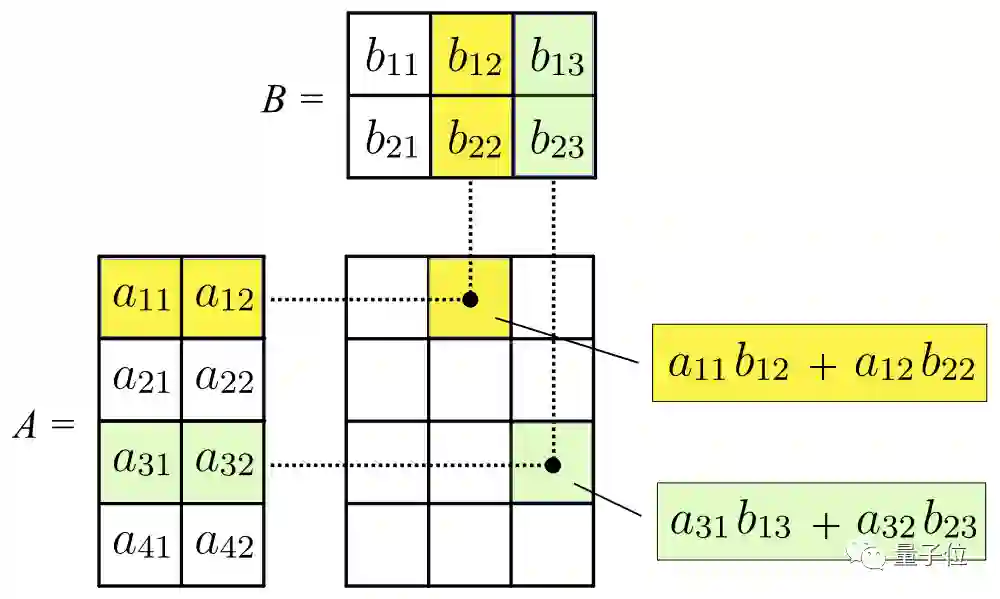
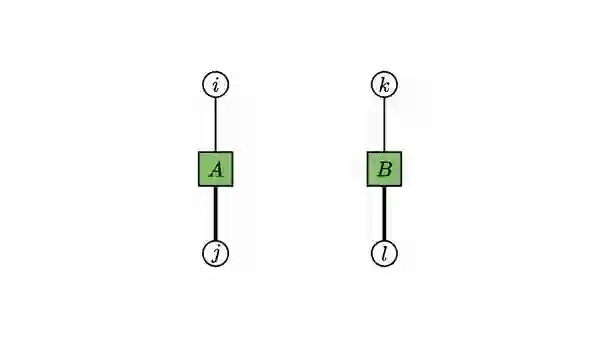
比如两个矩阵的乘积，定义为：

仔细观察，你可以发现矩阵A的第二个脚标和矩阵B第一个脚标相同，都是k。

即A的第k行乘以B的第k列对应元素。最后再把乘积相加，最后的结果里k消失了，所以对k求和的符号是完全多余的。

所以爱因斯坦规定，凡是遇到脚标相同的情况，就表示对这个脚标求和，把求和符号拿掉：

张量运算的公式因此得到了大大的简化。

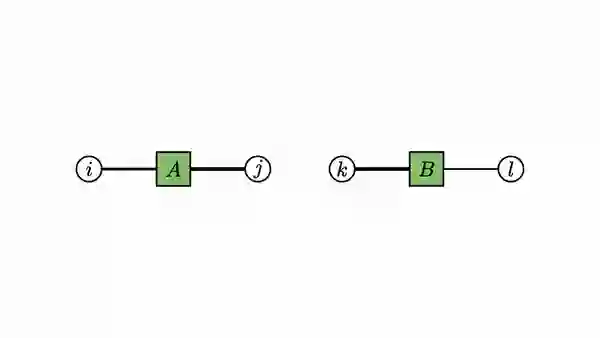
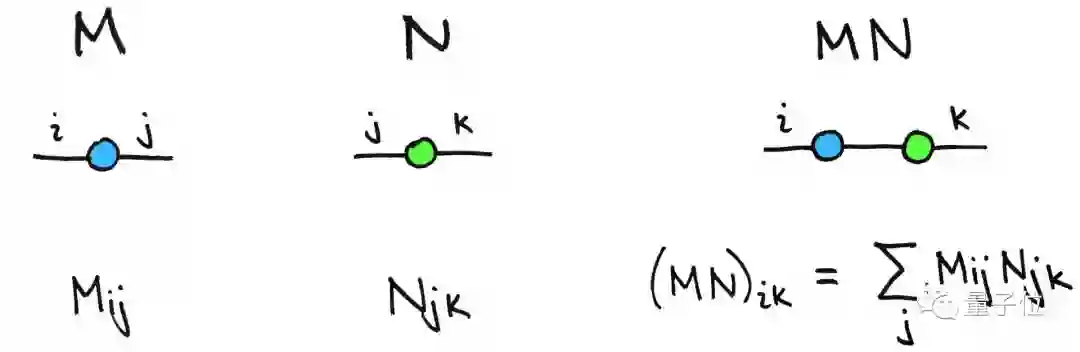
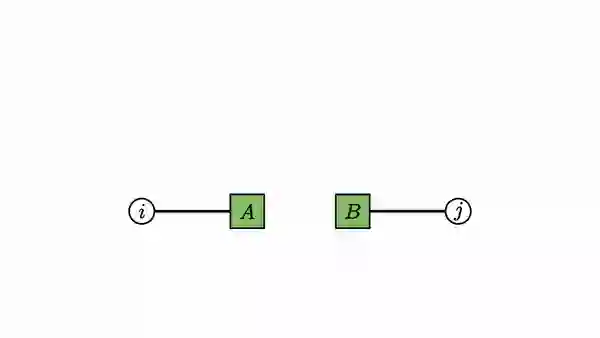
Rajat发现如果把矩阵的两个维度变成两个“触角”，把相同脚标的“触角”连接起来就是矩阵乘法：

用图表示张量

Rajat的张量乘积动画是自己领悟的，其实早在他之前，就已经有人引入了“张量网络”，它用一个节点和伸出去的几条线来表示张量。

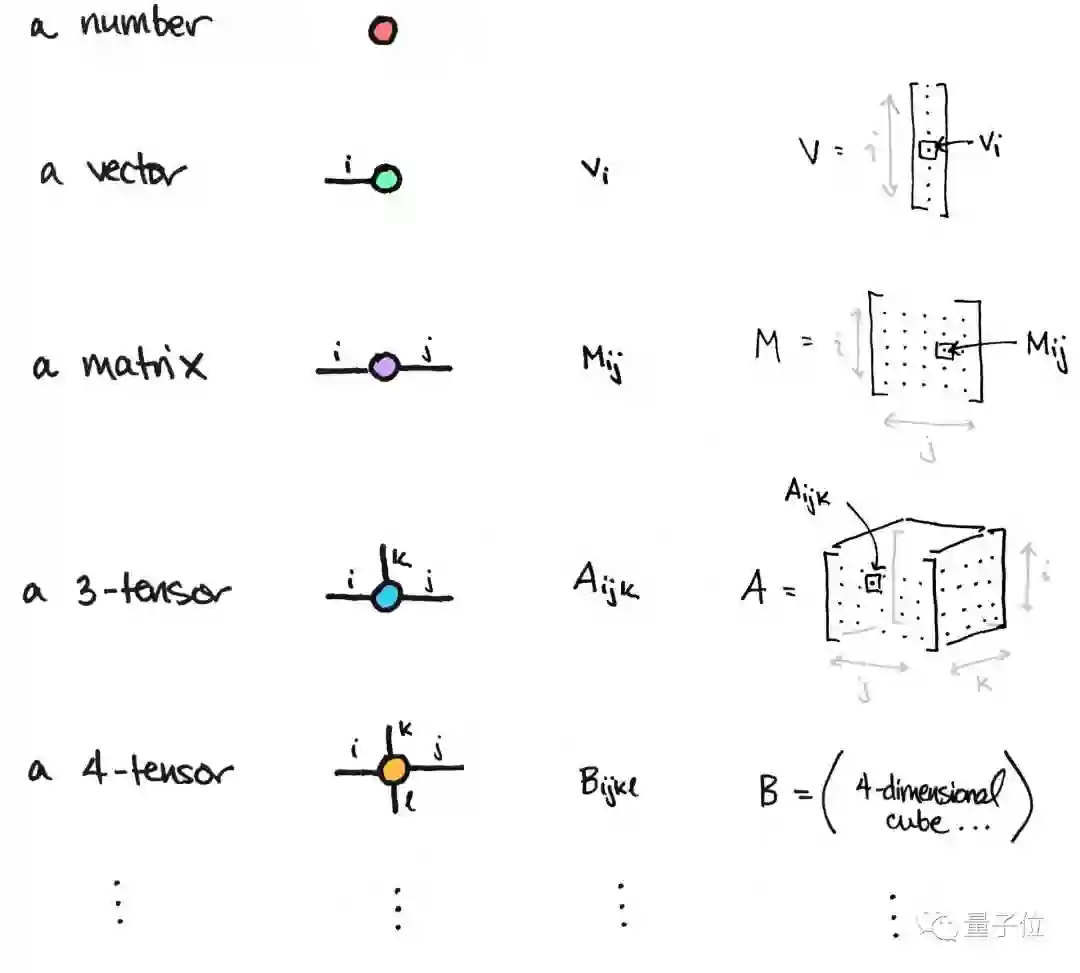
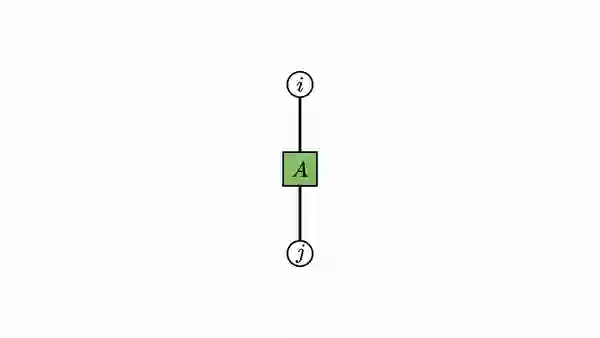
线的条数等于张量的阶数，矩阵是二阶张量，所以有两条线：

这是来自Tai-Danae手绘图。另外，标量可以看做零阶张量，向量可以看做一阶张量，矩阵是二阶张量，以此类推：

上面的矩阵乘法里，对于相同的脚标，就等于是一条线，于是两个矩阵M和N连接了起来：

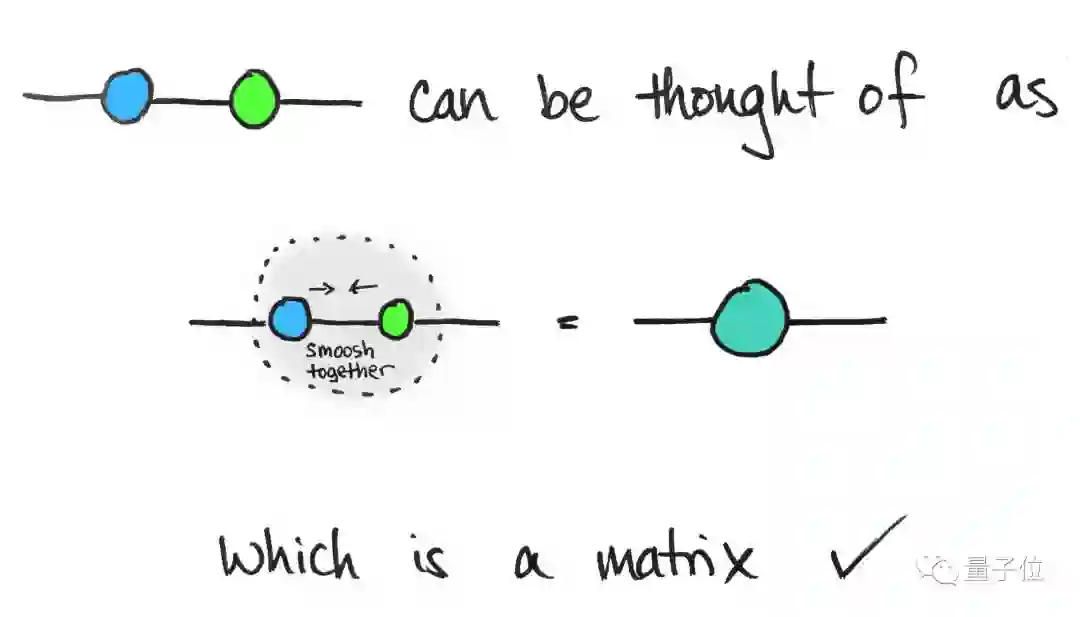
经过乘法运算后，得到的张量只有两个向外的边，可以把中间两个节点压缩成一个节点：

所以矩阵乘以矩阵仍然是一个矩阵（二阶张量）。

张量乘积的图表示

Rajat在“张量网络”概念的基础上，加入了一组视频，更生动地表示了几种常见的张量运算。

矩阵×向量：

矩阵×矩阵：

阿达玛乘积：

外积：

One More Thing

最后还有一种特殊情况，那就是矩阵的“迹”（trace）：

就是对M中行数与列数相等的元素求和，相当于把自己的两个“触角”连在一起，形成一个闭环。

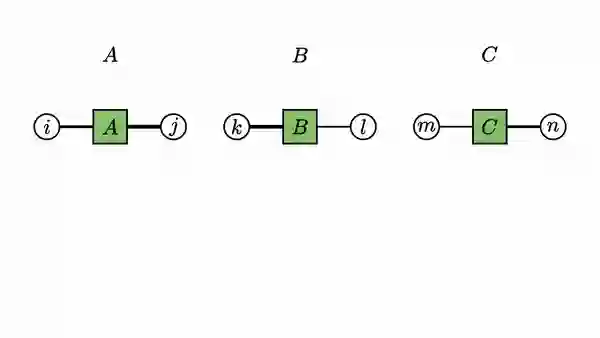
矩阵的迹满足如下的循环规律：

tr(ABC)=tr(CAB)=tr(BCA)

如果用图示法，就能更好地理解它：

参考链接：

https://rajatvd.github.io/Factor-Graphs/

https://www.math3ma.com/blog/matrices-as-tensor-network-diagrams

— 完 —

大咖齐聚！量子位MEET大会精彩回放

量子位 MEET 2020 智能未来大会精彩回放来袭！李开复、倪光南、景鲲、周伯文、吴明辉、曹旭东、叶杰平、唐文斌、王砚峰、黄刚、马原等AI大咖与你一起读懂人工智能。扫码观看回放吧~ ~

跟大咖交流 | 进入AI社群

量子位 QbitAI · 头条号签约作者

վ'ᴗ' ի 追踪AI技术和产品新动态

喜欢就点「在看」吧 !