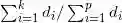数据分析师应该知道的16种回归技术:主成份回归
多元线性回归(MLR)可用来拟合因变量和多个预测变量之间的关系,然而当预测变量之间存在多重共线性或预测变量的个数非常多,使用MLR就会出现较大的误差。对于这个问题,可采用LASSO和松弛网络回归进行变量选择减少变量个数,也可采用岭回归缩减估计值减小估计方差,它们都是对目标函数进行调优来解决MLR的多重共线性或估计精度不足的问题。今天我们换一种思路通过坐标变换来改变预测变量间的相互关系同时减少回归变量的数量,然后对变换后的新预测变量进行回归,这就是主成份回归(PCR)的基本思想。
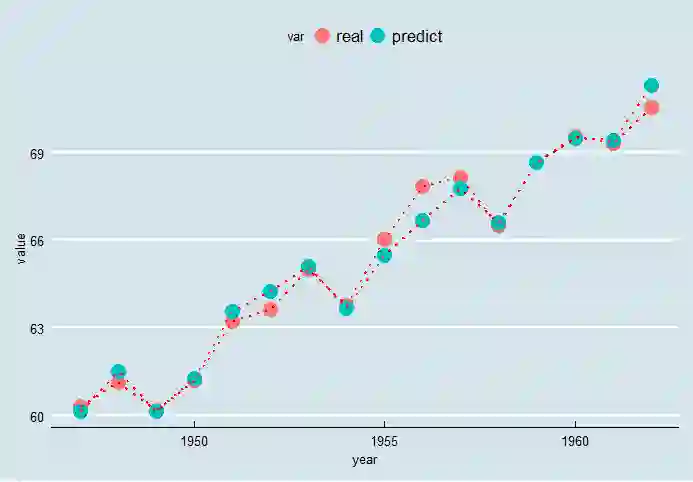
在传统的多元线性回归中,利用最小二乘(OLS)原则,回归系数的的估计值为:
其中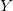

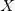
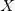
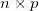

为进行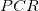
其中是由
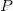

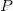
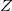
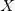
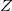
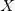
因为特征值越小多重共线性越严重,所以为了消除多重弄共线性,我们会舍弃特征值较小的主成份
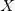
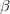
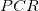

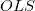

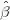
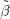
因此PCA的步骤为:
对
(标准化后)进行
,然后把主成份保存在
中
在主成份
上对
做拟合获得
的最小二乘估计
舍弃特征值较小的主成份同时设置
对应元素为0
通过关系式
获取
的原始估计值
最后一个问题是主成份个数的确定,一种简单的方法是舍弃特征值较小(远小于1)的主成份就可以。也可以使用下面三种客观评判标准:
方差贡献率:
为D的第
个元素
累计方差贡献率:
主成份标准差
主成份回归能进行特征提取但不能进行特征选择,因为每一个主成分都包含了所有特征
案例
下面我们对datasets包中的longley数据集进行主成份回归,该数据集包含从1947到1962的6项经济指标GNP国民生产总值,GNP.deflatorGNP物价折算指数,Unemployed失业人数,Population大于14岁人口数,Employed从业人数,Armed.Forces武装部队人数。现在我们想研究从业人数与其他指标之间的关系
使用prcomp进行PCA,
data1 <- longley[, colnames(longley) != "Year"]
X <- data1[,colnames(data1) != "Employed"]
#scale=T对数据集进行标准化
m1.pca <- prcomp(X, scale=T)
sml.pca <- summary(m1.pca)
library(ggplot2)
dtpc <- as.data.frame(cbind(pc=1:5,t((sml.pca$importance))))
names(dtpc)[2:4] <- c('sd','pv','cpv')
dtpct <- reshape2::melt(dtpc,id='pc', variable.name = "var")
ggplot(dtpct,aes(pc,value,group=var))+
geom_point(aes(colour=var),size=5)+
geom_path(lty = 3,colour='blue',lwd=1)+
geom_vline(xintercept=3,color='red',lty=4,lwd=1)+
ggthemes::theme_economist()
确定主成份个数为3,使用pls包进行PCR
library(pls)
pcr_model <- pcr(Employed~., data = data1,
scale = T, validation = "CV")
#scale = T对数据集进行标准化,validation = "CV"进行交叉验证。
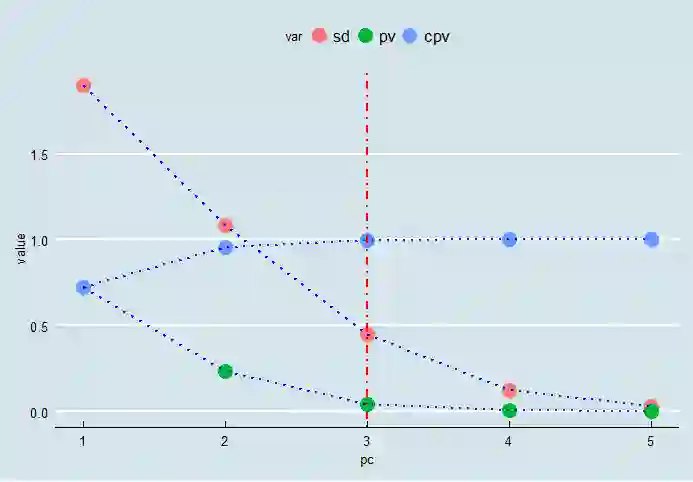
pred <- predict(pcr_model, data1, ncomp = 3);dimnames(pred)=NULL
dt <- data.frame(year=longley$Year,real=data1$Employed,predict=c(pred))
dtc <- reshape2::melt(dt,id='year', variable.name = "var")
ggplot(dtc,aes(year,value,group=var))+
geom_point(aes(colour=var),size=5)+
geom_path(lty = 3,colour='red',lwd=1)+
ggthemes::theme_economist()
推荐阅读
从零开始深度学习第8讲:利用Tensorflow搭建神经网络

长按二维码关注“数萃大数据”
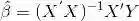
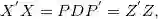
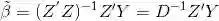
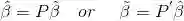
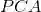 ,然后把主成份保存在
,然后把主成份保存在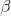 的最小二乘估计
的最小二乘估计 获取
获取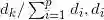 为D的第
为D的第 个元素
个元素