Top-N物品推荐算法评测设置回顾

会员服务 ·

Top-N物品推荐算法评测设置回顾

2020 年 11 月 17 日 机器学习与推荐算法

论文标题：Revisiting Alternative Experimental Settings for Evaluating Top-N Item Recommendation Algorithms

论文来源： ACM CIKM 2020

论文链接： http://arxiv.org/abs/2010.04484

1

引言

近十年里，top-N商品推荐是隐式反馈中一个被广泛研究的课题[1]，其目的是从大量数据中识别出用户可能偏爱的一小部分物品。各种top-N物品推荐算法已经被开发出来，特别是基于深度学习的研究取得了很大的进展[2]。

为了证明推荐算法的有效性，需要在基准数据集上建立可靠的评价实验。通常，这样的评估过程包括一系列对于数据集、指标、基线方法和其他方案的设置。由于每个设置步骤可以选择不同的选项，需要制定和设计适当的标准，以使实验设置标准化[3,4]。为此，有必要对近期研究中有分歧的实验设置进行系统的回顾。

在这篇论文中，对于不同的实验设置对评价top-N商品推荐算法的影响，我们设计了一个经验性的大规模实验。我们试图找出导致近期评测工作中出现分歧的重要评估设置[2,7]。具体来说，考虑三个重要的影响因素，即数据集分割、采样指标和数据领域选择。数据集分割是指利用原始数据构造训练集、验证集和测试集；采样指标是指用采样方法获得不相关物品来计算评测指标的结果；数据领域选择是指从不同领域中选择合适的数据集进行评估。

为了检验这三个因素的影响，我们在Amazonreview数据集[8]上进行了大量的实验，其中包含来自24个领域的1.428亿条用户交互记录。top-N物品推荐本质上是一项排序任务。与先前的工作[3，6]不同，本文并不关心特定方法的性能，而是研究一个特定的实验设置因素如何影响不同方法的总体排序。本文选取了8种具有代表性的推荐算法作为比较方法，包括传统方法和基于神经网络的方法。我们利用三种序列相关性指标来刻画排序结果的差异。

我们的实验得到了以下结论。首先，对于数据集分割，随机切分与时序切分产生了一定程度上不同的方法排序。数据集的切分方式应该取决于特定的任务。建议在一般情况下采用随机切分的方式划分数据集合，而对时间敏感的任务采用按照时序划分方式（如序列推荐）。第二，基于采样指标的表现排名与精确排名的相关性略弱，增加采样物品的数量会提高排序相关性程度。在使用采样指标时，研究人员应尽可能采样较多的不相关物品。最后，具有不同领域特征或稀疏程度的数据集合可能会产生不太相同的表现排名。一个较优的策略是选择能够涵盖多个领域、不同方面的代表性数据集。

2

实验设置与方案

2.1 实验设置

在这一部分中，我们描述数据集、比较方法和评估指标，来准备进行实验。

数据集。我们采用亚马逊产品评论数据集[8]进行评估，其中包含来自24个领域的1.428亿条评论。对于top-N物品推荐，每条评论被视为用户和某个物品之间的交互记录，而其余信息则被丢弃，比如文本和元数据。由于几种比较方法无法在有限的时间内对Book领域的数据集得出结果，因此为了提高效率，我们删除了这个领域。最后，我们使用来自其余23个领域的用户项交互数据作为最终数据集。我们进一步采用5-core的预处理方式，删除了不活跃的用户和不经常被点击的商品。

比较方法。我们选取了八种推荐算法，包括popularity，ItemKNN，SVD++ [9]和BPR [1]，DSSM [10]，NCF [11]，DIN [12] 和 GCMC [13]。在这八种方法中，popularity和ItemKNN主要基于简单的全局或物品特定的统计，SVD++和BPR利用矩阵分解技术，DSSM和NCF利用神经网络建模用户-物品交互，DIN通过关注现有行为来学习用户偏好，GCMC采用图神经网络进行推荐。这八种方法很好地涵盖了传统方法和基于神经网络的方法。在本文中，我们只考虑general item recommendation，而不考虑context-awarerecommendation或sequential recommendation。注意，我们的重点不是确定最佳算法，而是研究不同实验设置对最终表现排名的影响。

评价指标。Top-N项目推荐可以视为一项排序任务，排在前端的结果需要重点考虑。根据[4-14]，在下面的实验中，我们使用了四个指标：(1)顶部K个位置的截断精度和召回率(P@K and R@K)，(2)平均准确率(MAP)，(3)ROC曲线下面积(AUC)。我们还计算了另外两个指标的结果nDCG@K和MRR。它们与上述四个指标产生了相似的结果，我们省略了对应的实验结果。

2.2 实验方案

在本节中，我们将介绍用于比较top-N商品推荐的实验方案。

配置。我们引入“配置”一词来表示上述三个因素的不同选择的组合，即数据集分割，采样指标和领域选择。我们选择这三个因素是因为这些在最近的基于神经网络的方法文献中仍然存在一定的分歧（缺乏标准化的讨论）。注意，我们不会列举这三个因素的所有可能选项，我们只考虑近期研究中流行或有争议的选项。为了减少其他因素的影响，我们可能通过不同的选项单独报告结果，也可能根据先前的研究[3-6]将其设置为建议的选项。

相关测量。在给定配置的情况下，我们可以获得基于某种指标的八种比较方法的一个排序列表。我们采用三种排序相关性度量来刻画两个排序之间的相关性或相似度：

(1)Overlap Ratio at top-k positions (OR@k)；

(2)Spearman’s Rank Correlation (SRC)；

(3)Inversion Pair Count (IPC)。

选择这三种方法的理由如下。SRC刻画了整体排序的相关性，IPC提供了对SRC值的更直观的理解，对于商品推荐，排名靠前的位置需要更多关注，可由OR@k刻画。

实验步骤。给定一个指标，我们首先根据配置（用验证集优化）导出八种方法的表现排序。为了检验一个因素的影响，我们将通过考虑备选方案来生成多个配置。然后，利用上述指标计算两种不同配置下的表现排名之间的关联度。最后，相关结果将在23个数据领域上取平均值（除第4.3节之外）。

3

实验

在这一部分中，我们给出了与数据集分割、采样指标和数据领域选择三个因素相关的实验结果。当考虑一个因素时，我们会固定其余两个因素。也就是说，在两个配置进行比较的情况下，我们只改变所研究的因素，而将其余的设置设为相同的。

3.1 数据集切分分析

我们首先研究不同的数据集切分策略（即构建训练/验证/测试集）对表现排名的影响。

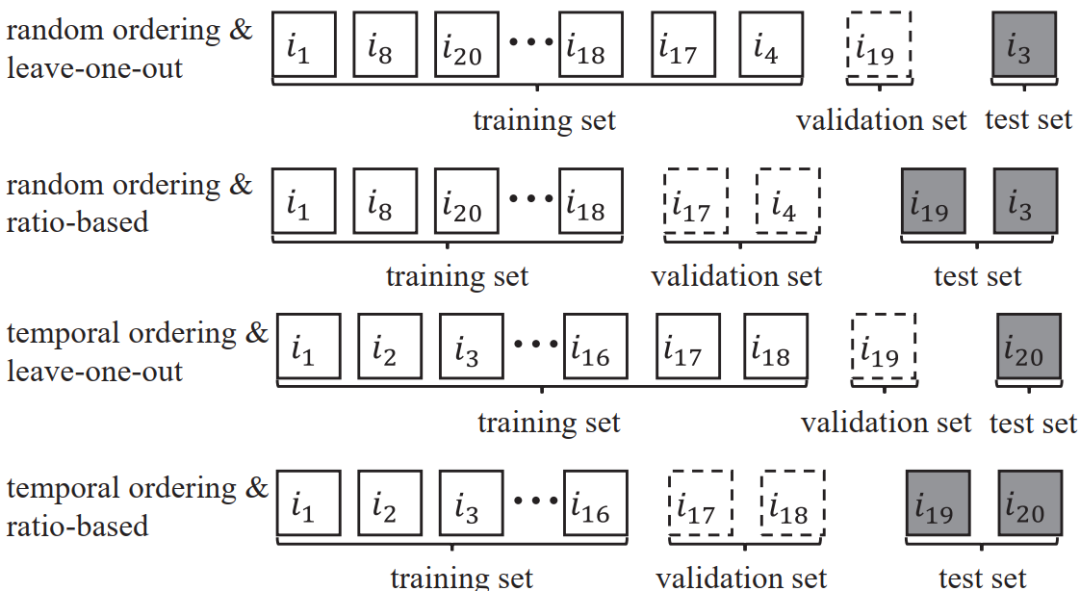
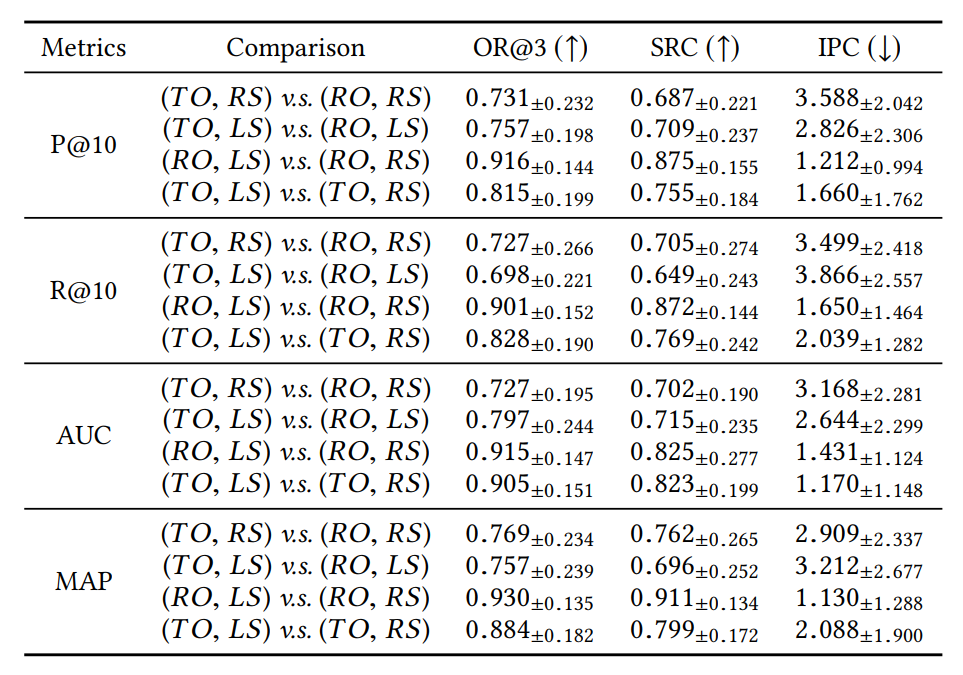
设置。 对于每个用户，我们首先使用两种方法组织用户的交互记录：(1) 随机排列（RO），随机选择商品；(2) 时序排列（TO），根据交互时间戳对商品进行排序。然后，可以使用以下两种常用方法拆分重新排序的用户项交互序列：(1)基于比率的分割（Ratio-basedSplitting, RS），根据预定比率将数据集分为三个部分，以进行训练，验证和测试，此处将比例设置为8：1：1。我们重复此过程五次，以生成不同的评估集，计算平均结果。(2)Leave-one-out分割（LS），选择一个物品作为测试集，另一个物品作为验证集，其余物品全部作为训练集。LS策略可以看作是RS的一个特例，当其中验证集和测试集都只包含一个项目。考虑到物品排序和切分方式，可以生成了四个组合，如图1所示。

图1：四种切分策略的说明性示例。用户与20个物品交互。项目i的下标表示与用户的交互顺序：较小的索引表示较早的交互时间。我们使用标准、划线和灰色框分别表示训练集、验证集和测试集。

结果。表1中给出了两种不同配置之间的比较结果。首先，与切分法（比率法或留一法）相比，物品排列方式（随机排列或时序排列）对表现排名的影响更为显著。对于每一个指标，表中前两行的相关性数值显著弱于最后两行的相关性数值。时序排列本质上应用于序列化推荐（Sequential recommendation）的设置。建议在一般情况下（尤其是评估时序不敏感的推荐算法）应采用随机排序，而在时序敏感的情况下（如序列化推荐）采用时序排列。第二，使用相同的物品排列方式，两种切分方法生成的算法排序非常相似（请参见每个度量的最后两行）。实际上，在最近的文献[8,11]中，留一法（leave-one-out）评测已经被广泛采用。我们建议在一般情况下使用基于比率的切分方式，以获得更准确的评估。然而，对于小数据集，留一法切分可以缓解数据稀疏，并且简化评测环节。

表1：数据集合切分不同配置的相关性比较。所有结果都是基于23个领域进行平均获得的。这里，“RS”和“LS”表示基于比率的分割和leave-one-out分割；“RO”和“TO”表示随机排列和时序排列。“↑”（“↓”）表示越大（小）效果越好。

3.2 采样指标分析

接下来，我们研究抽样指标（Sampled metrics，只使用一组采样不相关物品用于评测指标的计算）对表现排名的影响。

采样设置。对于测试环节，当物品集合很大时，将项目集中的所有未交互物品都作为候选对象是很费时的。所以，目前一种流行的方法是将采样一小部分不相关物品进行计算。这种方法称为采样指标[7]。我们考虑了两种采样策略：随机采样和流行度采样，即根据均匀分布或基于频率的分布对不相物品进行采样。我们进一步考虑使用三个不同数量的不相关样本，即{10，50，100}，这意味着一个真实物品将与10个、50个或100个采样获得的不相关物品配对。当我们采用leave-one-out法分割时，情况变为real-plus-N[3，6]。为了进行比较，我们将整个商品集（不包括真实物品）的排序作为参考排名。根据第4.1节，对于数据集切分，在所有比较配置中采用基于比率的数据集分割（用RS表示）和随机排序（用RO表示）。

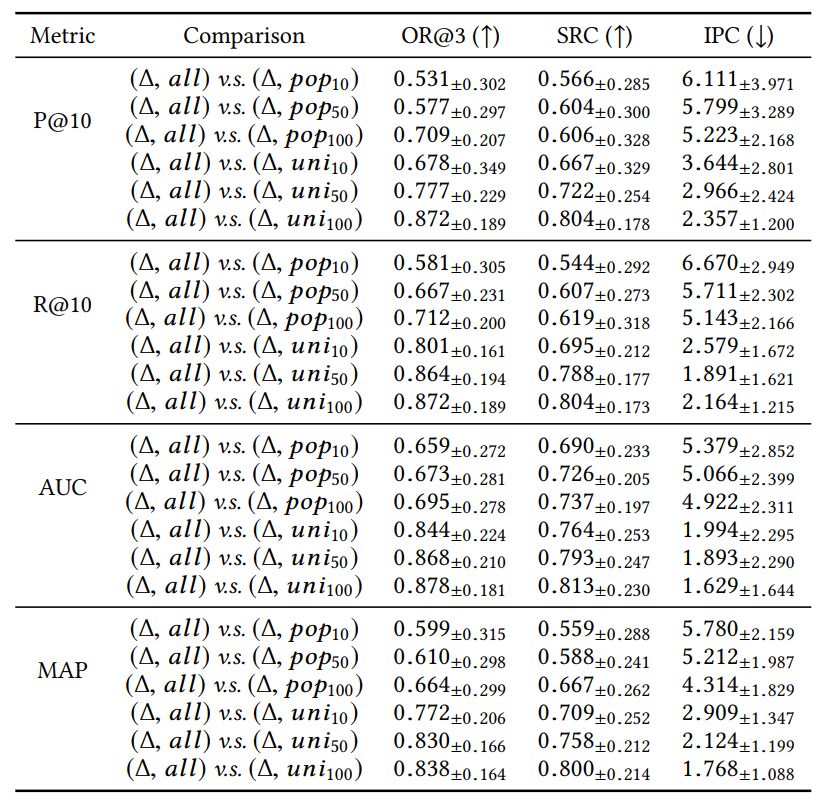
实验结果。表2展示了不同采样指标的相关结果，这些结果远小于表1中的数值。这表明使用采样指标对表现排名有较大影响。事实上，最近的研究已经讨论过这样一个问题[7]：采样指标可能得不到一致的排序。另一个观察的结果是，采样更多不相关的项目增加了采样指标和准确指标之间的相关度。最后，不同的采样策略可能会导致某些特定算法的表现动荡，从而严重影响表现排名。比较两种采样策略，均匀采样与整体排名的相关性似乎更高。一般来说，采样指标不应使用于小数据集。如果需要，我们建议采样更多不相关的物品（如[9]建议的1000个项目）。

表2：采样指标不同配置的相关性比较。表中结果对于23个领域进行了平均。“∆={RO，RS}”表示用于使用随机排序对于物品进行排列，使用基于比率的方法进行切分，“pop”/“uni”表示流行度/均匀采样，下标表示采样数量，“all”表示使用所有物品进行评测。

3.3 数据邻域选择分析

这里，我们考虑不同领域是否会导致不同的表现排名。这个问题对于回答如何选择合适的数据集进行评测很有用。

实验设置。给定两个领域，我们首先根据第4.1节和第4.2节中建议的设置（RO，RS，all）生成一个配置，然后基于某个指标获得每个领域下的表现排名。然后，我们计算了两个领域排名之间的Spearman’sRank Correlation得分。我们对所有指标的SRC得分取平均值。最后的分数用来衡量两个领域之间的相关性。

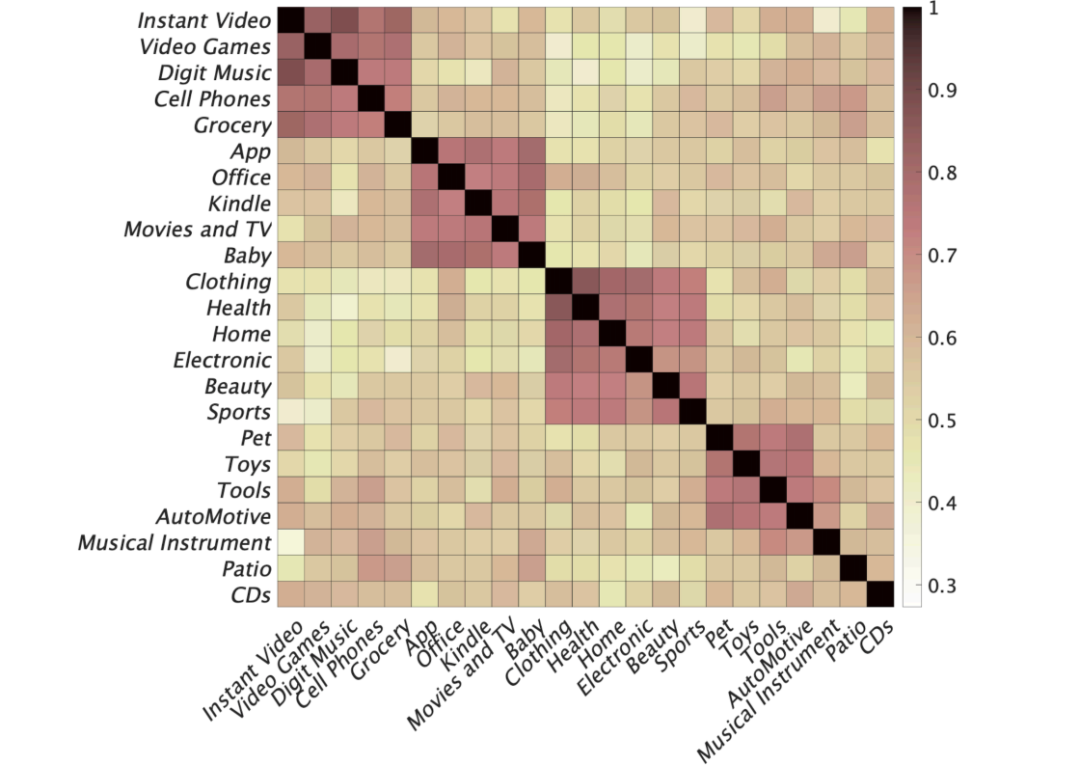
实验结果。图2显示了两个领域之间的平均相关结果。我们对行和列进行重新排序，以便可以在对角线上聚合较大的值。有趣的是，整个热度图似乎包含四大块（组），其中组内相关值高于组间相关值。结果表明，在相同的配置下，不同的领域可能会产生不同的表现排名。因此，评估时应考虑领域差异。通过对数据集的考察，我们发现领域特征（例如，第一组主要对应于数字产品）和稀疏程度（如用户-项目交互比率）似乎对相关结果有显著影响。使用多个来来自于不同领域、稀疏度不同的数据集是个好方法。这里，“领域”是指Amazon数据集的类别。我们将在未来的工作中使用更多的数据集来研究这个问题。

图2：成对领域相关性的可视化。每个单元格表示两个领域之间计算的相关性分数（颜色越深表示值越大）。

4

结语

我们通过实验检验了三个重要因素对于top-N推荐算法评测的影响。我们的实验结果为物品推荐算法提出了一些经验建议。首先，对于数据集切分，建议使用基于比例切分方式并且使用随机物品排列方式（非时序推荐任务），而leave-one-out切分方式可以用于较小数据集或者加快评测流程（如调参过程）。第二，应该谨慎使用采样指标。如果使用，我们建议加大采样样本数。第三，建议使用来自不同领域的多个数据集合作为评测数据集合。在未来的工作中，我们还将研究更多因素和数据集合来进一步完善当前的工作。

Reference

[1] S. Rendle, C. Freudenthaler, Z. Gantner, BPR:Bayesian Personalized Rankingfrom Implicit Feedback, in: UAI 2009, 452–461,2009.
[2] S. Zhang, L. Yao, A. Sun, Y. Tay, Deep Learning Based Recommender System: ASurveyand New Perspectives, ACM Comput. Surv. 52 (1) (2019) 5:1–5:38.
[3] A. Bellogín, P. Castells, I. Cantador, Precision-oriented evaluation ofrecommendersystems:an algorithmic comparison, in: ACM RecSys, 333–336, 2011.
[4] T. Silveira, M. Zhang, X. Lin, Y. Liu, S. Ma, How good your recommendersystemis?A survey on evaluations in recommendation, JMLC 10 (5) (2019) 813–831.
[5] H. Steck, Evaluation of recommendations: rating-prediction and ranking, in:ACM,RecSys 2013, 213–220, 2013.
[6] A. Said, A. Bellogín, Comparative Recommender System Evaluation: BenchmarkingRecommendationFrameworks,in: ACM RecSys, 129–136, 2014.
[7] W. Krichene, S. Rendle, On Sampled Metrics for Item Recommendation, in: ACMSIGKDD,2020.
[8] R. He, J. J. McAuley, Ups and Downs: Modeling the Visual Evolution of FashionTrendswith One-Class Collaborative Filtering, in: WWW 2016, 507–517, 2016.
[9]Y. Koren, Factorization meets the neighborhood: a multifacetedcollaborativeflteringmodel, in: ACM, SIGKDD 2008, 426–434, 2008.
[10] P. Huang, X. He, J. Gao, L. Deng, A. Acero, L. P. Heck, Learning deepstructuredsemanticmodels for web search using clickthrough data, in: CIKM, 2013.
[11] X. He, L. Liao, H. Zhang, L. Nie, X. Hu, T. Chua, Neural CollaborativeFiltering,in:WWW, 2017, 173–182, 2017.
[12] G. Zhou, X. Zhu, C. Song, Y. Fan, H. Zhu, X. Ma, Y. Yan, J. Jin, H. Li, K.Gai,DeepInterest Network for Click-Through Rate Prediction, in: ACM, SIGKDD,1059–1068,2018.
[13] R. van den Berg, T. N. Kipf, M. Welling, Graph Convolutional MatrixCompletion,CoRRabs/1706.02263.
[14] J. L. Herlocker, J. A. Konstan, L. G. Terveen, J. Riedl, Evaluatingcollaborativeflteringrecommender systems, ACM Trans. Inf. Syst. 22 (1) (2004) 5–53.