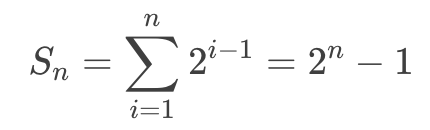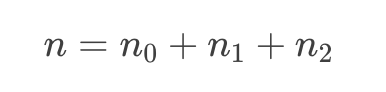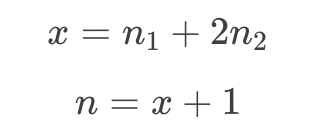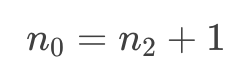二叉树的原理推敲与动手种树

作为数据结构的基础，树分很多种，像 AVL 树、红黑树、二叉搜索树....今天我想分享的是关于二叉树，一种基础的数据结构类型。

01

什么是树

在《数据结构》[注1] 中树有如下定义：

树是 n(n≥0) 个结点的有限集

在此我对上述定义做出如下解释：

当 n=0n=0 时，为空树，树的深度与高度均为 00，是树的一种特例；当 n>0n>0 时，为非空树，树的第一个结点，即深度为 11 的结点，我们称其为根结点，由根结点可以引出若干子树分支，同时子树分支可依此向下延伸，此时树的深度与高度也在变化，即树状图。

这里我们需要厘清树的深度与树的高度与其他树的术语：

• 树的深度：树中结点的最大层次

• 树的高度：从叶子结点开始定义，叶子结点为第一层，往上依次递增，直至根结点。

• 结点：树的结点包含一个数据元素以及若干指向其子树的分支

• 度：结点所拥有的子树数量

• 终端节点：度为0的结点称为叶子结点或终端结点

• 树的度：树中各结点度的最大值

• 层次：从根开始定义，根为第一层，依次递增

• 有序树：树中结点的各子树从左往右是有次序的，不可相互交换；反之则是无序树

• 森林：一棵非空树删掉根结点，即是森林

02

二叉树的概念引入

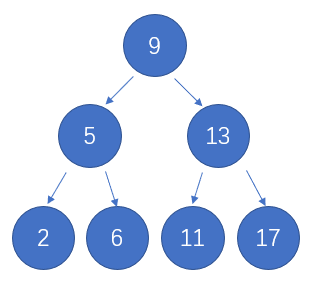
二叉树是由树演化而来的一种数据结构，上面所有术语均适用于二叉树。二叉树与树不同之处在于，树的每一个结点（除终端结点外）允许有若干子树分支；而二叉树只允许有左右两个子树分支，即不存在度大于 2 结点。

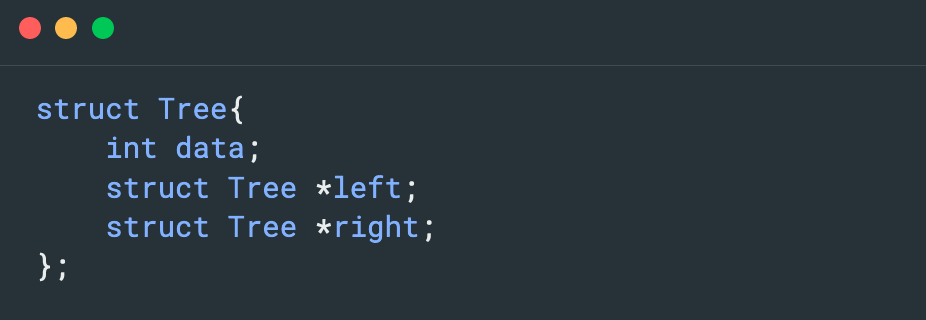
C语言示例:

上面的示例清晰地阐明了二叉树的结点是由一个数据元素和两个子树分支构成，需要明确的是，虽然终端结点没有指向任何子树，但它仍旧有往下繁衍的能力。

除此之外，二叉树还是一棵有序树，它的各个结点从左到右是依次有序可循的，且不可交换；它具有以下五种形态：

1. 空树

2. 仅有根结点

3. 左子树为空

4. 右子树为空

5. 左右子树均非空

当二叉树处于第五种状态，且设树的深度为 n，总结点数为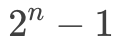 时，我们称其为满二叉树。

‍‍事实上还有另外一种也处于第五状态的树——完全二叉树。由于完全二叉树的定义在每个版本的教科书中均不相同，而笔者只接触过《数据结构 · 严蔚敏版》，因此摘录此书中对完全二叉树的定义：

深度为 k 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应时，称之为完全二叉树。

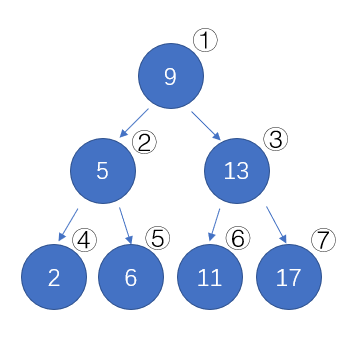
这段描述我读了两遍，方才理解其中的深刻含义，我们把深度为 3 的满二叉树的每个结点从上往下，从左往右进行编号：‍‍

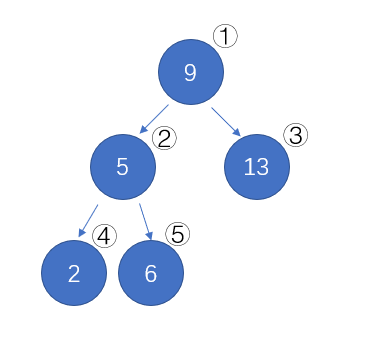
然后我们再定义一棵深度也为 3 的二叉树，该二叉树的 n 个结点（ n ≤ 7 ），当从 1 到 n 的每个结点都与上图中的编号结点一一对应时，这二叉树就称为完全二叉树。

举个例子，当  n = 5  时：

这便是完全二叉树。

因此我们还可以得到一个推论：满二叉树是完全二叉树，但完全二叉树不一定是满二叉树。

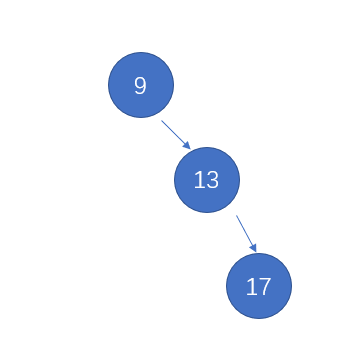
当二叉树处于第三种状态时，称其为右斜树。

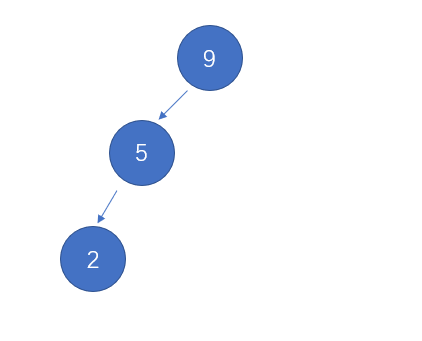
同理，处于第四状态为左斜树。

‍‍‍‍03

二叉树的性质总结

二叉树的第 i 层上最多有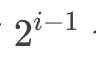个结点。此性质可通过上面满二叉树的图示推得

深度为 n 的二叉树，最多拥有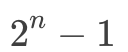 个结点。此性质可以通过数列求和得出：

设满二叉树深度为 n，叶子结点数必为

设任意一棵二叉树的叶子结点数为 n0 ，度为 1 的结点数为 n1，度为 2 的结点数为 n2；总结点数为 n。则有：

设分支的总边数为 x，则有：

联立上述三式可得：

即任意二叉树的叶子结点数为该树中度为 2 的结点数的总和加一。

设一完全二叉树具有 n 个结点，则其深度必为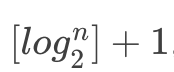，[x] 表示不大于 x 的最大整数，即向下取整。

04

手把手建立二叉树

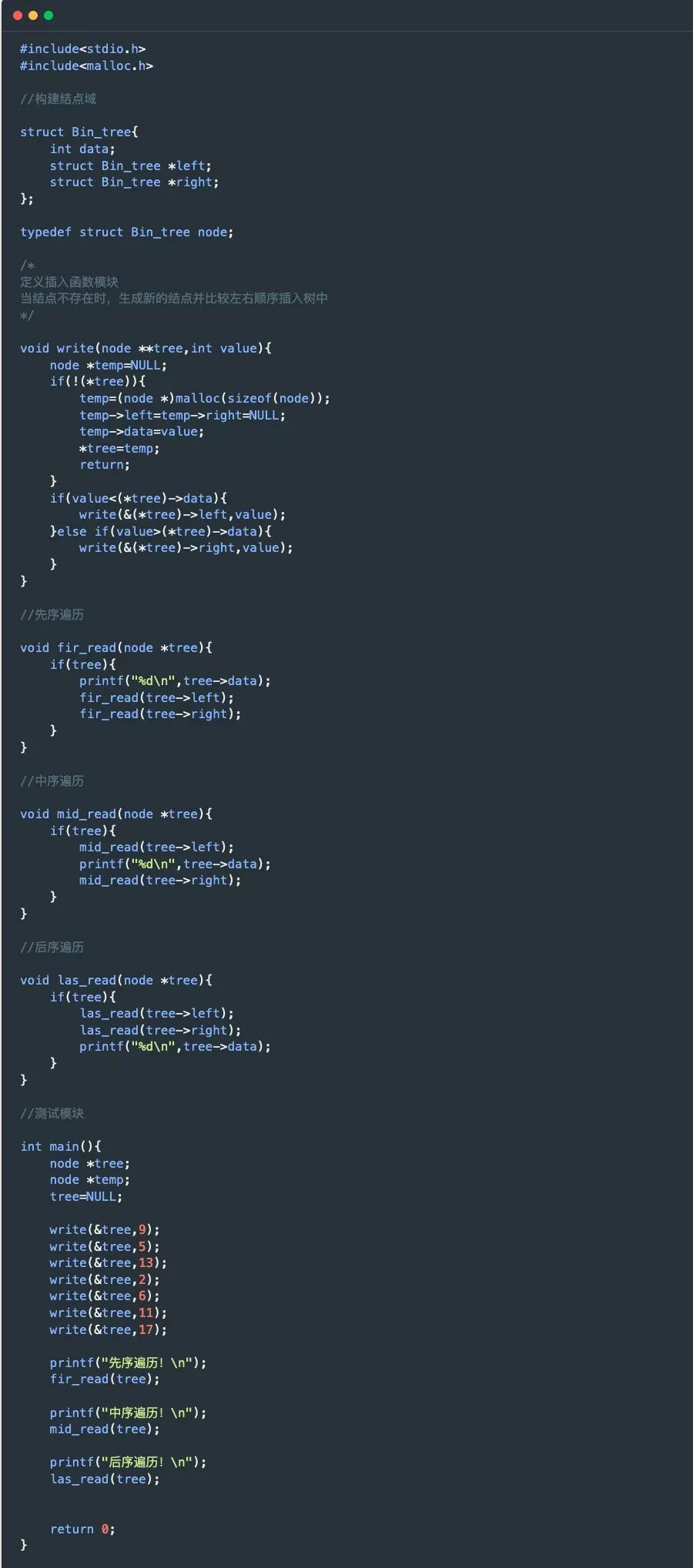
C 语言示例：

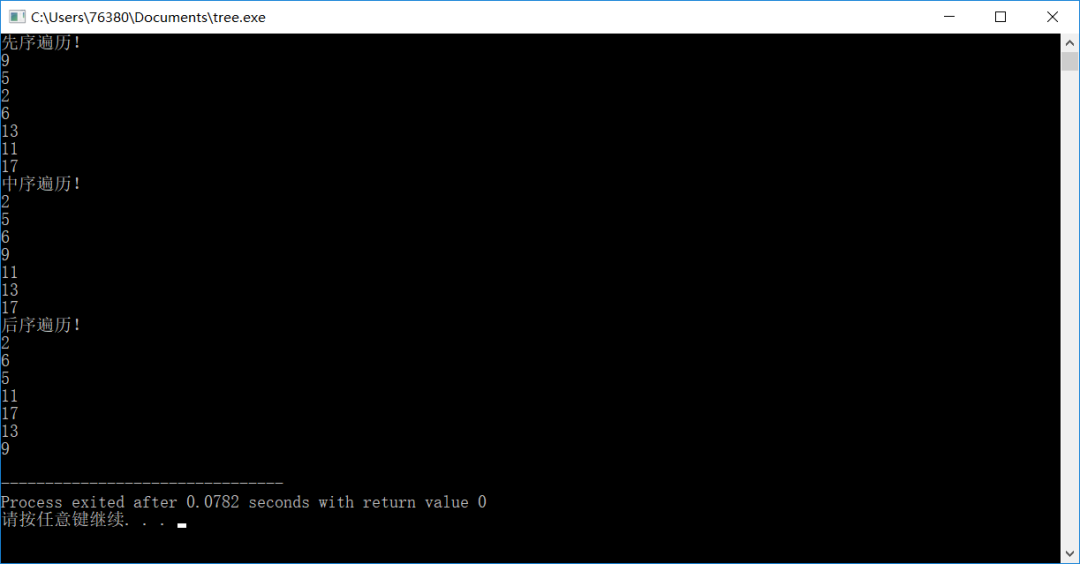
其中需要指明的是二叉树的三种遍历方法：先序遍历、中序遍历、后序遍历。

先序遍历

    即遍历顺序为“根—>左->右”。

中序遍历

    即遍历顺序为“左—>根—>右”，由于二叉树为有序树，因此中序遍历输出的值由小到大的。

后序遍历

    即遍历顺序为“左—>右—>根”。

还有一种遍历法，称为层序遍历，有兴趣的读者可以尝试着写一下。

参考资料

C 语言实现二叉树

注1：《数据结构 C 语言版》严蔚敏