机器学习(20)之Adaboost算法原理小结

微信公众号

关键字全网搜索最新排名

【机器学习算法】：排名第一

【机器学习】：排名第二

【Python】：排名第三

【算法】：排名第四

前言

在（机器学习(17)之集成学习原理总结）中，讲到了集成学习按照个体学习器之间是否存在依赖关系可以分为两类，第一个是个体学习器之间存在强依赖关系，另一类是个体学习器之间不存在强依赖关系。前者的代表算法就是是boosting系列算法。在boosting系列算法中， Adaboost是最著名的算法之一。Adaboost既可以用作分类，也可以用作回归。本文就对Adaboost算法做一个总结。

Boosting基本原理

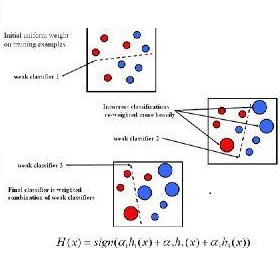
在（机器学习(17)之集成学习原理总结）中，已经讲到了Boosting算法系列的基本思想，如下图：

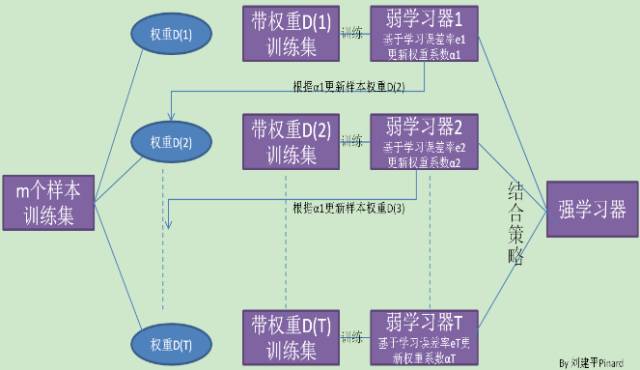
从图中可以看出，Boosting算法的工作机制是首先从训练集用初始权重训练出一个弱学习器1，根据弱学习的学习误差率表现来更新训练样本的权重，使得之前弱学习器1学习误差率高的训练样本点的权重变高，使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2.，如此重复进行，直到弱学习器数达到事先指定的数目T，最终将这T个弱学习器通过集合策略进行整合，得到最终的强学习器。　　

不过有几个具体的问题Boosting算法没有详细说明。

1）如何计算学习误差率e?

2 ) 如何得到弱学习器权重系数α?

3）如何更新样本权重D?

4 ) 使用何种结合策略？

只要是Boosting家族的算法，都要解决这4个问题。那么Adaboost是怎么解决的呢？

Adaboost基本思路

假设我们的训练样本是

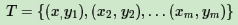
训练集的在第k个弱学习器的输出权重为

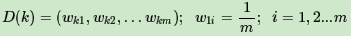
首先我们看看Adaboost的分类问题。

第一个问题：分类问题的误差率很好理解和计算。由于多元分类是二元分类的推广，这里假设我们是二元分类问题，输出为{-1，1}，则第k个弱分类器Gk(x)在训练集上的加权误差率为

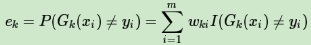
第二个问题：看弱学习器权重系数,对于二元分类问题，第k个弱分类器Gk(x)的权重系数为

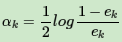
为什么这样计算弱学习器权重系数？从上式可以看出，如果分类误差率ek越大，则对应的弱分类器权重系数αk越小。也就是说，误差率小的弱分类器权重系数越大。具体为什么采用这个权重系数公式，我们在讲Adaboost的损失函数优化时再讲。

第三个问题：更新更新样本权重D。假设第k个弱分类器的样本集权重系数为D(k)=(wk1,wk2,...wkm)，则对应的第k+1个弱分类器的样本集权重系数为

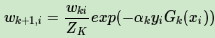
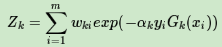
第四个问题：集合策略。Adaboost分类采用的是加权平均法，最终的强分类器为

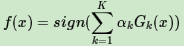
Adaboost的回归问题

（以Adaboost R2算法为准）

第一个问题：误差率的问题，对于第k个弱学习器，计算他训练集上的最大误差

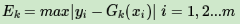
然后计算每个样本的相对误差

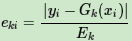
同时可以使用平方误差或者指数误差，平方误差如下所示

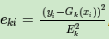
指数误差如下所示

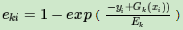
最终得到第k个弱学习器的误差率

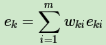
第二个问题：如何得到弱学习器权重系数α。这里有：

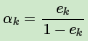
第三个问题：更新更新样本权重D，第k+1个弱学习器的样本集权重系数为

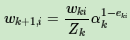
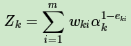
第四个问题：结合策略，和分类问题一样，采用的也是加权平均法，最终的强回归器为

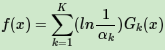
二元分类问题算法流程

输入为样本集

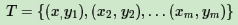
输出：{-1, +1}

弱分类器迭代次数K。

输出为最终的强分类器

算法流程

1) 初始化样本集权重为

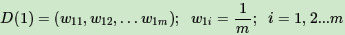
2) 对于k=1,2，...K:

    a) 使用具有权重Dk的样本集来训练数据，得到弱分类器Gk(x)

    b) 计算Gk(x)的分类误差率

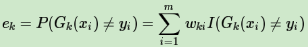
　c) 计算弱分类器的系数

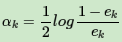
　d) 更新样本集的权重分布

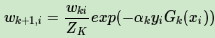
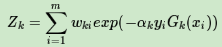
3) 构建最终分类器为：

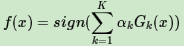
对于Adaboost多元分类算法，其实原理和二元分类类似，最主要区别在弱分类器的系数上。比如Adaboost SAMME算法，它的弱分类器的系数

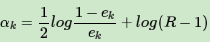
回归问题的算法流程

输入为样本集

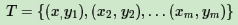
输出：{-1, +1}

弱分类器迭代次数K。

输出为最终的强分类器

算法流程

1) 初始化样本集权重为

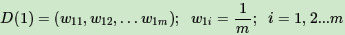
2) 对于k=1,2，...K:

    a) 使用具有权重Dk的样本集来训练数据，得到弱分类器Gk(x)

    b) 计算训练集上的最大误差

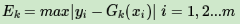
    c) 计算每个样本的相对误差:

        如果是线性误差，则

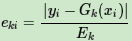
　　 如果是平方误差，则

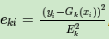
　　 如果是指数误差，则

　　

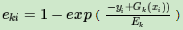
　d) 计算回归误差率

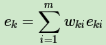
　e) 计算弱学习器的系数

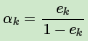
　f) 更新样本集的权重分布

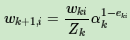
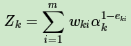
3) 构建最终分类器为：

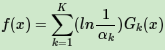
Adaboost正则化

为了防止Adaboost过拟合，我们通常也会加入正则化项，这个正则化项我们通常称为步长(learning rate)。定义为ν,对于前面的弱学习器的迭代

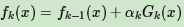
如果我们加上了正则化项，则有

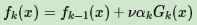
ν的取值范围为0<ν≤1。对于同样的训练集学习效果，较小的ν意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。

Adaboost 算法小结

理论上任何学习器都可以用于Adaboost.但一般来说，使用最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树，Adaboost分类用了CART分类树，而Adaboost回归用了CART回归树。

这里对Adaboost算法的优缺点做一个总结。

优点

1）Adaboost作为分类器时，分类精度很高

2）在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活。

3）作为简单的二元分类器时，构造简单，结果可理解。

4）不容易发生过拟合

不足

1）对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。

欢迎分享给他人让更多的人受益

参考：

1. 周志华《机器学习》

2. Neural Networks and Deep Learning by By Michael Nielsen

3. 博客园

   http://www.cnblogs.com/pinard/p/6133937.html

加我微信：guodongwe1991,备注姓名-单位-研究方向（加入微信机器学习交流1群）

招募 志愿者

广告、商业合作

请加QQ：357062955@qq.com

喜欢，别忘关注~

帮助你在AI领域更好的发展，期待与你相遇！