朴素贝叶斯分类器入门

论智

作者 | weakish

来源 | 论智

目前神经网络在机器学习领域应用十分广泛，其实除了神经网络，机器学习还包括其他技术，今天我们就来看一下机器学习的经典算法——朴素贝叶斯。

机器学习中经常需要对数据进行分类，比如过滤垃圾邮件。最简单的分类方法，就是预先定义一些规则，例如发件人、关键词、发信服务器和声称的地址是否一致等。但是，这样预先设定的分类方法实际效果并不是很好。

因为预先定义完善的规则需要花费大量的精力，而且不同用户需要的规则也是不一样的。另外，从产品的角度来说，很多用户可能并不具备设定一个完善的规则的能力或者精力。

其次，在利益的驱使下，垃圾邮件的发送者会不断改进自身的系统。因此，预先定义的规则哪怕再完善，也会逐渐过时。

而通过机器学习，能“自行”学习哪些邮件是垃圾邮件，不需要预先设定完善的规则，也能随垃圾邮件的变化而变化，遇强则强。

就拿根据关键词过滤垃圾邮件来说吧。传统的做法是预先定义出现哪些关键词就判定为垃圾邮件。那这个做法面对千变万化的垃圾邮件显然会很无力。如果通过机器学习来过滤的话，那我们可以一方面统计某些词语在正常邮件和垃圾邮件中出现的频率，根据两者的不同推断一封新邮件是正常邮件还是垃圾邮件；另一方面，我们又可以利用推断的结果反过来推断某些词语在正常邮件和垃圾邮件中出现的频率。这样，这个系统分类的邮件越多，识别效果就越好。

抽象一下，我们根据历史数据统计某一特征f在分类S和N中出现的概率（pSucc f S和pSucc f N），据此推断新数据属于S还是N。同时，我们根据新数据的分类，推断分类为S和N的邮件具有特征f的概率(pSucc S f和pSucc N f)，并进而调整pSucc f S和pSucc f N的值。

那么这个学习过程其实是辗转计算pSucc f S和pSucc S f这一组概率（N的情况同理）。

那pSucc f S和pSucc S f有什么关系呢？

我们尝试代入一个具体的例子来摸索一下。假设f代表邮件中出现了“正规发票”这个词，而S代表这封邮件是垃圾邮件。那么，直觉上，我们有：

1. 包含“正规发票”这个词的邮件是垃圾邮件的概率越大，相应地，垃圾邮件中包含“正规发票”这个词的概率也越大

2. 包含“正规发票”这个词的邮件是垃圾邮件的概率和垃圾邮件中包含“正规发票”这个词的概率并不相等

3. 包含“正规发票”这个词的邮件是垃圾邮件的概率大于垃圾邮件中包含“正规发票”这个词的概率

抽象上述表述，我们得到：

pSucc f S = coefficient * (pSucc S f) -- coefficient > 0
pSucc f S /= pSucc S f
pSucc f S > pSucc S f

一般地，f和S可以认为是两个先后发生的事件，pSucc f S可以认为是f发生后S发生的概率（这叫做条件概率或后验概率），pSucc S f同理。

交换f和S, 我们得到：

pSucc S f = coefficient * (pSucc f S) -- coefficient > 0
pSucc S f /= pSucc f S
pSucc S f > pSucc f S

我们看到，前 2 条没问题，第 3 条出现了矛盾。 这说明前面我们抽象不当，f和S并不是一般的两个事件，f和S还具有一些我们没有考虑的隐含性质。

回头看我们的直觉：

包含“正规发票”这个词的邮件是垃圾邮件的概率大于垃圾邮件中包含“正规发票”这个词的概率

这一条背后其实有一个假设：

碰到包含“正规发票”这个词的邮件的概率要小于碰到垃圾邮件的概率。

也就是说，p f < p S.

假设p f不为 0, 稍加变形，我们得到(p S) / (p f) > 1.

然后我们再将f和S抽象为一般事件，那么我们可以用(p S) / (p f)来表示

pSucc f S = coefficient * (pSucc S f)

中的系数coefficient，这样，当p f < p S的时候，就有pSucc f S > pSucc S f，反之，当p f > p S的时候，pSucc f S < pSucc S f。

这样我们就得到了pSucc f S和pSucc S f的关系：

pSucc f S = ((p S) / (p f)) * (pSucc S f)

显而易见，互换f和S没问题(假设p S不为 0)。

既然f和S是一般事件，我们不妨用a和b替换它们，以凸显其一般性：

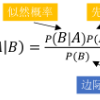
pSucc a b = ((p b) / (p a)) * (pSucc b a)

贝叶斯在18世纪发现了上面这个公式，因此它被称为贝叶斯定理（Bayes' theorem）。之所以称为定理，是因为贝叶斯是基于条件概率的定义推导出这个公式的。我们认为贝叶斯定理足够简单，因此跳过条件概率的定义直接讲贝叶斯定理。

回到垃圾邮件过滤的问题，前面我们提到：

一方面我们统计邮件中某些词语在正常邮件和垃圾邮件中出现的频率，根据两者的不同推断一封新邮件是正常邮件还是垃圾邮件，

这和贝叶斯定理有些差距。也就是说，实际上我们没有直接统计p f，而是分别统计了pSucc N f和pSucc S f.由于我们的分类系统不考虑无法判定的情况，因此一封邮件要么是正常邮件，要么是垃圾邮件，也就是说，p N + p S = 1.同时，既然pSucc N f表示已知一封邮件是正常邮件时，它具有特征f的概率，那么一封正常邮件具有特征f的概率就是(p N) * (pSucc N f)。同理，一封垃圾邮件具有特征f的概率就是(p S) * (pSucc S f)。因此一封邮件具有特征f的概率为：

p f = (p N) * (pSucc N f) + (p S) * (pSucc S f)

由此我们得到贝叶斯定理的一个变体，如果我们定义：

p -b = 1 - (p b)

那么贝叶斯定理就可以表述为：

pSucc a b =
    (p b) * (pSucc b a) /
    ((p b) * (pSucc b a) + (p -b) * (pSucc -b a))

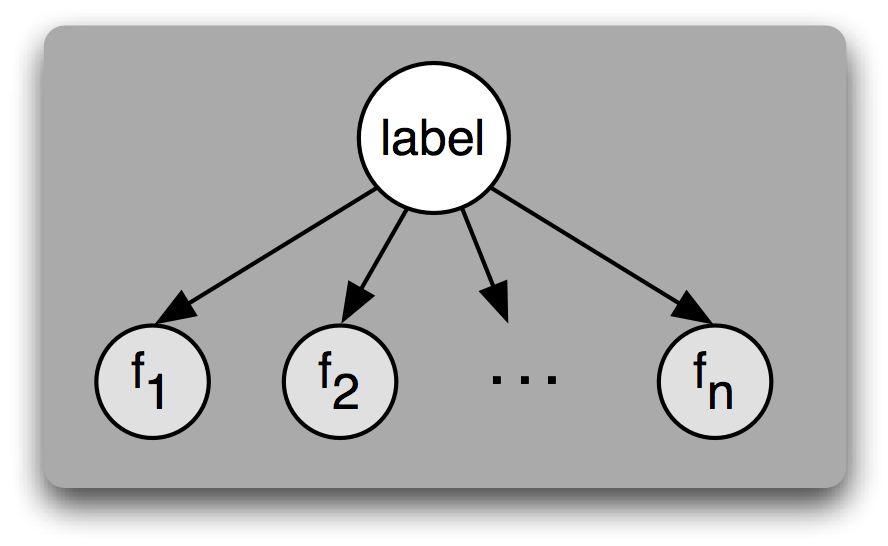
垃圾邮件过滤系统不可能只检查一个词，因此我们尝试推广到多个特征的情况：

pSucc [f1, f2 .. fn] S =
    (p S) * (pSucc S [f1, f2 .. fn]) / (p [f1, f2 .. fn])

其中，p S和p [f1, f2 .. fn]都很容易统计，而pSucc S [f1, f2 .. fn]的计算复杂度很高，特别是，S中同时具有[f1, f2 .. fn]的样本可能很少（稀疏），那训练的效果就很差了。

那怎么办呢？

我们可以假设[f1, f2 .. fn]的每一项都是独立事件。这样，pSucc S [f1, f2 .. fn]就可以化简为

(pSucc S f1) * (pSucc S f2) * .. * (pSucc S fn)

这样我们就只需要独立计算分类为S的情况下具有某一个特征的概率了，避免了样本稀疏的问题，同时，每一项都可以分布式地跑。

上面的式子中，如果某一项没有出现过，也就是说，分类为S的情况下训练集的数据中不存在具有某特定特征的样本，那一项的条件概率会为0，从而导致最后相乘的结果为0，也就是将其他各项的概率消除。为了避免这个问题，我们可以强行将概率为0的项修正为一个小概率，比如 0.01，具体数值无关紧要，因为以后如果训练集中新增了相应的样本，这个概率会自动得到修正的。当然，这样有点粗暴。更合理的做法是所有的样本数都加1，并相应增加总数，这样原本为0的样本数就变为1，避免了概率为0的情况。因为训练集一般都很大，所以样本数加1没什么影响。这种做法称为拉普拉斯平滑（Laplacian Smoothing）。当然，如果有必要，也可以改为加上一个小于1的正数。

别忘了，前面我们为了简化运算量，假设[f1, f2 .. fn]的每一项都是独立事件，这个假设可不一定成立。因此这个算法叫做幼稚贝叶斯分类器或者朴素贝叶斯分类器（Naive Bayes Classifier）。这个名称就是强调独立事件的假设不一定成立。

尽管独立事件的假设常常是不准确的，但朴素贝叶斯在实际工程中出乎意料地好用。因为很多应用并不在乎精确的类概率，只关心最后的分类结果。比如垃圾邮件过滤，只需要判断是否是垃圾邮件，并不需要在用户界面显示“本邮件有 87.53% 的概率是垃圾邮件”之类的信息。

本文系论智编译，转载请联系本公众号获得授权。