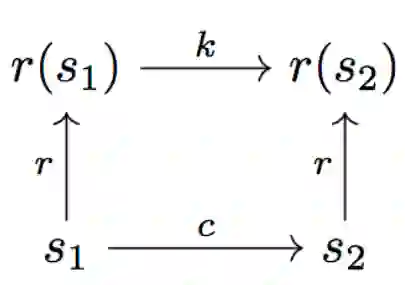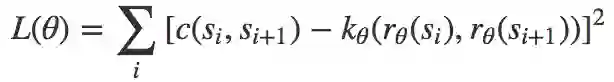强化学习表示空间中的规划

作者：Jacob Andreas

编译：weakish

编者按：Microsoft Semantic Machines资深研究科学家、UC Berkeley计算机科学博士Jacob Andreas以控制问题为例，讨论了在强化学习的表示空间中引入规划能力的思路。

以神经网络为参数的智能体（例如Atari玩家智能体）看起来普遍缺乏规划的能力。蒙特卡洛反应式智能体（例如原始深度Q学习者）明显是个例子，甚至于具备一定隐藏状态的智能体（比如NIPS的MemN2N论文）看上去也是这样。尽管如此，类似规划的行为已成功应用于其他深度模型，尤其是在文本生成上——集束解码，乃至集束训练，看上去对机器翻译和图像描述而言不可或缺。当然，对处理并非玩具级别的控制问题的人而言，真实的规划问题无处不在。

任务和运动规划是一个好例子。有一次我们需要求解一个持续控制问题，但是直接求解（通过通用控制策略或类似TrajOpt的过程）太难了。因此我们转而尝试高度简化、手工指定的问题编码——也许是丢弃了几何信息的STRIPS表示。我们解决了（相对简单的）STRIPS规划问题，接着将其投影回运动规划空间。该投影可能不对应可行的策略！（但我们想让在任务空间中可行的策略在运动空间中尽量可行。）我们持续搜索计划空间，直到找到在运动空间中同时奏效的解。

其实这不过是一个由粗到细的剪枝计划——我们需要可以丢弃明显不可行的规划的低成本方法，这样我们可以将全部计算资源集中到确实需要模拟的情形上。

如图所示：

上图中，r为表示函数，c为成本函数（我们可以将其视为用0-1表示可行性判断的函数），k为“表示成本”。我们想要确保r在运动成本和任务成本上“接近同构”，也就是c(s₁, s₂) ≈ k(r(s₁), r(s₂))。

就STRIPS版本而言，假定我们手工给出r和k。不过，我们可以学习一个比STRIPS更好的求解任务和运动规划问题的表示吗？

从规划样本中学习

首先假定我们已经有了训练数据，数据为成功的运动空间路点序列(s₁, s₂, …, s^*)。那么我们可以直接最小化以下目标函数：

最容易的情形是表示空间（r的对应域）为ℝ^d；这时我们可以操作d以控制表示质量和搜索表示空间的成本之间的平衡。

问题：如果我们只观测到常数c（如果只看到好的解，可能会出现这种情形），那就没有压力学习不那么微不足道的k。所以我们也需要不成功的尝试。

解码

给定训练好的模型，我们通过以下步骤求解新实例：

1. 从表示空间中取样一个满足r(s^*) ≈ r_n的成本加权路径(r₁,r₂, ..., r_n)。

2. 将每个表示空间转换r₁ → r₂映射到运动空间转换s₁ → s₂，且满足r(s₂) ≈ r₂。（如果r是可微的，那么这很容易表达为一个优化问题，否则需要麻烦一点表达为策略。）

3. 重复上述过程，直到其中之一的运动空间解可行。

在涉及计算路径的每一个步骤（不管是在r-空间还是在s-空间），我们都可以使用范围广泛的技术，包括基于优化的技术（TrajOpt），基于搜索的技术（RRT，不过大概不适用于高维情形），或者通过学习以目标状态为参数的策略。

直接从任务反馈学习

如果我们没有良好的轨迹可供学习，怎么办？只需修改之前的上面两步——从随机初始值开始，展开包含预测的r和s序列，接着生成由预测值r和s构成的序列，然后将其视作监督，同样更新k以反映观测到的成本。

提示性搜索

到目前为止，我们假设可以直接暴力搜索表示空间，直到我们接近目标。没有机制强制表示空间的接近程度同样接近于运动空间（除了r可能带来的平滑性）。我们可能想要增加额外的限制，如果根据定义r_i距离r_n不止3跳，那么||r_i − r_n||>||r_i+1−r_n||。这立刻提供了在表示空间中搜索的便利的启发式算法。

我们也可以在这一阶段引入辅助信息——也许是以语言或视频形式提供的意见。（接着我们需要学习另一个从意见空间到表示空间的映射。）

模块化

在STRIPS领域，定义一些不同的原语（如“移动”、“抓取”）是很常见的做法。我们也许想给智能体提供类似的不同策略的离散清单，清单上的策略列出了转换成本k₁, k₂, …。现在搜索问题同时牵涉（连续地）选择一组点，和（离散地）选择用于在点之间移动的成本函数/运动原语。这些原语对应的运动可能受限于配置空间中某个（手工选取）的子流形（比如，仅仅移动末端执行器，仅仅移动第一个关节）。

感谢Dylan Hadfield-Menell关于任务和运动规划的讨论。

原文地址：http://blog.jacobandreas.net/planning-representations.html