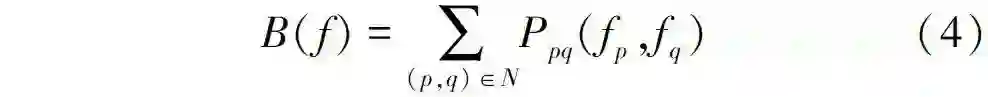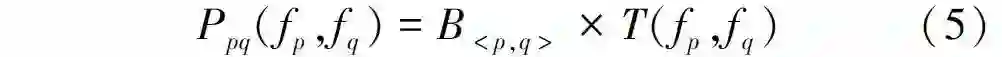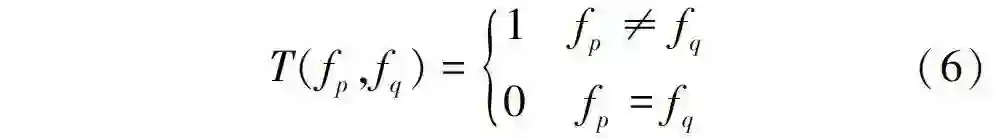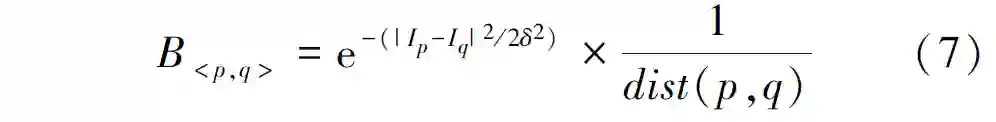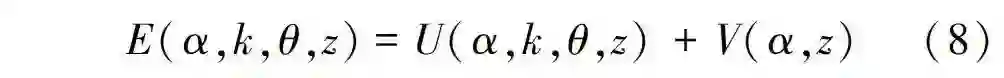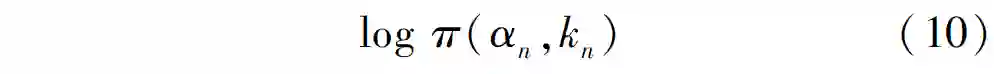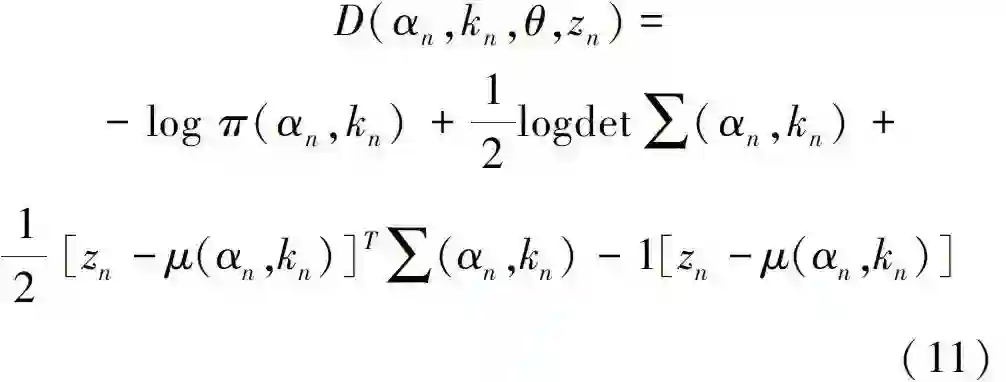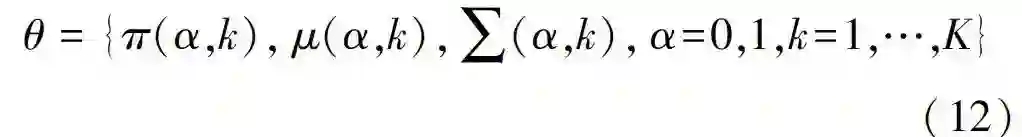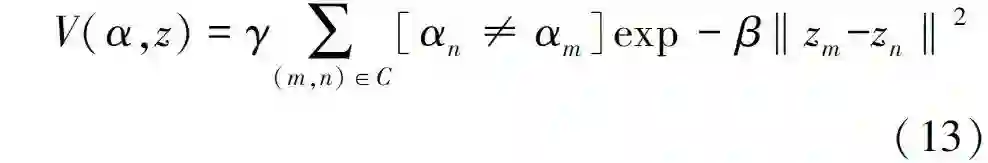实战|基于图割算法的木材表面缺陷图像分析
鉴于图割方法的明显优势,白雪冰及其团队采用Graph Cuts算法和Grab Cut算法分别对木材表面的单目标和多目标缺陷图像进行分割试验,以总结传统图割方法的不足和改进算法的优点。
针对传统Graph Cuts算法只能针对灰度图像进行分割、运行时参数的选择比较复杂,并且存在该算法效率和精度较低的缺陷,采用这两种方法分别对3种木材表面缺陷活节、虫眼和死节图像进行分割实验。为了验证Grab Cuts方法的适用性,用含有多个缺陷目标的木质板材图像做了图像分割验证。
结果表明:缺陷图像的目标和背景的种子点选取直接影响Graph Cuts算法的分割结果,Graph Cuts算法的计算效率较低,分割时间较长,对相邻像素间的区分度较差,分割结果不理想。改进后的Grab Cut算法是迭代的Graph Cuts,该方法虽然在图像分割前也需要人工画定初始化矩形框,但操作相对简单,分割结果能够得到完整的闭合缺陷区域边界,且不受木材表面缺陷的类型、数量、尺寸和缺陷形状的影响,分割效果好,分割速度快,抗噪性强,对灰度图像和彩色图像都可使用。
图割算法
1.1 Graph Cuts 算法的原理
图割(Graph Cuts)交互式图像分割算法是一种基于图论的组合最优化方法,其基础是最大流算法,将图像分割问题转化成能量函数的最小化问题,通过最小化能量函数,从而实现图像的最优分割。首先,建立能量函数:
E(L) = R(L) + λB(L) (1)
式中:R(L)是区域项,表示区域属性;B(L)是边界项,表示边界属性;λ 为平衡因子,当λ 较小时,边界项可忽略,当λ 较大时,图像的所有点被赋予相同标记。
设P={p1,p22,…,pN2 } 是像素集合,L={0,1}是像素标记集合,0表示背景,1表示目标;像素的标记可以表示为从P到L的映射, 记作fp={fp| fp ∈L}。
因此,式(1)中的区域项表示为R(f)=Rp(fp ),p ∈ P,用Rp(fp) 来进行判定像素p分配给某种标记的可能性。通常对能量函数中的区域项取概率的负对数,且将预定义的种子点作为目标和背景的采样,以此估计目标和背景的灰度直方图分布,对于目标/背景的二值分割,区域项可表示为:
式(2)代表了像素p分配给目标区域的可能性,式(3)代表像素p分配给背景区域的可能性,随着可能性的增大, Rp(•) 的值会减小,从而可通过最小化能量函数来实现对图像的准确分割。式(1)的边界项可表示为:
式中: p和q为相邻像素,边界项体现图像边界像素值的不连续性; N为4邻域或8邻域系统。通过变分模型可以将式(4)写为:
其中, T(fp ,fq ) 为指标函数,满足 :
B < p,q > 为对像素p 、q不连续性的惩罚值:
式中:Ip 、Iq为像素p、q的灰度值; dist(p,q)是p和q的距离; δ为图像噪声。p和q越相近,则B < p,q >越大;若p和q相差较大,则B < p,q >趋近于0 。当B < p,q >的值较小时,两个像素会更易于分给不同的区域,这时图像分割得到最小的能量值。
Graph Cuts算法源于图论,通过最小化能量函数实现图像分割 。首先要对(1)的能量函数公式来构造网络图,把表示带有非负边权的无向图G= (V,E)作为图像,其中V为顶点集,与其相对应图像的边集为像素点集P,E。V含有两个特殊的顶点,其一称为源节点S(代表目标),其二称为汇节点T(代表背景),因此构造的网络图又称为S-T图。
1956年Ford等提出了网络流理论,论证了网络图中的最大流与最小流的等价性。式(1)的能量函数可通过最大流/最小割定理来求解,具体包括增广路径(augmenting paths)法和推进⁃重标记(push-relabel)法。本试验采用后者。
1.2 Graph Cut算法的原理
由于Graph Cuts算法只能分割灰度图像,且参数选择复杂,效率和分割精度较低。因此,Blake等从以下三方面进行了改进,形成Grab Cut算法 :
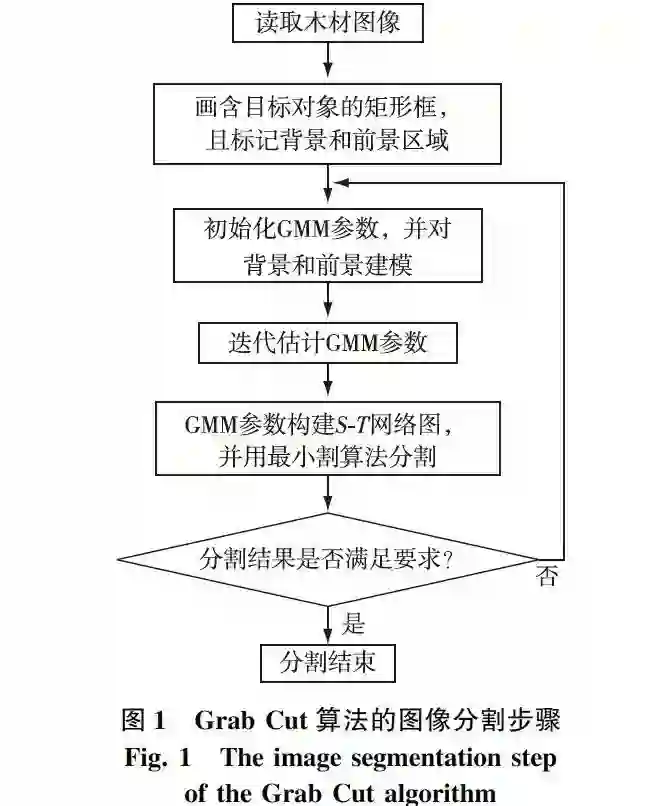
1) 弃用灰度直方图,转而选用高斯混合模型(GMM 模型)来描述颜色信息的概率分布,实现彩色图像分割;
2) 在GMM模型参数估计过程中,采用可进化的迭代算法取代一次最小估计来完成能量最小化,提高了分割精度;
3) 为了降低用户交互的工作量,通过非完全标号(incomplete labeling)方式(交互中没有指定明确的目标)进行像素标记。该方法只需用户在目标周围画一个矩形框即可。
Grab Cut算法把图像表示为矢量Z= {z1,z2,…,zn,…,zN} ,这样便将图像的分割转化为求每个像素对应的不透明度数组α= {α1,α2,…,αn,…,αN }αN|(αn ∈[0,1]), αn取值为0(背景)或者1(目标),图像目标与背景模型分别用k维的全协方差矩阵GMM表达,通常k=5。向量k={k1,k2,…,kn,…,kN}为每个像素的独立GMM(目标或背景的参数,参数来自目标还是背景,取决于αn的值 ,从而使目标提取问题转化为能量函数的最优化问题,然后采用图割方法求解。
对于RGB空间上的彩色图像,吉布斯(Gibbs)能量函数为:
式中:E为能量;U代表数据项; V代表光滑项; α代表不透明度; θ代表图像目标和背景的灰度直方图; z代表图像灰度值数值。数据项U定义为:
其中, D(αn,kn,θ,zn) = -log p(zn|αn,kn,θ) -
式中: π(•) 代表该高斯模型的样本数在总样本中的混合权重系数; p(•)代表高斯概率分布。所以数据项又可表示为:
则高斯混合模型的参数模型为:
其中: π(α,k)代表每个高斯概率分布的样本数在总样本数中的权值; μ(α,k) 代表高斯模型的均值;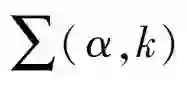
平滑项V可以采用RGB彩色空间的欧几里德距离求得:
式中:C代表相邻像素对; γ为自适应λ参数; β为常数项。
若把一个更接近真实情况的标记赋予某个像素,则将会惩罚更小的数据项,这样会使总能量函数减少,不断地迭代,最终收敛至最优分割,这样便将Grab Cut算法的图像分割问题转化成求解最小割的问题。
Grab Cut算法的图像分割步骤如图1所示。
木材表面缺陷图像分割实验
2.1 基于Graph Cuts算法的木材表面缺陷图像分割
本试验采用的计算机为Intel(R) Core(TM)i5-4200U CPU,1.60G硬盘,4G RAM,操作系统为Windows 7 with SP1,编程软件为Visual Studio 2010 C++,OpenCV库。
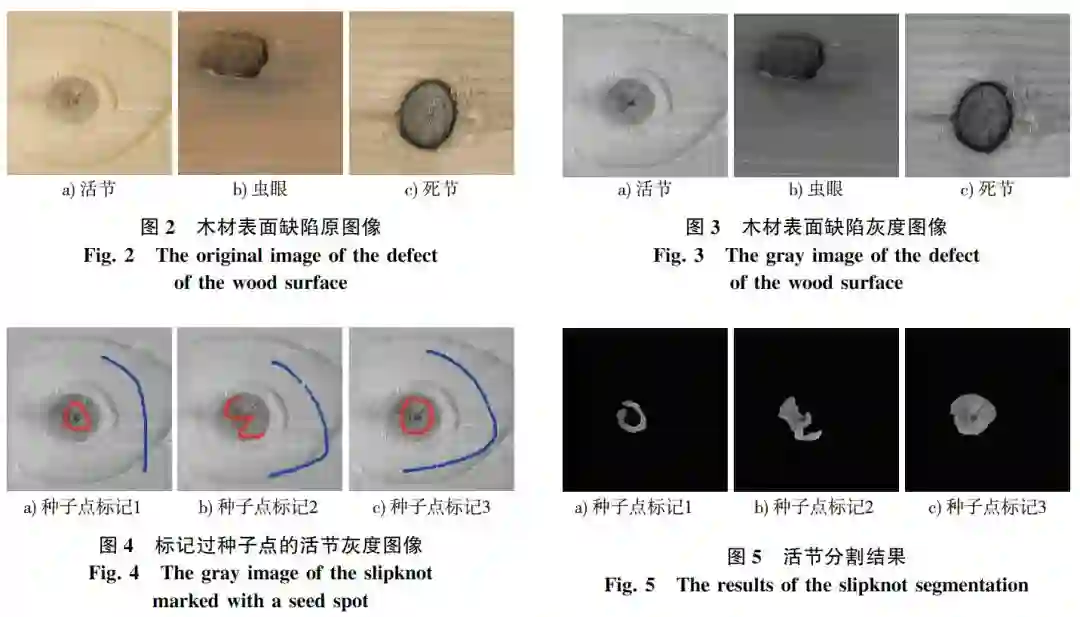
采用Graph Cuts算法对单缺陷目标图像进行图像分割,木材样本如图2,灰度图像如图3。
2.1.1 活节缺陷的图像分割
采用Graph Cuts算法对图3a活节缺陷图像进行分割,参数λ=1。试验中对活节灰度图像进行3次人工种子点标记(其中红色为目标标记,蓝色为背景标记,且标记画笔的半径是5个像素),如图4所示,对应的分割结果如图5所示。
Graph Cuts 算法是基于像素级的分割,不能准确评估像素属于前景或者背景的概率,由于活节缺陷边缘与背景的灰度值差距较小,即使标定的目标种子点像素数量很多(如图4c),但仍存在较严重的欠分割情况。对应图4a、b、c的分割初始化时间分别为41140.06,41022.37和40904.52ms,图像分割所用时间分别为146268.57,278338.17和388243.09ms。可见,种子点素数越多,初始化所用的时间越短,图像分割所用的时间越长。
2.1.2 虫眼缺陷的图像分割
采用同样的方法对图3b的虫眼缺陷图像进行分割:设置λ=1,3次人工标记种子点的结果如图6,对应的分割结果如图7。由试验结果可知,虫眼缺陷图像的分割结果与活节缺陷分割相似,分割结果受标定的前景/背景种子点像素数量影响,且都存在一定的欠分割问题。对应图7a、b、c的分割初始化时间分别为41152.20,41038.55和40894.37ms,图像分割时间分别为177052.53,368657.00和417434.91ms。种子点素数越多,初始化所用的时间越短,图像分割所用的时间越长。
2.1.3 死节缺陷的图像分割
对图3c死节缺陷图像进行分割:设λ=1,3次人工标记种子点的结果如图8,对应的分割结果如图9。可见,采用Graph Cuts算法对标注像素点多的死节缺陷图像能够实现完整分割,但死节缺陷的分割轮廓曲线不平滑,且存在部分过分割情况。对应图8a、b、c的初始化时间分别为40933.91,40921.05和40916.92ms,图像分割所用时间分别为34677.35,371604.00和413967.44ms。
综上所述,采用Graph Cuts算法对木材表面缺陷图像进行分割时,由于Graph Cuts算法对能量函数采用一次性最小化,对目标和背景的人工标记的种子点选取十分重要,选取结果直接影响分割结果;且该算法对相邻像素间的区分度较差,对活节和虫眼缺陷进行分割时存在欠分割问题,对死节缺陷进行分割时出现过分割情况。该算法的初始化时间随种子点标记的像素数的增加而缩短,运行时间相反。
2.2 基于Grab Cut算法的木材表面缺陷图像分割
采用Grab Cut算法对含有单缺陷目标、多缺陷目标的木材表面缺陷图像进行分割试验。试验的参数设定为距离参数β=0.1和GMM更新迭代次数k=5。木材缺陷图像为512×512的彩色图像。在试验过程中,首先输入相同的初始化矩形框。
2.2.1 单缺陷目标的图像分割
1)单活节图像分割:图10a为单个活节样本的原图像,图10b为初始化矩形框,图10d为分割结果,图10c为分割结果的局部放大图,图10e为分割结果与原图像的掩模。虽然活节缺陷的像素灰度值与背景的灰度值的差距较小,但Grab Cut算法仍然可以得到完整的分割轮廓, 分割时间为108144.784ms。由图10e可见,分割结果与原图的吻合度较高,分割效果较好;从图10c分割结果局部放大图可见,Grab Cut算法进行图像分割时,会使活节缺陷内部出现零星的欠分割区域。
2)单虫眼图像分割:图11a为单虫眼样本的原图像,图11b为初始化矩形框,图11d为分割结果,图11c为分割结果的局部放大图,图11e为分割结果与原图像的掩模。虽然活节缺陷的像素灰度值与背景的灰度值的差距较小,但Grab Cut算法仍然可以得到完整的分割轮廓, 分割时间为87329.92ms。由图11e可见,分割结果与原图的吻合度较高,分割效果较好;从图11c分割结果局部放大图可见,Grab Cut算法进行图像分割时,会使虫眼缺陷内部出现零星的欠分割区域。
3)单死节图像分割:图12a为单虫眼样本的原图像,图12b为初始化矩形框,图12d为分割结果,图12c为分割结果的局部放大图,图12e为分割结果与原图像的掩模。虽然活节缺陷的像素灰度值与背景的灰度值的差距较小,但Grab Cut算法仍然可以得到完整的分割轮廓, 分割时间为77545.63ms。由图12e可见,分割结果与原图的吻合度较高,分割效果较好;从图12c分割结果局部放大图可见,Grab Cut算法进行图像分割时,会使虫眼缺陷内部出现零星的欠分割区域。
综上所述,Grab Cut算法进行木材表面缺陷分割,能够得到完整的分割轮廓,且不受背景噪声影响,分割速度快,且对目标与背景像素差别较大的死节和虫眼缺陷分割速度更快,但分割结果均会出现少量的欠分割问题。
2.2.2 多缺陷目标的图像分割
1)多活节缺陷分割试验(图13):图13a为多活节样本的原图像,图13b为初始化矩形框,图13c为分割结果,图13d为分割结果与原图像的掩模。可见,Grab Cut算法能将木材表面的每一个活节缺陷都分割出来,且分割轮廓曲线完整,分割结果与原图的吻合度较高,但在背景中识别出两个过分割噪点,分割时间为13.337s。
2)多虫眼缺陷分割试验(图14):由图14可见,Grab Cut算法能将木材表面的每一个虫眼缺陷都分割出来,且分割轮廓曲线完整,分割效果好,分割结果与原图吻合度较高,分割时间为10.913s。
3) 多死节缺陷分割试验(图15):由图15可见,
Grab Cut算法能将木材表面的每一个死节缺陷都分割出来,且分割轮廓曲线完整,但是右下角死节缺陷的轮廓上存在少量过分割噪点,分割时间为11.634s。
由图13、14、15的分割结果可知,Grab Cut算法能够快速锁定多个木材表面缺陷的边界轮廓,且不受木材表面缺陷的多少、大小和缺陷轮廓形状的影响,分割效果好,分割速度快,抗噪性强,运行时间短。但是Grab Cut算法对木材表面缺陷分割时会出现零星的欠分割或者过分割情况,且分割前需要用户人工画定初始化矩形框。
来自:林业工程学报
-加入人工智能学院系统学习-
点击“阅读原文”进入学习