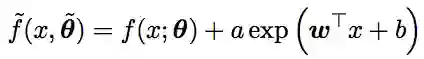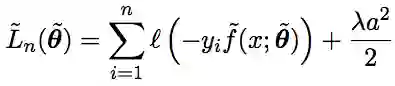用一个神经元破解不良的局部最小值问题

来源：arXiv

编译：Bing

编者按：深度学习的核心问题就是非常难的优化问题，在神经网络发展的几十年间，深度神经网络的优化问题的困难性是阻碍它们成为主流的主要原因。大部分传统机器学习问题是凸问题，即顺着梯度走到底就一定是最优解。然而深度学习以及小部分机器学习问题都是非凸的，所以在优化过程中可能会存在很多局部极小值点。在本篇论文中，美国伊利诺伊大学的研究者提出了一种方法，添加一个神经元就能破解不良局部极小值的问题。以下是论智的编译。

分析神经网络最主要的困难是损失函数的非凸性，这可能会导致许多不良的局部最小值。在这篇论文中，我们研究了用于二元分类任务的神经网络的结构。最终我们证明了在输出上或每一层都添加一个加入了skip connection的神经元后，每个局部最小值就成为了一个全局最小值。

论文摘要

深度神经网络最近在许多机器学习任务中获得了巨大的成功。然而，始终没有对神经网络理论上的解释。其中的一个难题就是在分析神经网络时，损失函数的非凸性会造成许多局部最小值的出现，这会让损失更大。长期以来这都被看作是神经网络的瓶颈，这也是为什么人们更喜欢支持向量机这类的公式。鉴于最近深度神经网络的成功，我们提出了一个有趣的问题，即神经网络的非凸性该怎么解决。

很多人猜想，所有经验损失的局部最小值能达到相似的训练效果。例如，之前的研究证明，结构相同但起始点不同的神经网络能收敛到的局部最小值表现出相似的分类性能。从理论上讲，最近许多研究都分析了神经网络损失函数的结构了。一些成果还研究了深度网络，但是它们要么需要用到线性激活函数，要么需要例如ReLU激活的独立性和过度参数化这样的假设。除此之外，许多研究都在探究单一隐藏层的神经网络，并提出许多能够让局部搜索算法找到全局最小值的条件。注意，即使对单层网络来说，在现有研究中通常也需要一些强有力的设定，例如过度参数化、特殊神经元的激活函数、固定第二层参数（或高斯数据分布）等。目前一些强大的设定反映了问题的难度：即使对单一隐藏层非线性神经网络来说，想要分析整体结构也是很难的，所以做出多种假设是合理的。

除了强大的假设，目前许多工作的结论并没有应用到所有的局部最小值中。其中一个典型结论是关于局部几何的（local geometry）。即，在全局最小值的小范围内，没有不良局部最小值的存在。另一个典型结论是：局部最小值的子集是全局最小值。这表示第二位的局部最小值的自己可以有和线性预测器一样的性能。现有的这几种结论反映出问题的复杂性：尽管分析全局结构看起来比较困难，我们也许可以退而求其次，分析局部结构或者是结构的主要部分。基于上述讨论，理想中的理论结果就是，在数据集、神经结构和损失函数的假设下，每个局部最小值都是全局最小值。

我们的成果

有了对背景的了解，我们主要的成果非常令人惊讶：在二元分类问题上，通过对神经网络结构的细微调整，每个局部最小值都是损失函数的全局最大值。我们的方法不需要提前对网络尺寸或者原始网络的种类进行限制，要点是在其中加入一个特殊的神经元（带有skip connection），同时还有与之相关的正则化项。

我们对损失函数和数据集做出了两个假设。在损失函数上，假设损失函数l(z)的每个重要的点都是全局最小是，每个全局最小值z满足z＜0。同时假设有一套参数θ ，神经网络f(1;θ )能够正确分辨数据集D中的所有样本。

两个假设

给定神经网络结构f(1;θ )，将其定义在一个d维的欧几里得空间中，同时有一套参数θ，我们在输出中添加一个指数神经元，定义一个新结构f^，即

这里向量θ^=（θ,a,w,b)表示神经网络f^的参数。对于这个新模型，我们定义实际损失函数为：

这里的标量λ是一个正实数，即λ＞0。与损失函数L_n不同，这里的损失函数L^_n在参数a上有一个正则化项，因为我们的目的是清除f^的输出上的指数神经元带来的影响。

我们主要的成果和应用具体有以下三点：

• 我们主要关注带有光滑hinge损失函数的二元分类问题。我们证明了：对任意神经网络来说，通过向网络中加入特殊的神经元（例如指数神经元），同时添加该神经元的二次正则化器，新的损失函数没有不良的局部最小值，并且每个局部最小值的错误分类误差都保持在最低水平。

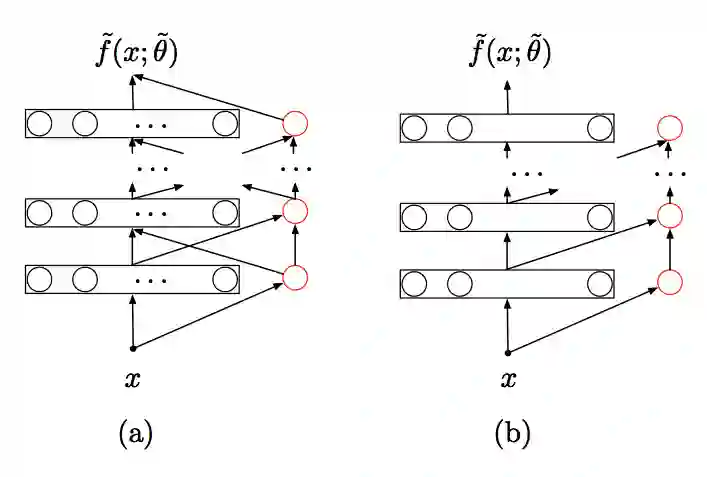
• 在主要的结论中，增强神经元可以看做是从输入到输出层的skip connection。然而，这个skip connection并不重要，因为如果我们添加一个特殊的神经元到完全连接的前馈神经网络中的每一层时，结果还是一样的。

• 据我们所知，这是深度非线性网络中第一个没有不良局部最小值的结果。我们的结果证明，“良好的神经网络”的种类包含了任何具有一个特殊神经元的网络，因此这个类别在所有神经网络种类中非常“密集”：任何一个神经网络想要变成良好神经网络，只差一个神经元而已。

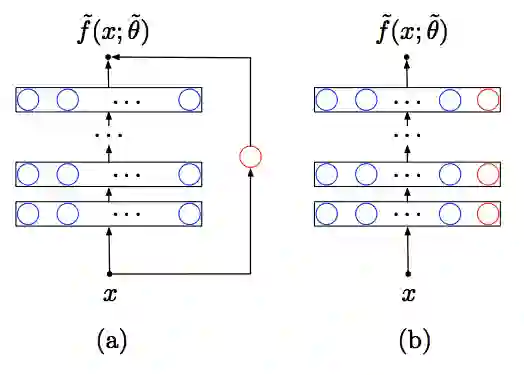
蓝色圆圈代表原始网络中的神经元，红色圆圈代表增强的指数神经元

（a）代表神经网络结构，（b）代表在任意局部最小值时的网络结构，这里所有指数神经元对神经网络最后的输出没有贡献。黑色圆圈代表原始网络中神经元的活动，红色圆圈代表指数神经元

结语

在这篇论文中，我们证明了任何一个神经网络，通过添加一个特殊的神经元和相关的正则化项，新的损失函数就没有不良的局部最小值。不仅如此，我们还证明了在新的损失函数中的每个局部最小值上，指数神经元是不活跃的，这意味着增强神经元和正则化项改进了损失的结构，没有影响原始神经网络的表现能力。我们还用几种方法扩展了主要结果。首先，当向神经网络中添加特殊神经元后，该神经网络与传统网络有了区别，同样的，在每个图层中添加一个特殊神经元都有这种效果。其次，如果我们将指数神经元变成对数据有依赖的多项式神经元，结果也是一样。最后，即使一个特征向量对应两个标签，结果仍然相同。

论文地址：arxiv.org/abs/1805.08671