2021图机器学习有哪些新突破？麦吉尔大学博士后一文梳理展望领域趋势

会员服务 ·

2021图机器学习有哪些新突破？麦吉尔大学博士后一文梳理展望领域趋势

2021 年 12 月 30 日 专知

选自Medium

作者：Michael Galkin

转载机器之心

图机器学习领域的热门趋势和重大进展。

又一年又接近尾声，还有三天我们就要告别 2021 年了。

各个 AI 领域也迎来了年度总结和未来展望，今天来讲一讲 AI 圈始终大热的图机器学习（Graph ML）。

2021 年，图机器学习领域涌现出了成千上万篇论文，还举办了大量的学术会议和研讨会，出现了一些重大的进展。2022 年，图机器学习领域又会在哪些方面发力呢

Mila 和麦吉尔大学博士后研究员、专注于知识图谱和图神经网络（GNN）研究的学者 Michael Galkin 在一篇博客中阐述了他的观点。在文中，作者对图机器学习展开了结构化分析，并重点介绍了该领域的主要进展和热门趋势。作者希望本文可以成为图机器学习领域研究者的很好的参考。

本图由 ruDALL-E 生成。

作者主要从以下 12 个部分进行了详细的梳理：

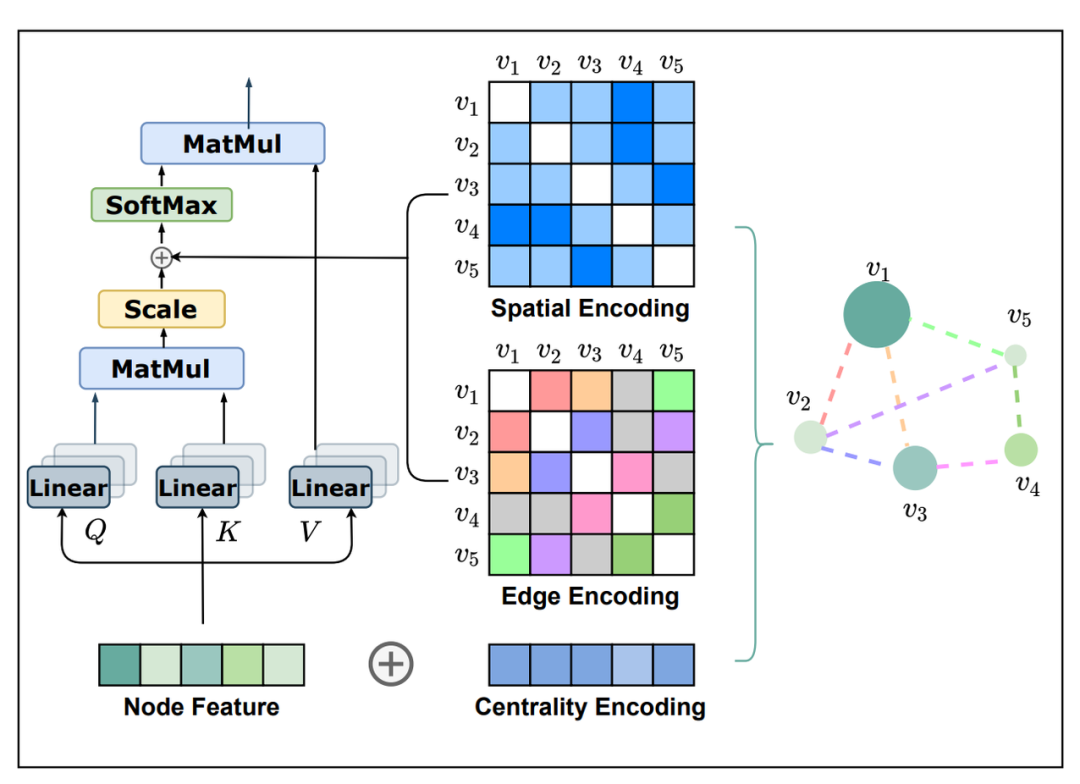
图 Transformers + 位置特征
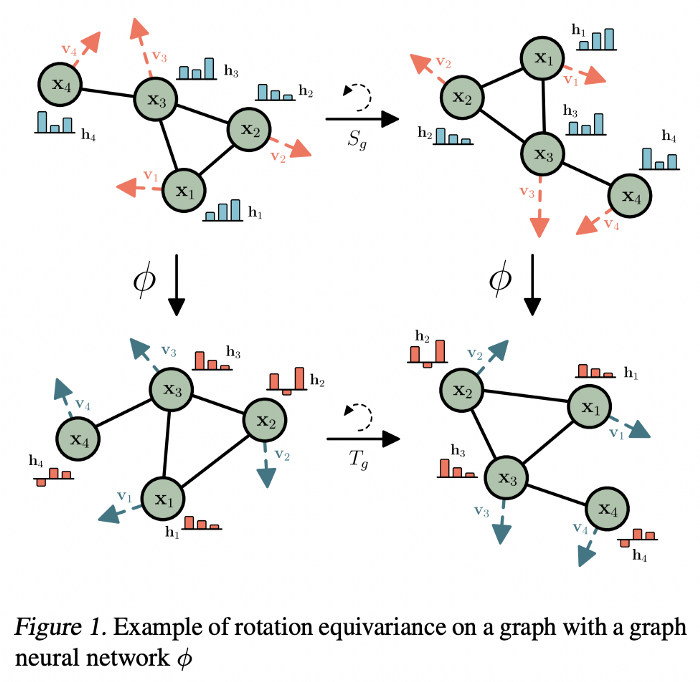
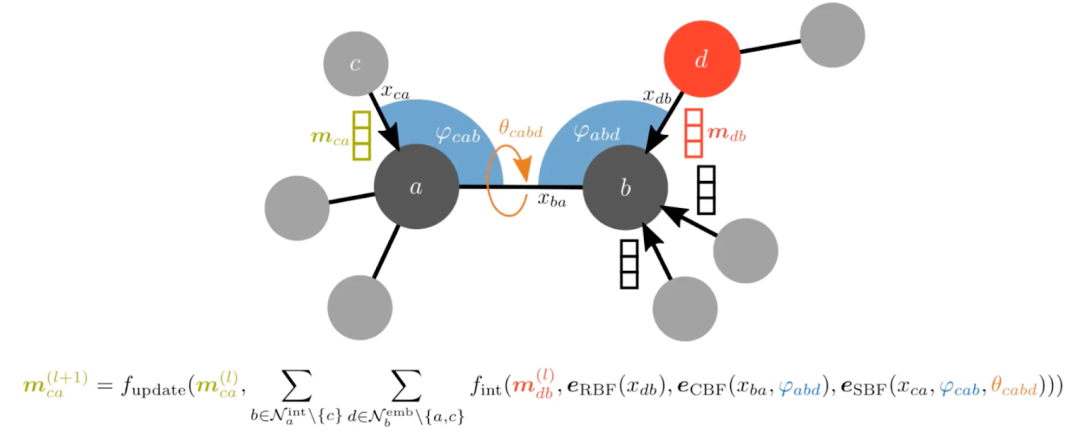
等变 GNNs
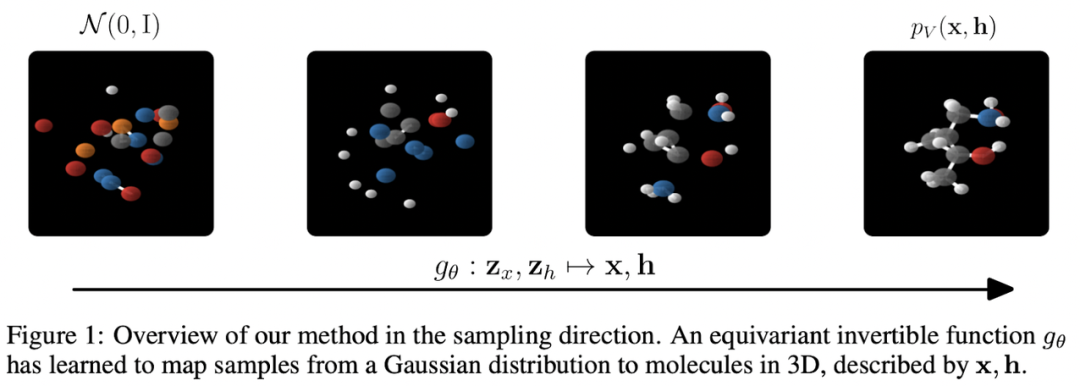
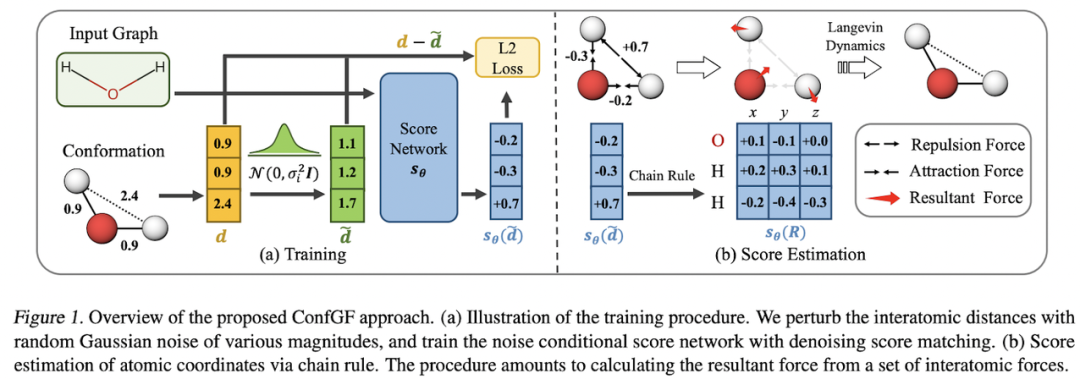
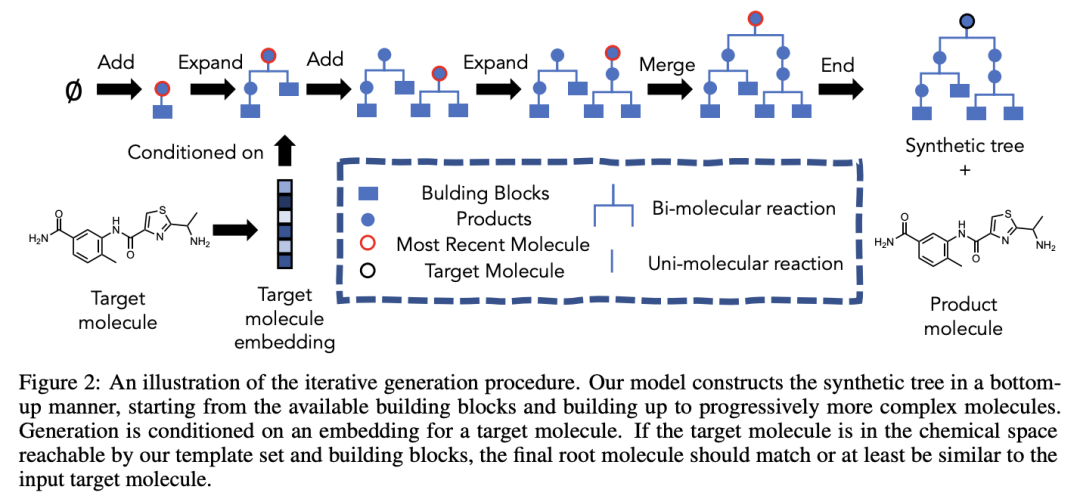
分子的生成模型
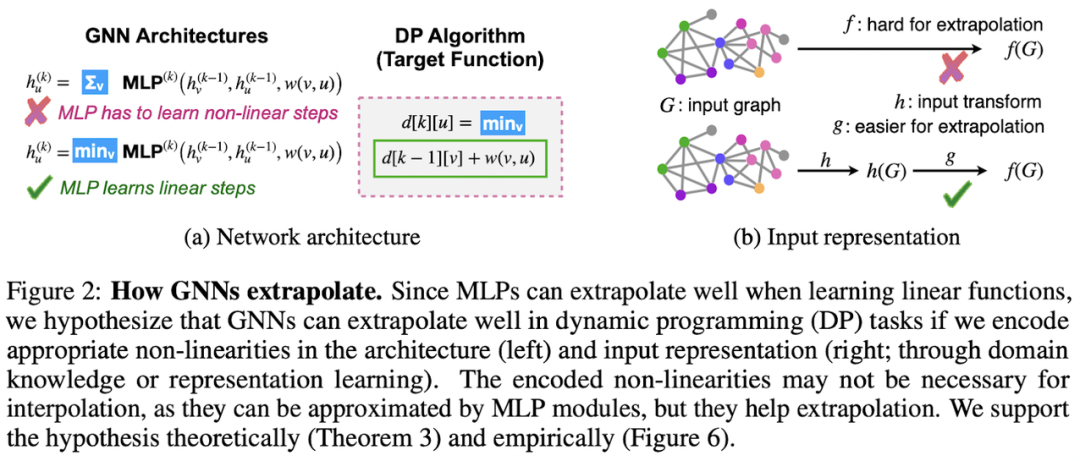
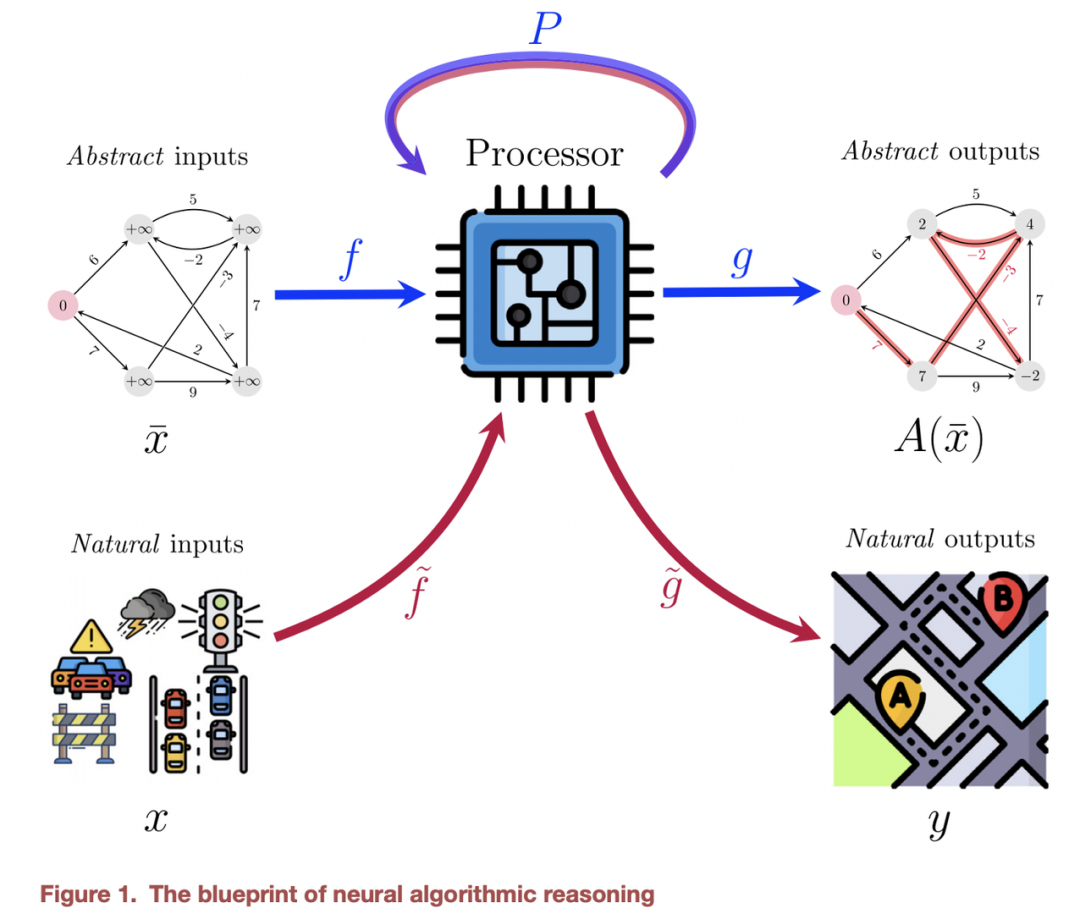
GNNs + 组合优化 & 算法
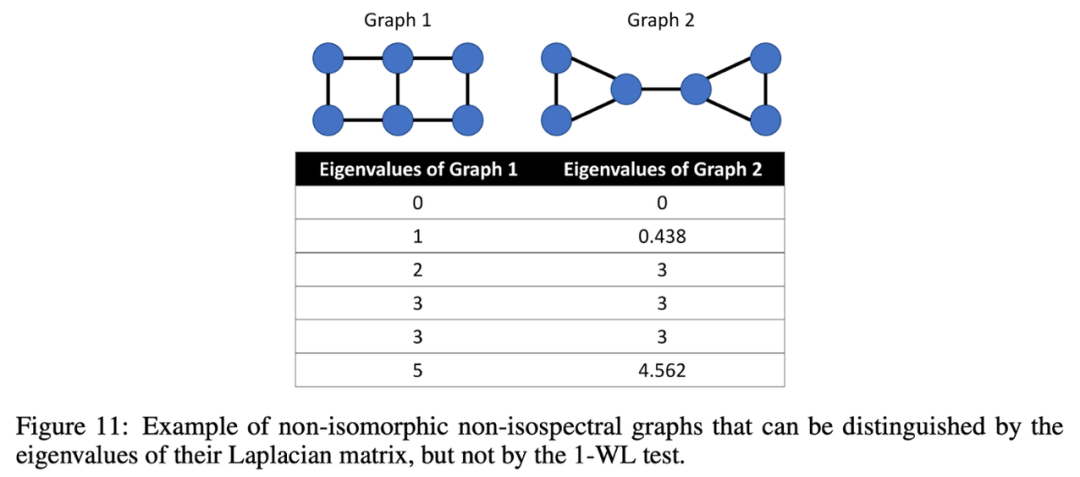
子图 GNN：超越 1-WL
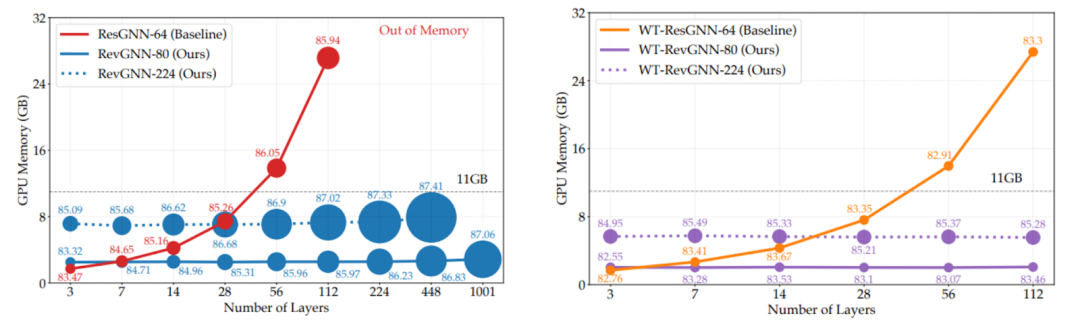
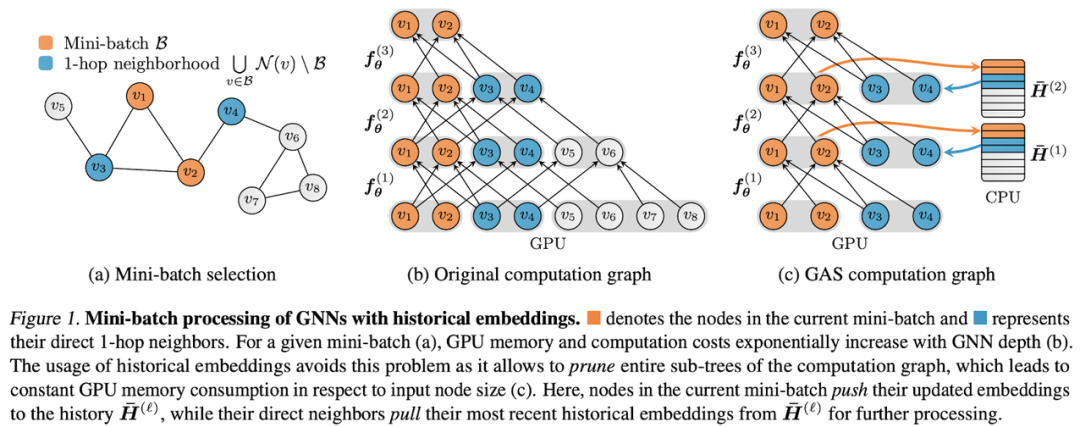
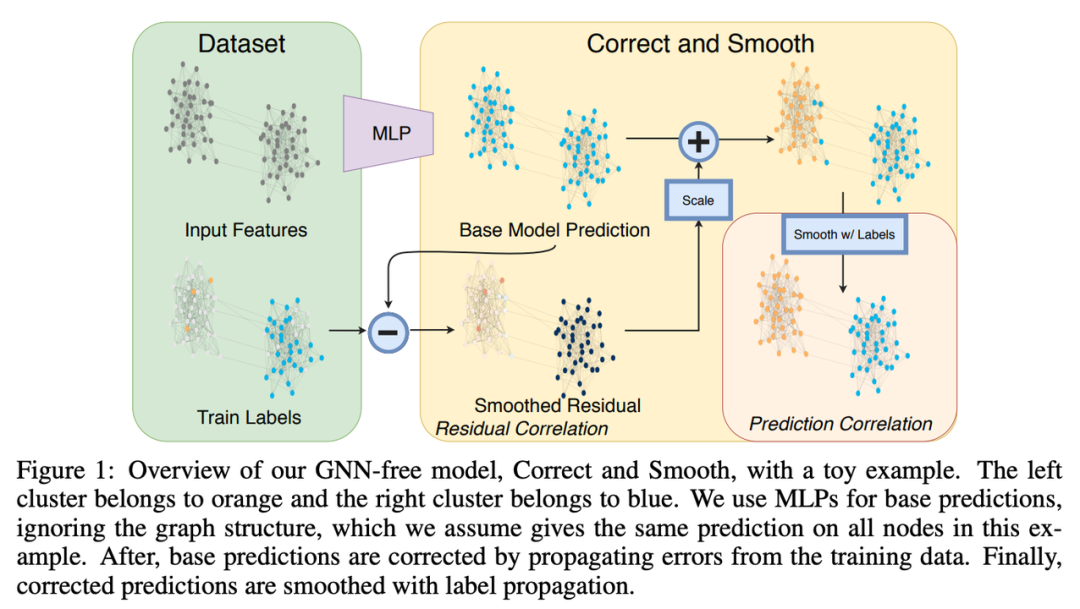
可扩展和深度 GNN：层数 100 及以上
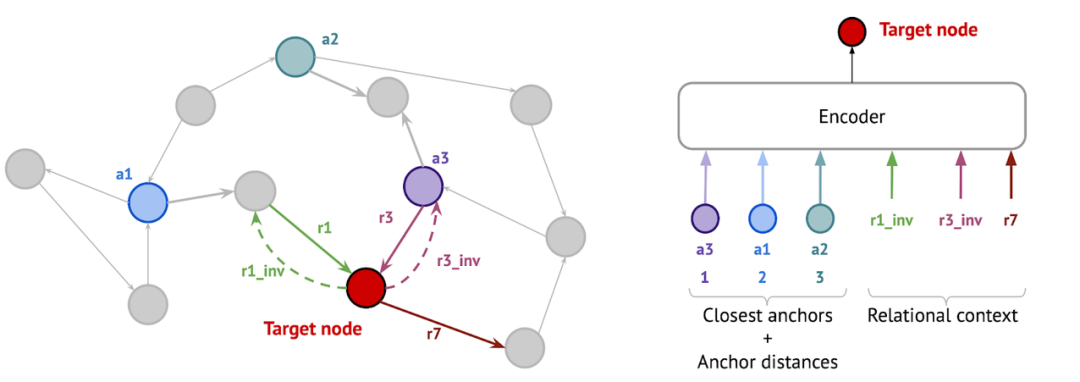
知识图谱
利用 GNN 做很酷的研究
新的数据集、挑战和任务
课程和书籍
库和开源
如何保持更新

图 Transformers + 位置特征

GNN 在（通常是稀疏的）图上运行，而 Graph Transformers (GT) 在全连接图上运行，其中每个节点都连接到图的其他节点。一方面，在节点数为 N 的图中，图的复杂度为 O(N^2) 。另一方面，GT 不会过度平滑，这是长程消息传递的常见问题。全连接图意味着你有来自原始图的真边和从全连接变换添加的假边，你需要进行区分。更重要的是，你需要一种方法来为节点注入一些位置特征，否则 GT 不会超过 GNN。

今年最流行的两个图 transformer 模型为 SAN 和 Graphormer。Kreuzer、Beaini 等人提出的 SAN 采用拉普拉斯算子的 top-k 特征值和特征向量。SAN 将光谱特征与输入节点特征连接起来，在许多分子任务上优于稀疏 GNN。

Ying 等人提出的 Graphormer 采用空间特征。首先，节点特征丰富了中心编码；然后，注意力机制有两个偏置项：节点 i 和节点 j 之间的最短路径距离；依赖于一条可用最短路径的边缘特征编码。

Graphormer 实现了 2021 年 Graph ML 大满贯：OGB large Challenge 和 Open Catalyst Challenge 夺得冠军

等变 GNN

等方差有何独特之处，让 Geoffrey Hinton 如此赞美？

一般来说，等方差被定义在某些转换组上，例如，3D 旋转形成 SO(3) 组，特殊正交以 3D 的形式组合。等变模型在 2021 年掀起了 ML 的风暴，在图机器学习中的许多分子任务中尤其具有突破性。应用于分子时，等变 GNN 需要一个额外的节点特征输入，即分子物理坐标的一些表征，这些表征将在 n 维空间中旋转 / 反射 / 平移。

在等变模型中，尽管变换的顺序不同，但我们都能到达相同的最终状态。图源：Satorras, Hoogeboom, and Welling

Satorras、Hoogeboom 和 Welling 提出了 EGNN、E(n) 等变 GNN，其与普通 GNN 的重要区别在于向消息传递和更新步骤添加物理坐标。等式 3 将相对平方距离与消息 m 相加，等式 4 更新位置特征。EGNN 在建模 n 体（n-body 系统、作为自动编码器和量子化学任务（QM9 数据集）方面显示出令人印象深刻的结果。

与 vanilla GNN 的主要区别：等式 3 和 4 将物理坐标添加到消息传递和更新步骤中。图源：Satorras, Hoogeboom, and Welling

另一种选择是合并原子之间的角度，就像 Klicpera、Becker 和 Günnemann 在 GemNet 中所做的那样。这可能需要将输入图转换为折线图，例如边图，其中来自原始图的边变成折线图中的节点。这样，我们就可以将角度作为新图中的边缘特征。

GemNet 在包括 COLL、MD17 和 Open Catalyst20 分子动力学任务上取得了不错的成绩，显然，等变 GNN 才刚刚起步，我们将在 2022 年看到更多进步！

分子的生成模型

由于几何深度学习，整个药物发现领域在 2021 年实现了大幅的跃进。药物发现的众多关键挑战之一是生成具有所需属性的分子（图）。这个领域很广阔，这里只提到模型的三个分支。

归一化流

Satorras、Hoogeboom 等人应用上述等变框架创建了 E(n) 等变归一化流，能够生成具有位置和特征的 3D 分子。

Shi、Luo 等人研究了在给定 2D 图形的情况下生成 3D 构象异构体（即 3D 结构）的问题。模型 ConfGF 估计了原子坐标对数密度的梯度场。这些字段是旋转平移等变的，作者想出了一种方法将这种等变属性合并到估计器中。Conformer 采样本身是通过退火朗之万动力学采样完成的。

RL 方法

该方法是以一种非常非科学的方式描述的，这些方法通过逐步附加「构建模块」来生成分子。可以根据这些方法对构建过程的调节方式对其进行广义分类。

例如，Gao、Mercado 、 Coley 以可合成性为构建过程的条件，即是否可以在实验室中实际创建这种分子。为此，他们首先学习了如何创建构建块的合成树（一种模板）。

Yoshua Bengio 领导的 Mila 和斯坦福团队提出了一个更通用的框架，他们引入了生成流网络（GFlowNets）。这很难用几句话来概括：首先，当我们想要对不同的候选者进行采样时，GFlowNets 可以用于主动学习案例，并且采样概率与奖励函数成正比。此外，团队最近的 NeurIPS'21 论文展示了 GFlowNets 应用于分子生成任务的用处。Emmanuel Bengio 的博客文章更详细地描述了该框架并提供了更多的实验证据：http://folinoid.com/w/gflownet/

GNNs + 组合优化 & 算法

2021 年，对于这个新兴的子领域来说是重要的一年。

Xu et al 在 ICLR’21 的论文中研究了神经网络的外推，并得出了一些亮眼的结论。基于算法对齐的概念，作者表示，GNN 与动态规划（DP）可以很好地对齐（如下图所示）。事实上，将经典 Bellman-Ford 算法寻找最短路径的迭代和通过 GNN 的信息的聚合组合步骤做比较，会发现很多共同点。

此外，作者表明，在建模特定 DP 算法时，为 GNN 选择合适的聚合函数至关重要，例如，对于 Bellman-Ford，需要一个最小聚合器（min-aggregator）。作者 Stefanie Jegelka 在 2021 年深度学习和组合优化研讨会上细致讲述了这项工作的主要成果：https://www.youtube.com/watch?v=N67CAjI3Axw

为了更全面的介绍这个领域，还需要重点介绍 Cappart et al 在 IJCAI’21 上的一项研究，该调查涵盖了 GNN 中的组合优化。这篇文章首次出现了神经算法推理蓝图，后来 Veličković 和 Blundell 的 Patterns 中的立场文件也对此进行了描述。

这个蓝图解释了神经网络如何在嵌入空间中模仿和授权一般离散算法的执行过程。在编码 - 处理 - 解码方式中，抽象输入（从自然输入获得）由神经网络（处理器）进行处理，其输出被解码为抽象输出，然后可以映射到更自然的任务特定输出。

例如，如果抽象输入和输出可以表示为图形，那么 GNN 可以即可成为处理器网络。离散算法的一个常见的预处理步骤是将我们对这个问题的任何所知内容转化为像「距离」或「边缘容量」这样的标量，并在这些标量上运行算法。相反，向量表征和神经执行可以轻松启用高维输入而不是简单的标量，并附加反向传播以优化处理器。

目前，该蓝图已经得到越来越多的采用，NeurIPS'21 上出现了一些很酷的作品。Xhonneux et al 研究了迁移学习是否可用于将学习到的神经执行器泛化到新任务；Deac et al 发现了强化学习中算法推理和隐式规划之间的联系。相信在 2022 年还会出现更多有关研究。

子图 GNN：超越 1-WL

如果 2020 年是首次尝试离开 GNN 表现力的 1-WL-landia 的一年，那么 2021 年则是超越 1WL-landia 的一年。这些联系已被证明很有用，我们现在拥有一些强大且更具表现力的 GNN 架构，这些架构将消息传递扩展到更高阶的结构，如单纯复形（例如 Bodnar、Frasca、Wang 等人的 MPSN 网络、胞腔复形（Bodnar、Frasca 等人的 CW Networks ））或子图。

可扩展性和深度 GNN

如果你在使用 2-4 层 GNN 时羡慕深度 ResNet 或 100 多层的大型 Transformer，那么 2021 年有两篇论文为我们带来了福音，一篇是关于随意训练 100-1000 层 GNN 的论文，另一篇是关于几乎恒定大小的邻域采样。

Li 等人提出了两种新机制，可以在训练极深的超参数化网络时减少 GPU 内存消耗：将 L 层网络的 O(L) 降低到 O(1)。作者展示了如何在 CV 或高效 Transformer 架构（例如 Reformer）中使用可逆层，并在层之间共享权重（权重绑定），以训练多达 1000 层的 GNN。下图展示了根据 GPU 需求进行的层数扩展。

图源：Li 等人的论文《 Training Graph Neural Networks with 1000 Layers 》

Godwin 等人提出了一种利用循环学习深度 GNN 的方法——在块（Block）中组织消息传递步骤，每个块可有 M 个消息传递层。然后循环应用 N 个块，这意味着有多个块共享权重。如果有 10 个消息传递层和 10 个块，你将得到一个 100 层的 GNN。其中一个重要的组成部分是 Noisy Nodes 正则化技术，它会干扰节点和边的特征并计算额外的去噪损失。该架构能更好地适用于分子任务，研究团队还在 QM9 和 OpenCatalyst20 数据集上进行了评估。

最后，如果想将任意 GNN 扩展成非常大的图，那么只有一个选择——采样子图。通常，对 k-hop 子图进行采样会导致指数级内存成本和计算图大小。

PyG 的作者 Matthias Fey 等人创建了一个在恒定时间内利用历史嵌入和图聚类扩展 GNN 的框架 GNNAutoScale。该方法在预处理期间将图划分为 B 个集群（小批量），以便最小化集群之间的连通性；然后在这些集群上运行消息传递与全批量设置一样好，并显著降低了内存要求（小了约 50 倍），这使得在商品级 GPU 上安装深度 GNN 和大型图成为可能。

知识图谱（KG）

在 2021 年之前，模型根据归纳偏置、架构和训练机制被明确分为转导和归纳两类。换句话说，转导模型没有机会适应未见过的实体，而归纳模型在中大型图上训练成本太高。2021 年有两种新架构在转导和归纳环境中均可使用。这两种架构不需要节点特征，可以在归纳模式中以与转导模式相同的方式进行训练，并可扩展到现实世界的 KG 大小。

一种是 Zhu 等人的神经 Bellman-Ford 网络，其中将经典的 Bellman-Ford 推广到了更高级别的框架，并展示了如何通过使用特定运算符实例化框架来获得其他经典方法（如 Katz 指标、PPR 、最宽路径等）。更重要的是，该研究表明泛化的 Bellman-Ford 本质上是一种关系 GNN 架构。NBFNet 不学习实体嵌入，这使得模型通过泛化到未见过的图而获得了归纳性。该模型在关系图和非关系图上的链接预测任务上都表现出色。在 KG 的应用上，NBFNet 给 FB15k-237 和 WN18RR 两个数据集带来了自 2019 年以来最大的性能提升，同时参数减少了 100 倍。

另一种是 Galkin 等人受 NLP 中标记化算法启发的新方法。在 KG 上应用时，NodePiece 将每个节点表征为一组 top-k 个最近的锚节点和节点周围的 m 个唯一关系类型。锚点和关系类型被编码为可用于任何下游任务（分类、链接预测、关系预测等）和任何归纳 / 转导设置的节点表征。NodePiece 特征可以直接被 RotatE 等非参数解码器使用，也可以发送到 GNN 进行消息传递。该模型在归纳链接预测数据集上的性能可与 NBFNet 媲美，并在大型图上表现出较高的参数效率——OGB WikiKG 2 上的 NodePiece 模型所需参数仅为浅的仅转导模型的一百分之一。

利用 GNN 做很酷的研究

Huang, He 等人在 ICLR’21 上展示了 Correct & Smooth — 一个通过标签传播改进模型预测的简单程序。仅与 MLP 配对，该方法在不使用任何 GNN 且参数少得多的情况下以最高分冲击 OGB 排行榜！今天，几乎所有 OGB 节点分类赛道中的顶级模型都使用 Correct & Smooth 来压缩更多的点。

图源：Huang, He 等人

Knyazev 等人在前向传递中预测各种神经网络架构参数的工作震惊了 ML 社区。他们没有采用随机初始化模型，而是采用预测好的参数，这样会优于随机模型。

参数预测实际上是一个图学习任务——任何神经网络架构（ResNet、ViT、Transformers）都可以表示为一个计算图，其中节点是具有可学习参数的模块，节点特征是那些参数，网络有一堆节点类型（比如，线性层、卷积层等，作者使用了大约 15 种节点类型）。参数预测则是一个节点回归任务。计算图使用 GatedGNN 进行编码，并将其新表示发送到解码器模块。为了训练，作者收集了一个包含 1M 个架构（图）的新数据集。该方法适用于任何神经网络架构，甚至适用于其他 GNN。

预测未知模型的参数的 pipeline。图源：Knyazev 等人

DeepMind 和谷歌通过将道路网络建模为超分段图并在其上应用 GNN，极大地提高了谷歌地图中 ETA 的质量。在 Pinion 等人的论文中，该任务被定义为节点级和图级回归。除此之外，作者还描述了许多需要解决的工程挑战，以便在谷歌地图规模上部署系统。应用 GNN 解决数百万用户面临的实际问题。

论文地址：https://arxiv.org/pdf/2108.11482.pdf

图源: Pinion 等人

一些资料总结

文章最后，作者介绍了一些相关资料，包括数据集、课程和书籍、一些实用的库等内容。

如果你不习惯使用 Cora、Citeseer、Pubmed 数据集，可以考虑以下：

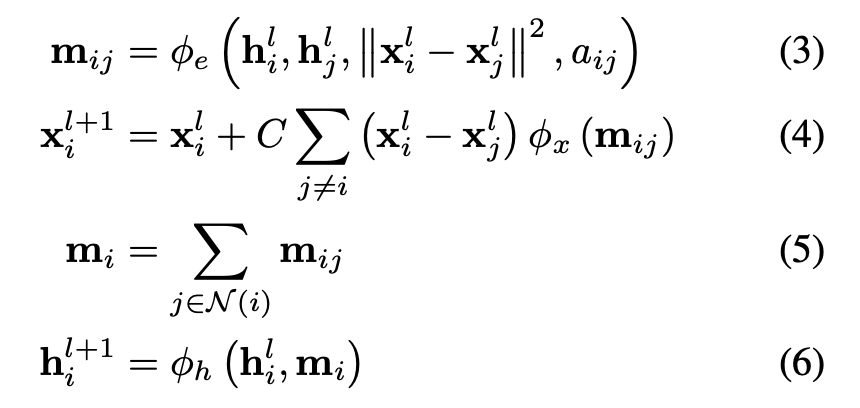
OGB 数据集包含 3 个非常大的图，可分别用于节点分类（240M 节点）、链接预测（整个 Wikidata，90M 节点）和图回归（4M 分子）任务。在 KDD Cup 中，大多数获胜团队使用了 10-20 个模型组合；
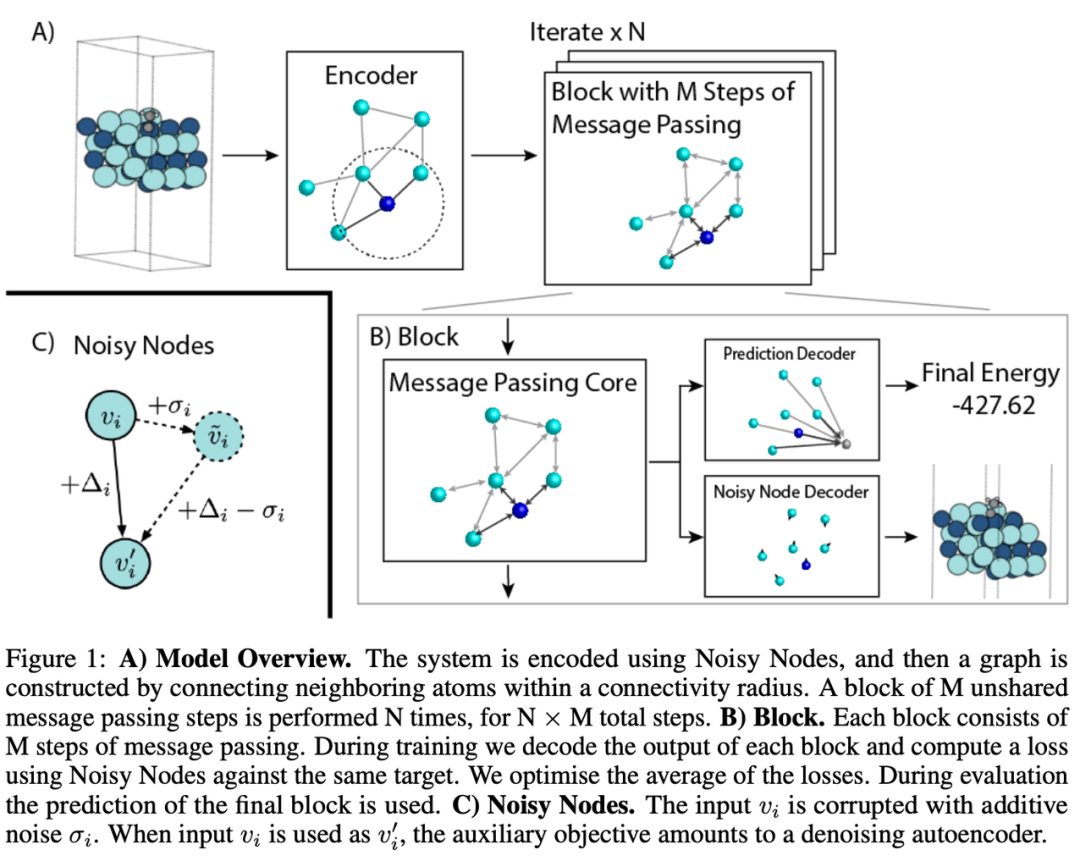
由 Meta AI 发起的公开催化剂挑战赛（ Open Catalyst NeurIPS’21 Challenge ），提供了一项大型分子任务——给出具有原子位置的初始结构，预测其松弛状态能。这个数据集非常庞大，需要大量的计算，但组织者暗示将发布一个更小的版本，这将对 GPU 预算有限的小型实验室更友好。事实上，Graphormer 在 OGB LSC 和 OpenCatalyst ' 21 中都获得了第一名，并在 2021 年获得了 Graph ML 的大满贯；
GLB 2021 带来了一组新的数据集，包括 Lim 等人提出的 non-homophilous graphs ，Tsitsulin 等人提出的 graph simulations，以及 Rozemberczki 等人提出的 spatiotemporal graphs 等；
NeurIPS’21 数据和基准赛道带来了新数据集，MalNet 可用于图分类，该数据集的平均图大小是 15k 节点以及 35k 边；ATOM3D 可用于 3D 分子任务；RadGraph 可用于从放射学报告中提取信息。

由 Michael Bronstein、Joan Bruna、Taco Cohen 和 Petar Veličković 编写的几何深度学习原型书和课程，包含 12 个讲座和实践教程和研讨会。