最新《深度卷积神经网络理论》报告，35页ppt

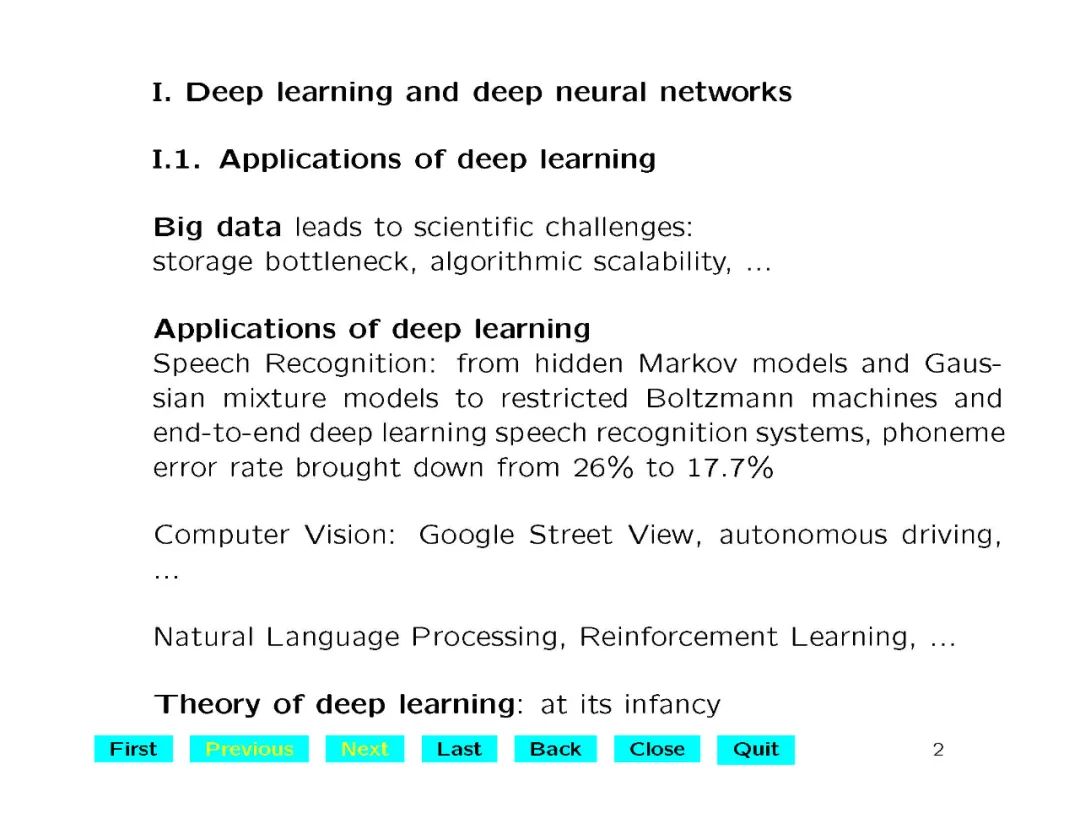
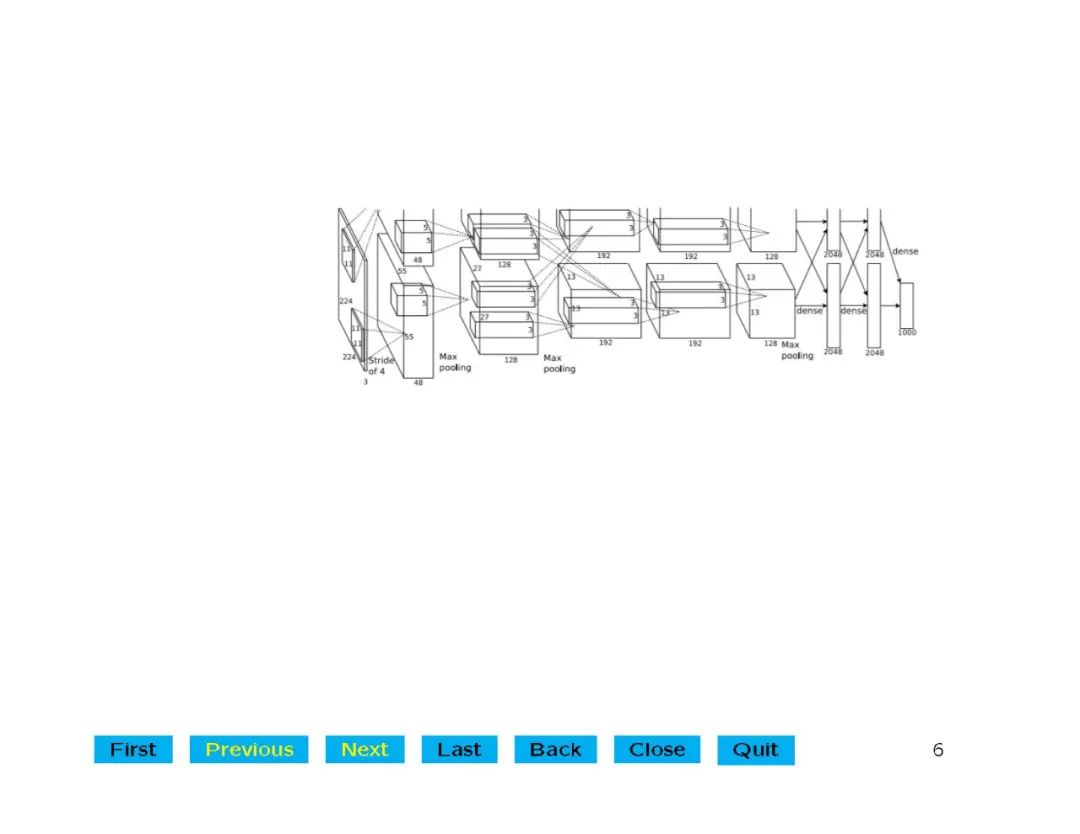
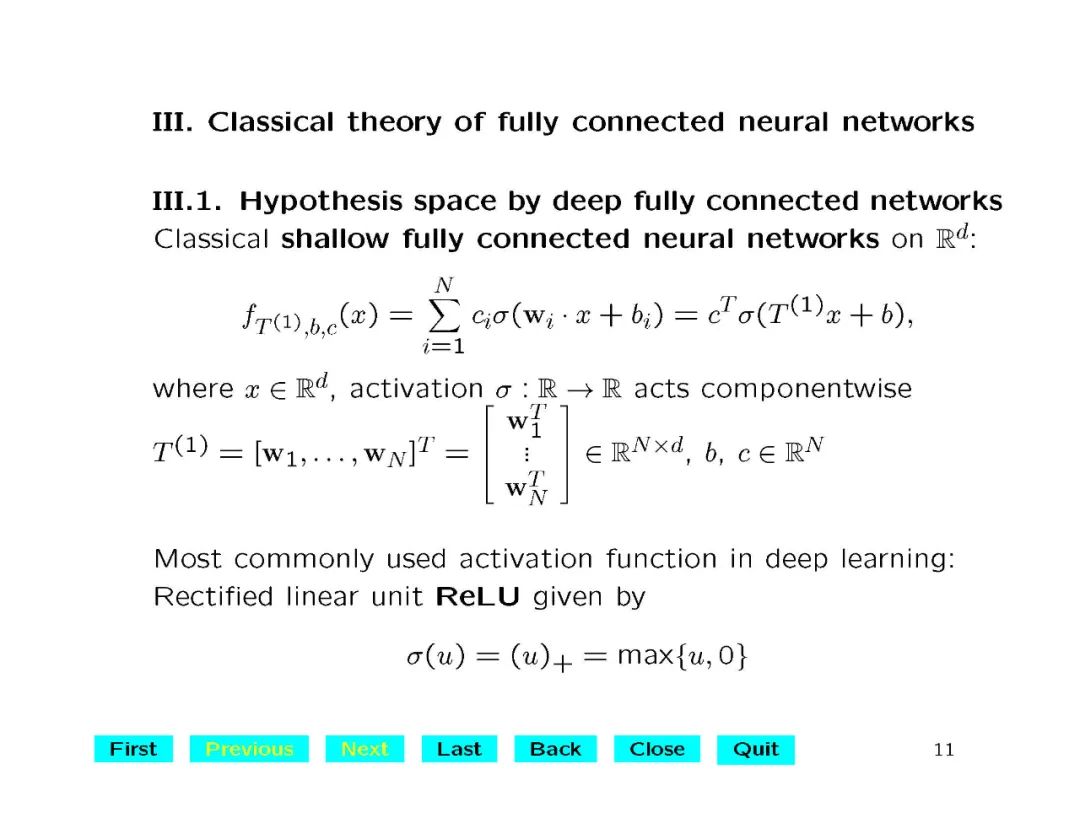
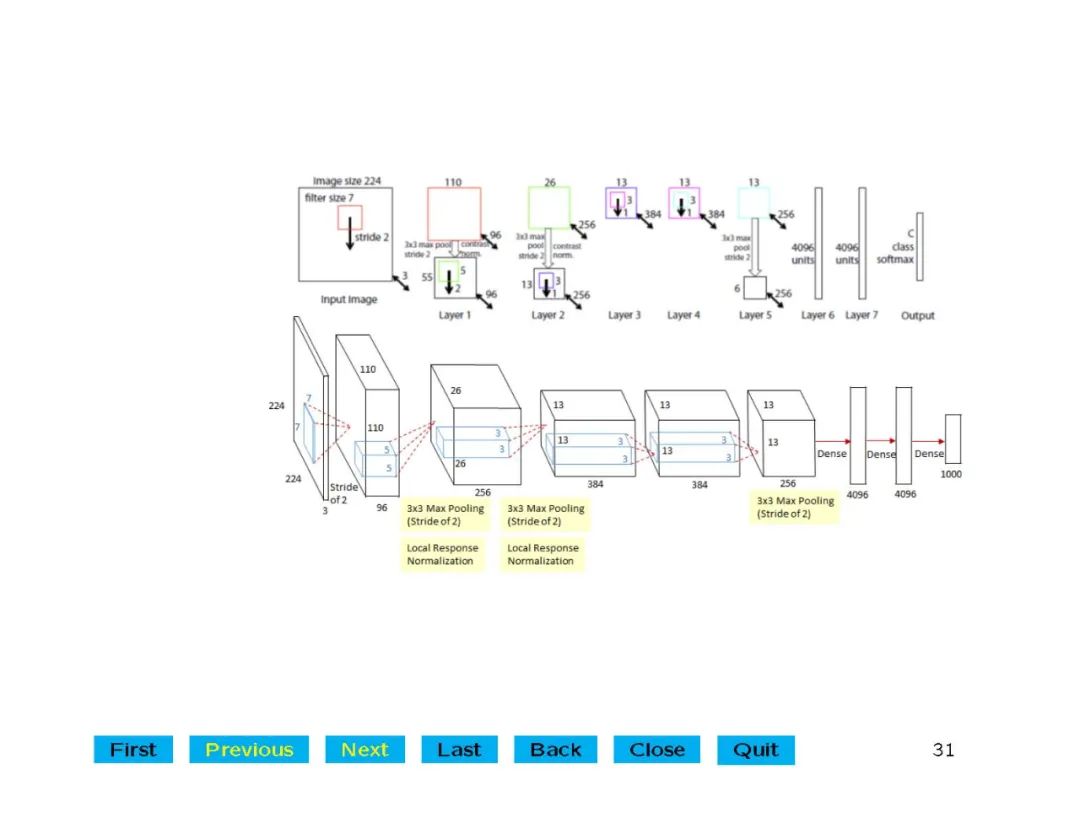
深度学习在语音识别、计算机视觉等许多领域得到了广泛的应用和突破。其中涉及的深度神经网络结构和计算问题已经在机器学习中得到了很好的研究。但对于理解深度学习模型在网络架构中的建模、逼近或泛化能力，缺乏理论基础。在这里，我们对具有卷积结构的深度卷积神经网络(CNNs)很感兴趣。convolutional architecture使得deep CNNs和fully connected deep neural networks有本质的区别，而30年前发展起来的关于fully connected networks的经典理论并不适用。本讲座介绍了深度神经网络的数学理论与整流线性单元(ReLU)激活函数。特别是，我们首次证明了深度CNN的普遍性，即当神经网络的深度足够大时，深度CNN可以用来逼近任意的连续函数，达到任意的精度。我们还给出了显式的逼近率，并表明对于一般函数，深度神经网络的逼近能力至少与全连接多层神经网络一样好，对于径向函数更好。我们的定量估计严格按照待计算的自由参数的数量给出，验证了深度网络神经网络处理大数据的效率。

https://github.com/deeplearning-math/deeplearning-math.github.io

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“CNNT” 就可以获取《最新《深度卷积神经网络理论》报告，35页ppt》专知下载链接

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源