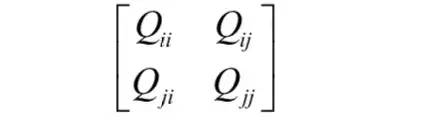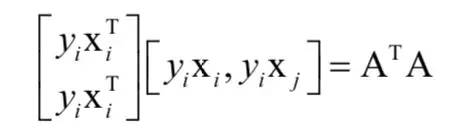免费赠书 | 首波圣诞福利：清华大牛手把手教你机器学习与实践

过了这个周末

圣诞节就来啦

为庆祝这个特别的节日

极市决定当一回圣诞老人

给 各 位 提 前 送 一 波 礼 物  啦！

机器学习和深度学习领域又一力作 ——《机器学习与应用》免费送！本书是毕业于清华大学计算机系的雷明大佬新书，系统、深入地讲述了机器学习与深度学习的主要方法与理论，并紧密结合工程实际与应用，值得入手。

❆

作者简介

雷明，毕业于清华大学计算机系，研究方向为机器学习、计算机视觉。有超过12年的学术研究与产品研发经验，曾发表论文数篇，具有深厚的理论功底与丰富的实践经验。其撰写的系列技术文章在半年内累计阅读量达数百万次，擅长用生动、形象的语言把复杂、抽象的理论和算法解释清楚。

❆

超级福利

本文已经同步发布在极市开发者社区（http://bbs.cvmart.net/articles/142，或直接阅读原文）即刻起只要在社区赠书推文帖下提出关于本书的疑问或留言回复机器学习深度学习中遇到的问题，极市将邀请本书作者雷明大大在社区中回复答疑。

大牛作者亲自与你交流技术问题

简直比圣诞老人还圣诞老人啊

机会难得不可错过哦~

如何参与：

前往 http://bbs.cvmart.net/articles/142 或直接阅读原文，留言提出关于本书的疑问或机器学习中遇到的问题，极市将邀请雷明大大在社区中回复答疑，12月24日18:00，极市和雷老师会在所有留言中随机抽选5位者免费赠送《机器学习与应用》纸质书籍一本。

更多福利：

所有留言回复者均可获得一份极市整理的技术干货资源（含CVPR/VALSE/PRCV论文及视频资源、电子书籍/学习资料等）

适读人群：

计算机，电子，自动化，人工智能等相关专业的本科生，研究生

从事人工智能学术研究与产品研发的人员

对人工智能、机器学习感兴趣的人

活动时间：即刻起至12月24日18:00

立即参与：http://bbs.cvmart.net/articles/142

❆

本书优势（附精彩试读）

1、内容全面、系统，紧跟时代步伐

完整的讲述了机器学习、深度学习主要算法以及在各个领域的典型应用，含括了学术界与工业界截止2017年初的新成果，紧跟时代步伐，弥补了市面上经典教材内容老化的缺憾。

精彩试读

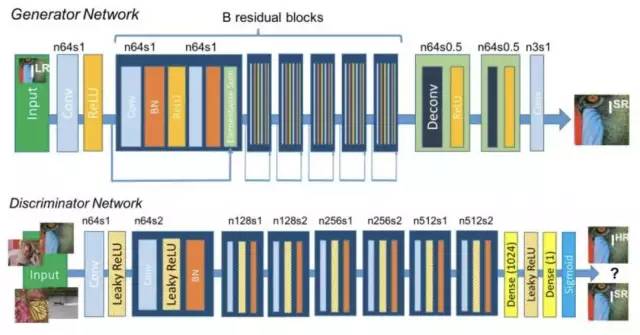
图像超分辨的目标是由低分辨率的图像得到高分辨率的图像，传统的做法大多采用纯图像处理的技术。用机器学习的思路解决超分辨问题取得了更好的效果，卷积神经网络被成功地用于超分辨问题。文献[7]提出了一种用生成对抗网络框架解决图像超分辨问题的方法，称为超分辨生成对抗网络，简称SRGAN，能够将缩小4倍以上的图像进行复原。

这种方法使用了一种新的损失函数，由对抗损失和内容损失两部分构成。第一部分损失和标准生成对抗框架相同，通过一个判别模型，让生成网络生成的超分辨图像和真实高分辨率图像尽可能接近。

生成器卷积网络采用了深度残差网络；判别模型也是一个层次很深的卷积网络，用于区分一张图像是真实的高分辨率图像还是由生成器网络生成的图像。网络结构如下图所示。

图像超分辨的网络结构

假设低分辨率图像为ILR，这里的目标是根据它估计出高分辨率的图像ISR，在训练样本中与低分辨率图像相对应的真实高分辨率图像为IHR。

2、推导论证清晰、深入、详细

绝大部分核心算法均有详细的推导、证明过程，从问题本源、思想层面对算法进行讲解，让读者不仅知其然还知其所以然，真正掌握算法的思想与精髓。在书的前部对机器学习所需的数学知识也做了系统的讲解

精彩试读

目标函数的二阶导数为η，前面假设二阶导数η>0，从而保证目标函数是凸函数，即开口向上的抛物线，有极小值。如果η<0，或者η=0该怎么处理？对于线性核或正定核函数，由于矩阵K的任意一个上述子问题对应的二阶子矩阵半正定，必定有η>=0。下面给出证明这个关于两个变量的子问题的目标函数是凸函数，只需要证明它的Hessian矩阵是半正定矩阵。这两个变量的目标函数的Hessian为

和10.3.2节证明整个对偶问题的Hessian矩阵正定的方法相同，如果是线性核，这个矩阵也可以写成一个矩阵和它的转置的乘积形式：

矩阵A为训练样本特征向量乘上类别标签形成的矩阵。显然这个Hessian矩阵是半正定的，因此必定有η>=0。如果是非线性核，因为核函数相当于对两个核映射之后的向量做内积，因此上面的结论同样成立。

无论本次迭代时αi和αj的初始值是多少，通过上面的子问题求解算法得到是在可行域里的最小值，因此每次求解更新这两个变量的值之后，都能保证目标函数值小于或者等于初始值，即函数值下降，所以SMO算法能保证收敛。

3、核心算法配有实现细节介绍，使用示例，知名开源库代码分析

对大部分核心算法的实现细节进行了介绍，并配有示例程序与知名开源库源代码分析，包括OpenCV，libsvm，liblinear，Caffe，这对需要使用、实现机器学习算法的读者至关重要。

精彩试读

求解器的实现是源代码分析的核心，分为可信域牛顿法与坐标下降法两类。可信域牛顿法由TRON类实现，坐标下降法由各个问题具体的求解函数实现。限于篇幅，在这里只分析一部分求解器，其他的实现原理类似。

可信域牛顿法由类TRON实现，这个类为L2-正则化logistic回归和L2-正则化支持向量机的训练提供支持。类定义如下：

class TRON

{

public:

       // 传入的是基类function的指针，可以使用上面两种损失函数，eps为迭代精度

       // max_iter为最大迭代次数，默认值为1000

       TRON(const function *fun_obj, double eps = 0.1, int max_iter = 1000);

       ~TRON();

       // 这是求解的接口函数

       void tron(double *w);

       void set_print_string(void (*i_print) (const char *buf));

private:

       int trcg(double delta, double *g, double *s, double *r); // 共轭梯度法，被tron调用

       double norm_inf(int n, double *x);

       double eps; // 收敛精度

       int max_iter; // 最大迭代次数

       function *fun_obj; // 目标函数

       void info(const char *fmt,...);

       void (*tron_print_string)(const char *buf);

};

4、重要算法的实际应用均有讲解

核心算法的实际应用都有介绍，对深度学习技术在计算机视觉、语音识别、自然语言处理、计算机图形学等领域的应用情况有详细而深入的介绍。这些内容能帮助读者掌握算法的实际应用方法、建模的思路。

❆

购买指南

目前本书在京东上七五折包邮预售：

 （扫码进入购买链接）

 

❆

目录

全书由21章组成，共分为三大部分。第1～3章为第一部分，介绍机器学习的基本原理、所需的数学知识（包括微积分、线性代数、概率论和优化方法），以及机器学习中的核心概念。第4～20章为第二部分，是本书的主体，介绍各种常用的有监督学习算法、无监督学习算法、半监督学习算法和强化学习算法。对于每种算法，从原理与推导、工程实现和实际应用3个方面进行介绍，对于大多数算法，都配有实验程序。第21章为第三部分，介绍机器学习和深度学习算法实际应用时面临的问题，并给出典型的解决方案。此外，附录A给出各种机器学习算法的总结，附录B给出梯度下降法的演化关系，附录C给出EM算法的推导。

注：在极市平台公众号后台回复《机器学习与应用》即可查看完整目录列表。

-阅读原文回帖参与免费赠书-