如何通俗地解释欧拉公式(e^πi+1=0)?
加入极市专业CV交流群,与10000+来自腾讯,华为,百度,北大,清华,中科院等名企名校视觉开发者互动交流!
同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流。关注 极市平台 公众号 ,回复 加群,立刻申请入群~
来源:算法与数学之美@微信公众号
1 复数
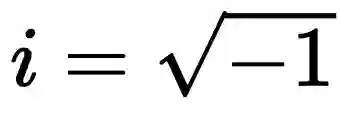 ,这个就是i的定义。虚数的出现,把实数数系进一步扩张,扩张到了复平面。实数轴已经被自然数、整数、有理数、无理数塞满了,虚数只好向二维要空间了。
,这个就是i的定义。虚数的出现,把实数数系进一步扩张,扩张到了复平面。实数轴已经被自然数、整数、有理数、无理数塞满了,虚数只好向二维要空间了。
从自然数扩张到整数:增加的负数可以对应“欠债、减少”
从整数扩张到有理数:增加的分数可以对应“分割、部分”
从有理数扩张到实数:增加的无理数可以对应“单位正方形的对角线的长度
从实数扩张到复数:增加的虚数对应什么?
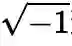 到底等于多少,我们规定
到底等于多少,我们规定
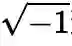 没有意义就可以了嘛,就好像1/0一样。
没有意义就可以了嘛,就好像1/0一样。
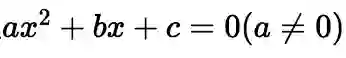 的万能公式:
的万能公式:
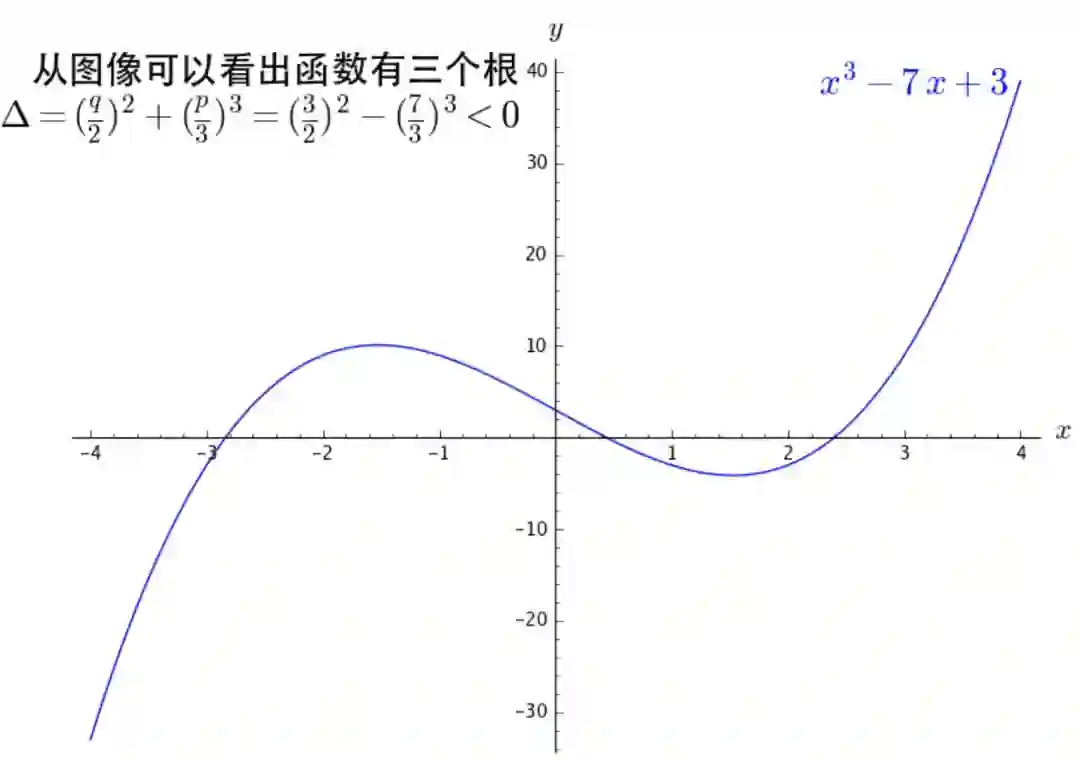
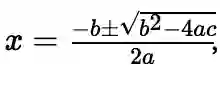 其判别式
其判别式
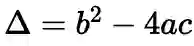


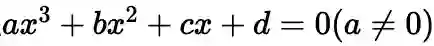 ,一元三次方程的解太复杂了,这里写不下,大家可以参考维基百科 ,但愿大家能够打开。
,一元三次方程的解太复杂了,这里写不下,大家可以参考维基百科 ,但愿大家能够打开。
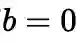 ,此时,一元三次方程可以化为
,此时,一元三次方程可以化为
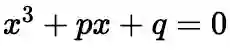 ,其根可以表示为:
,其根可以表示为:
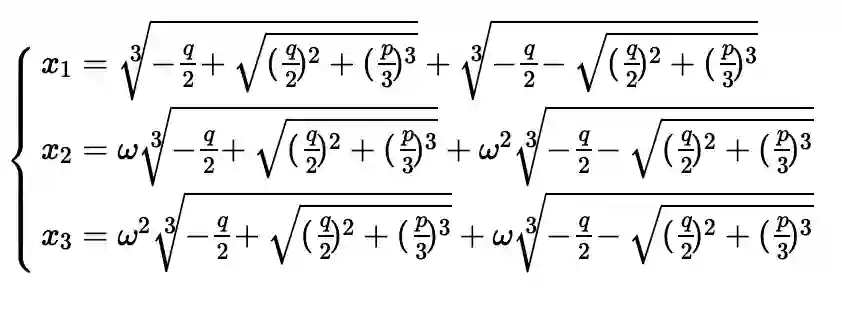
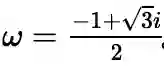
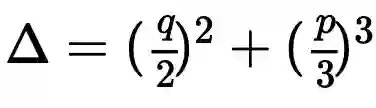 ,注意观察解的形式,
,注意观察解的形式,
 是被包含在根式里面的。
是被包含在根式里面的。

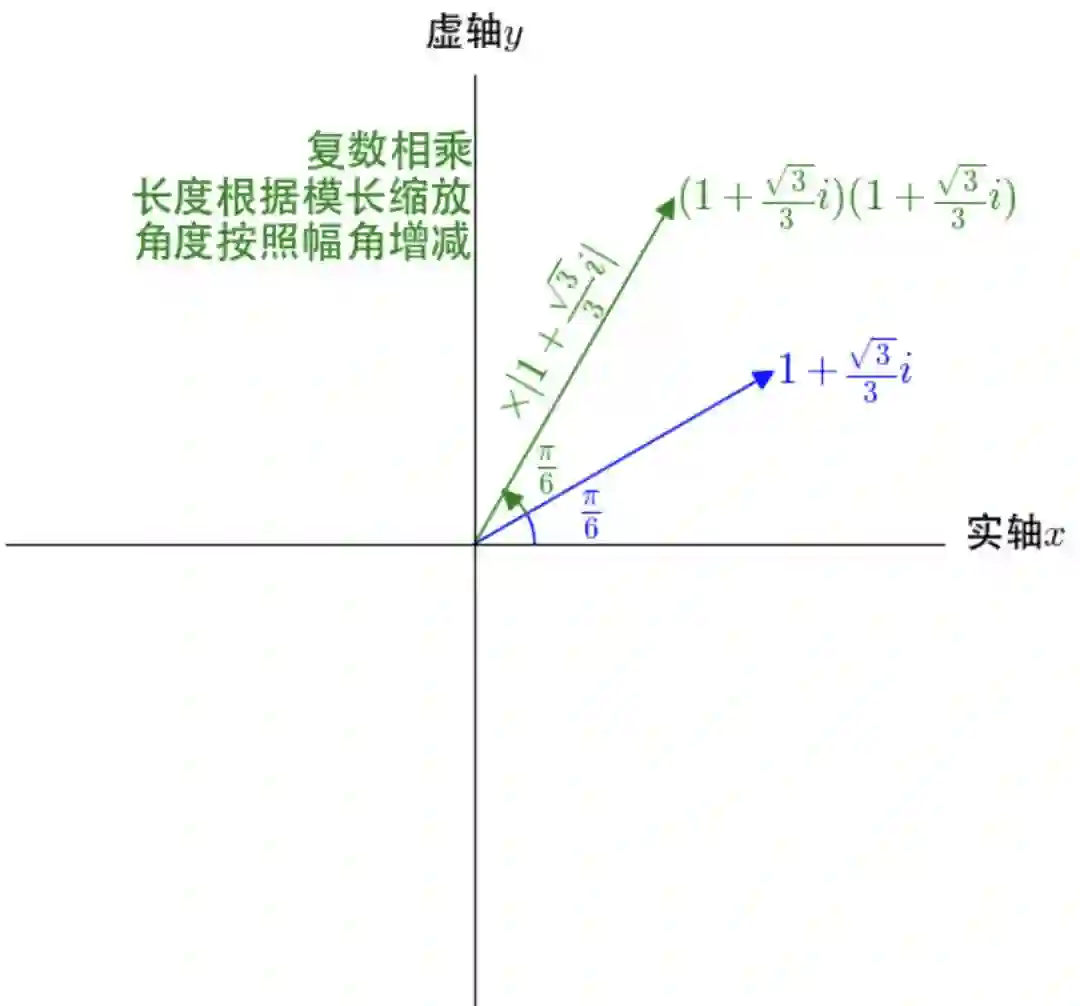
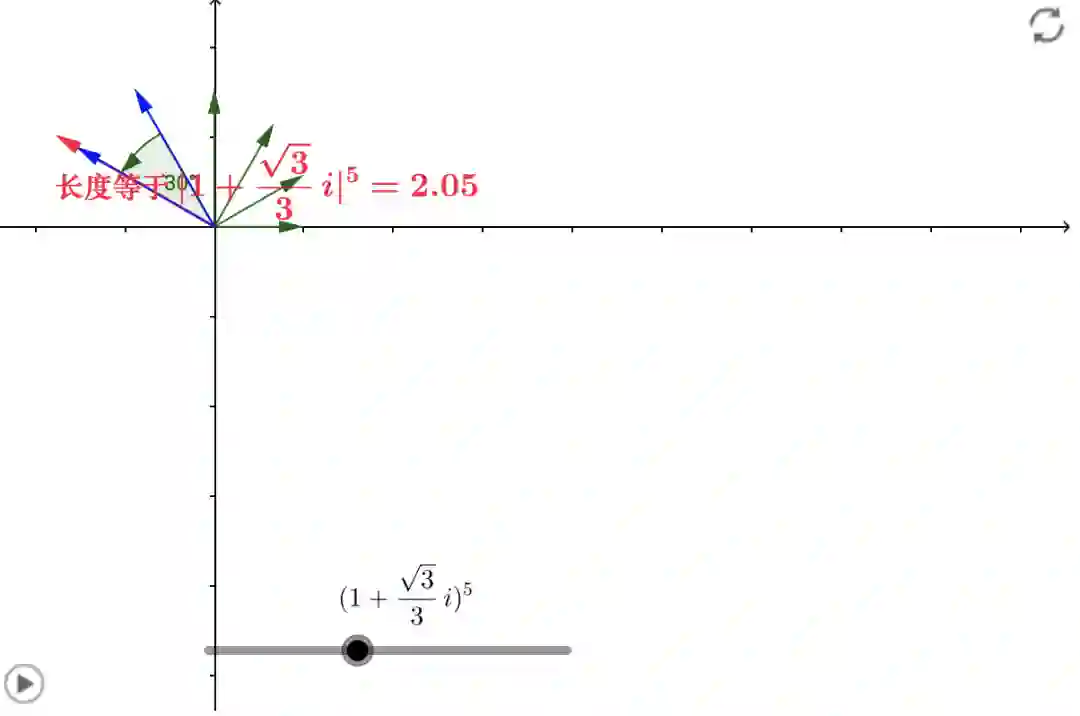
2 欧拉公式
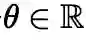 ,有
,有
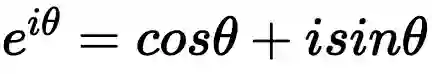
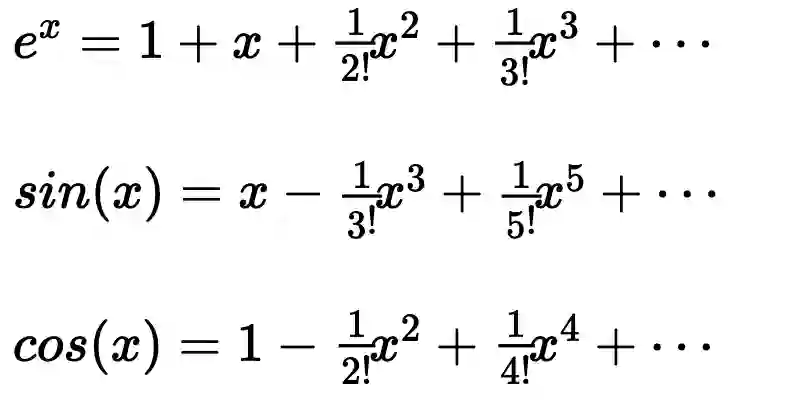
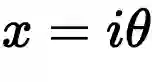 代入e可得
代入e可得
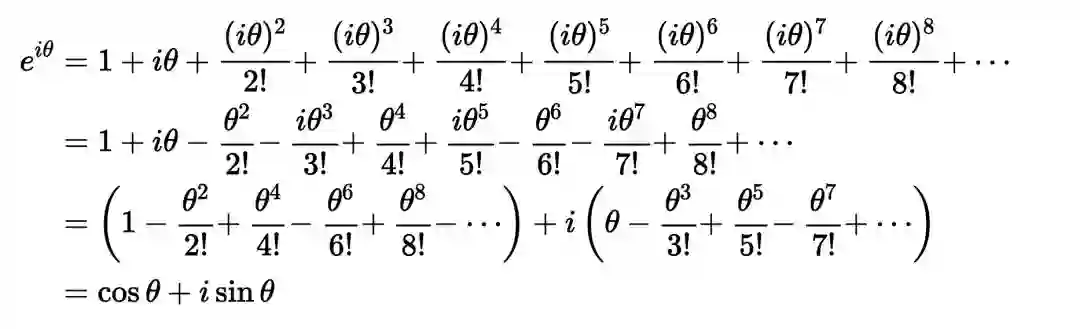
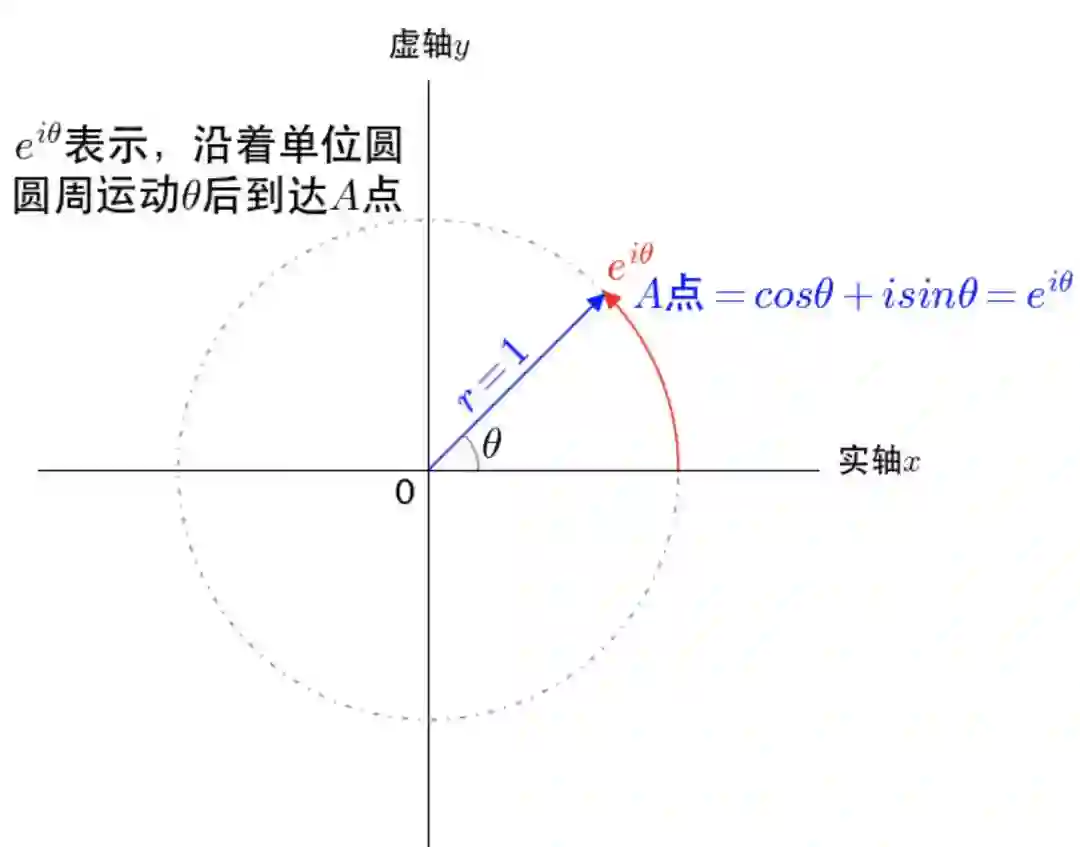
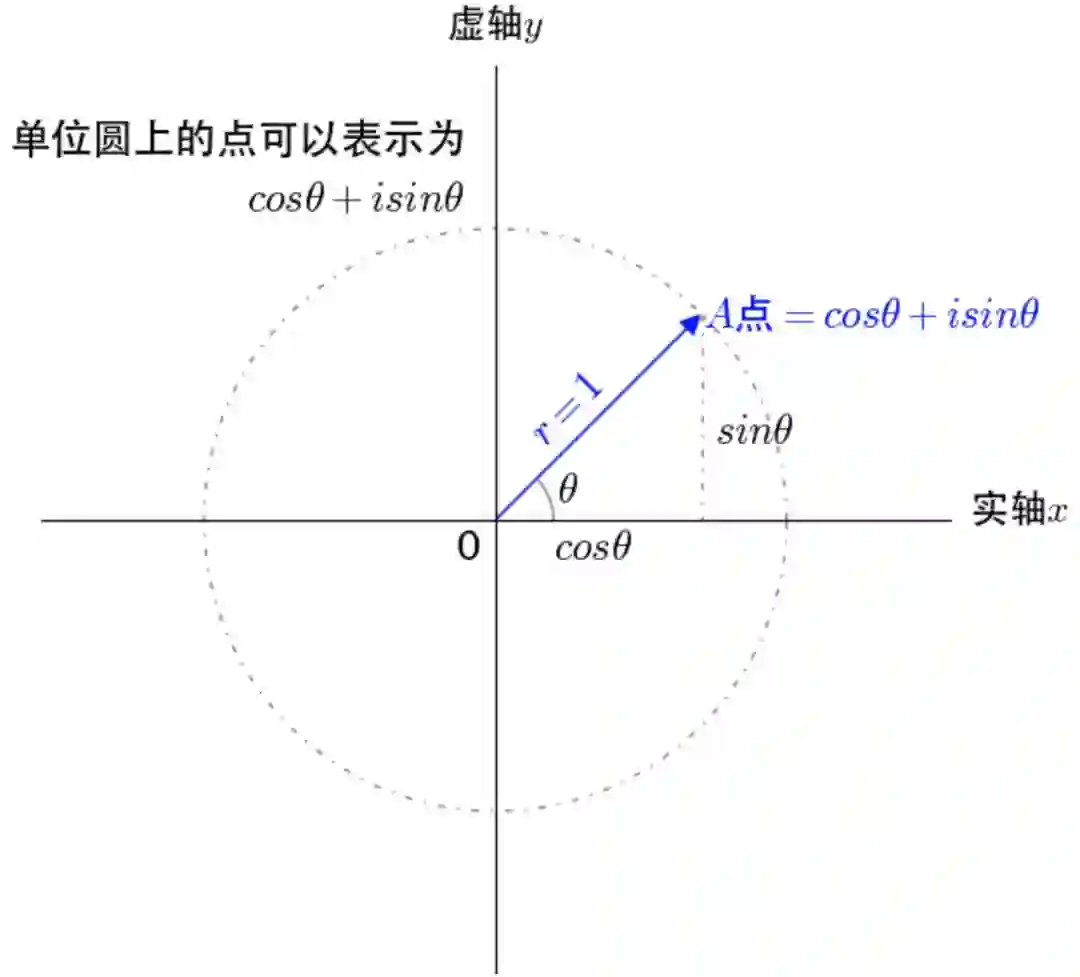
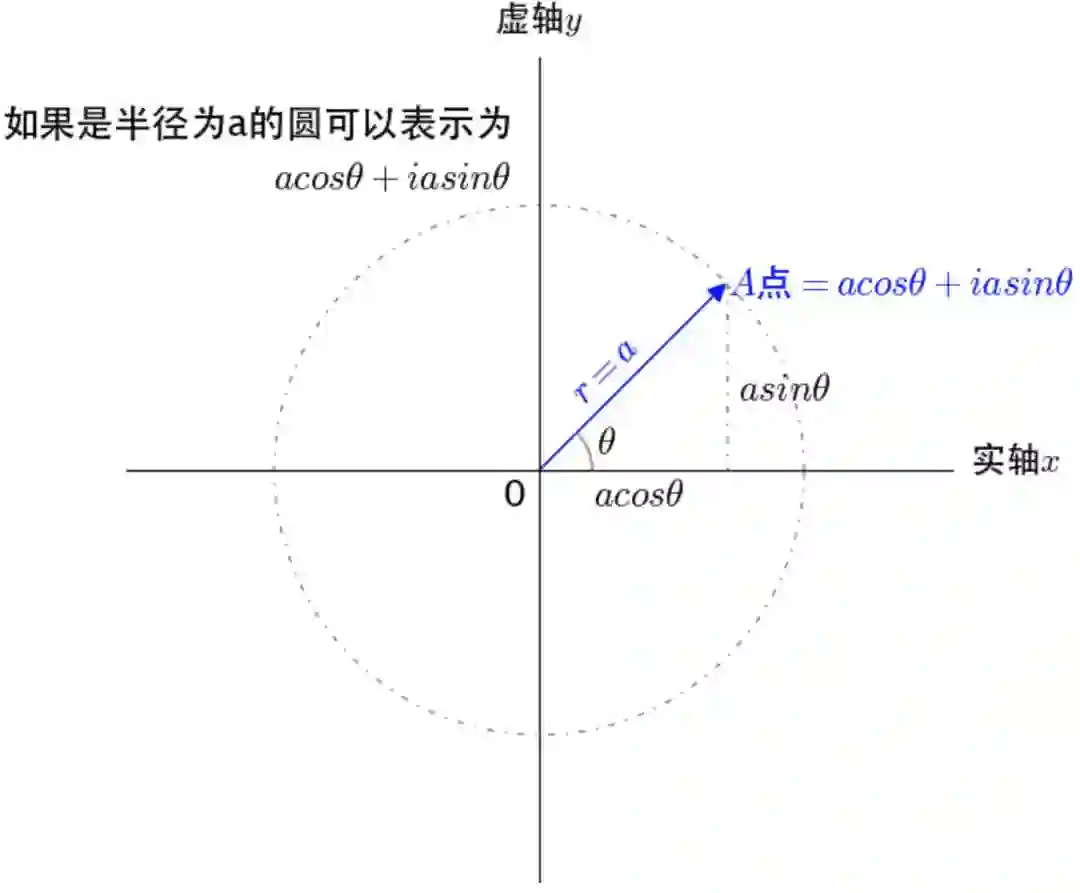
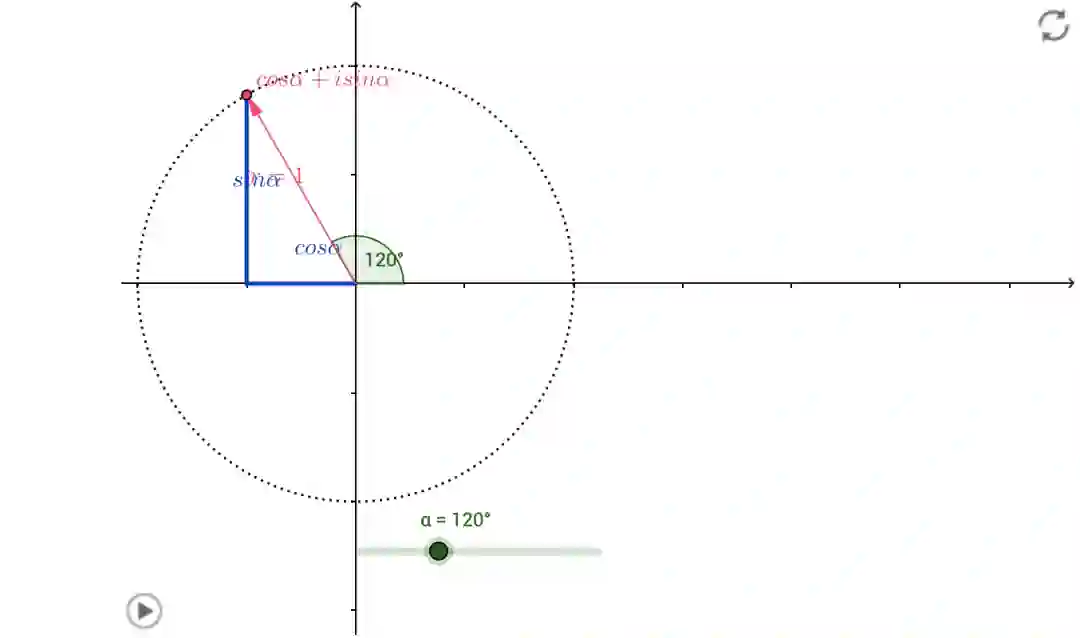
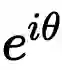 看作通过单位圆的圆周运动来描述单位圆上的点,
看作通过单位圆的圆周运动来描述单位圆上的点,
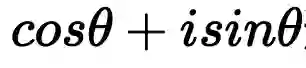 通过复平面的坐标来描述单位圆上的点,是同一个点不同的描述方式,所以有
通过复平面的坐标来描述单位圆上的点,是同一个点不同的描述方式,所以有
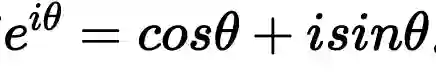
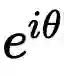 是圆周运动?
是圆周运动?
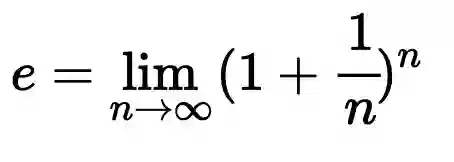
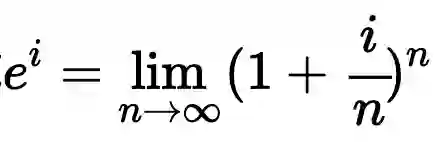 。根据之前对复数乘法的描述,乘上
。根据之前对复数乘法的描述,乘上
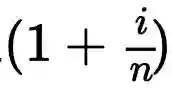 是进行伸缩和旋转运动,n取值不同,伸缩和旋转的幅度不同。
是进行伸缩和旋转运动,n取值不同,伸缩和旋转的幅度不同。
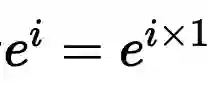 如何在圆周上完成1弧度的圆周运动的:
如何在圆周上完成1弧度的圆周运动的:
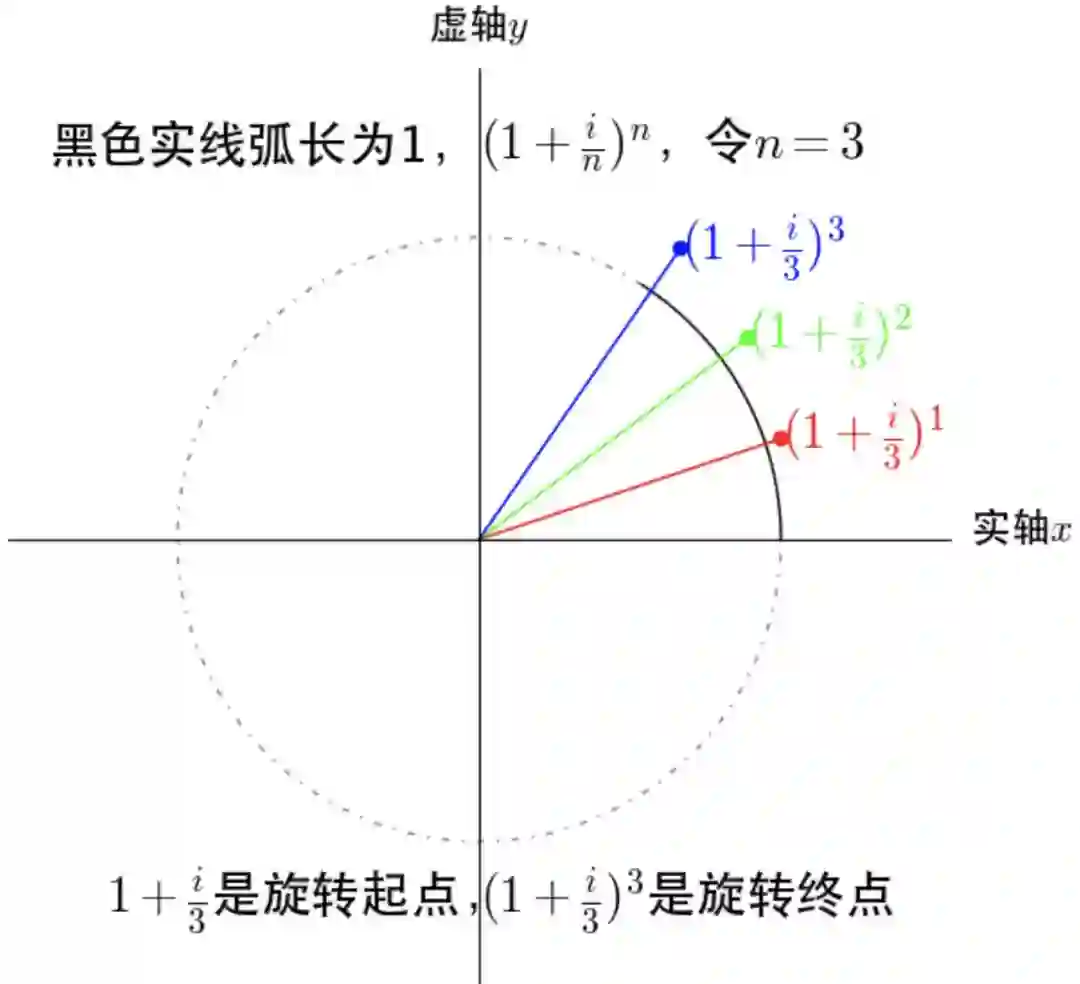
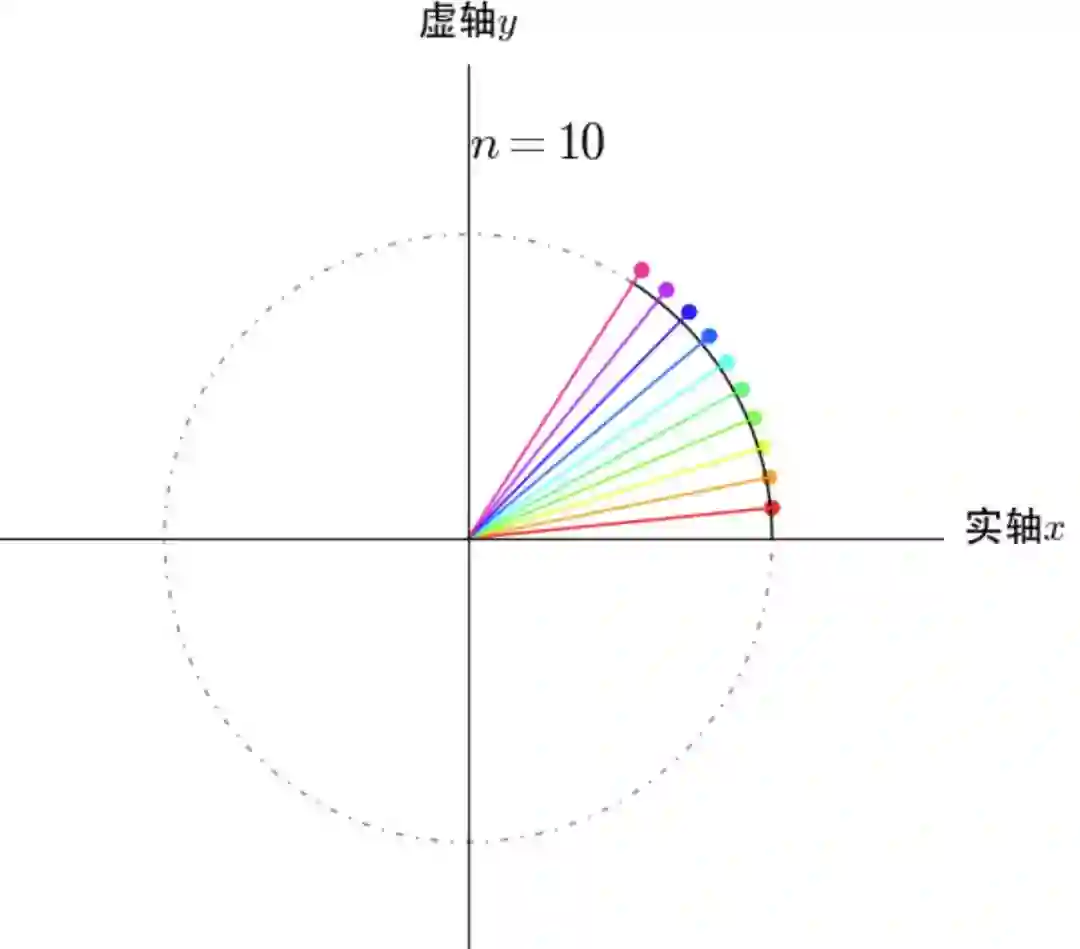
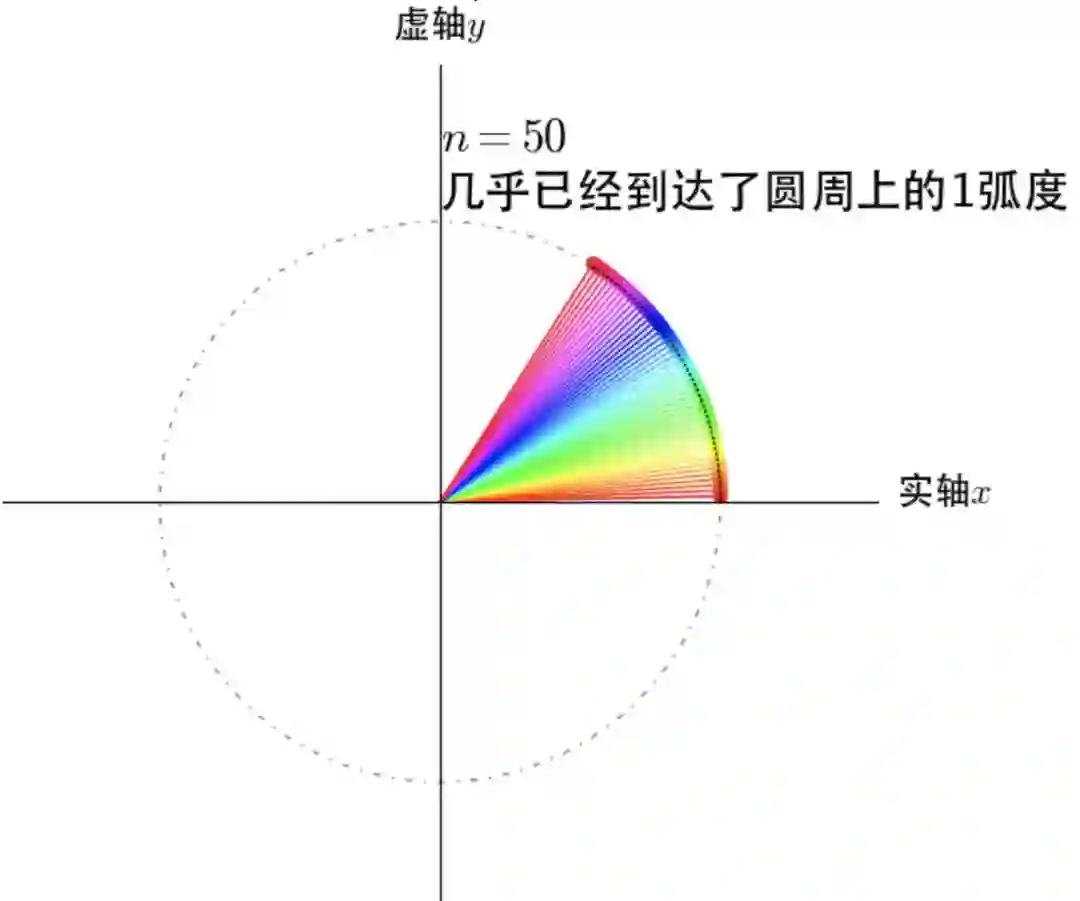
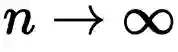 时,
时,
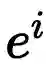 在单位圆上转动了1弧度。
在单位圆上转动了1弧度。
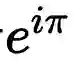 ,这个应该是在单位圆上转动
,这个应该是在单位圆上转动
 弧度:
弧度:
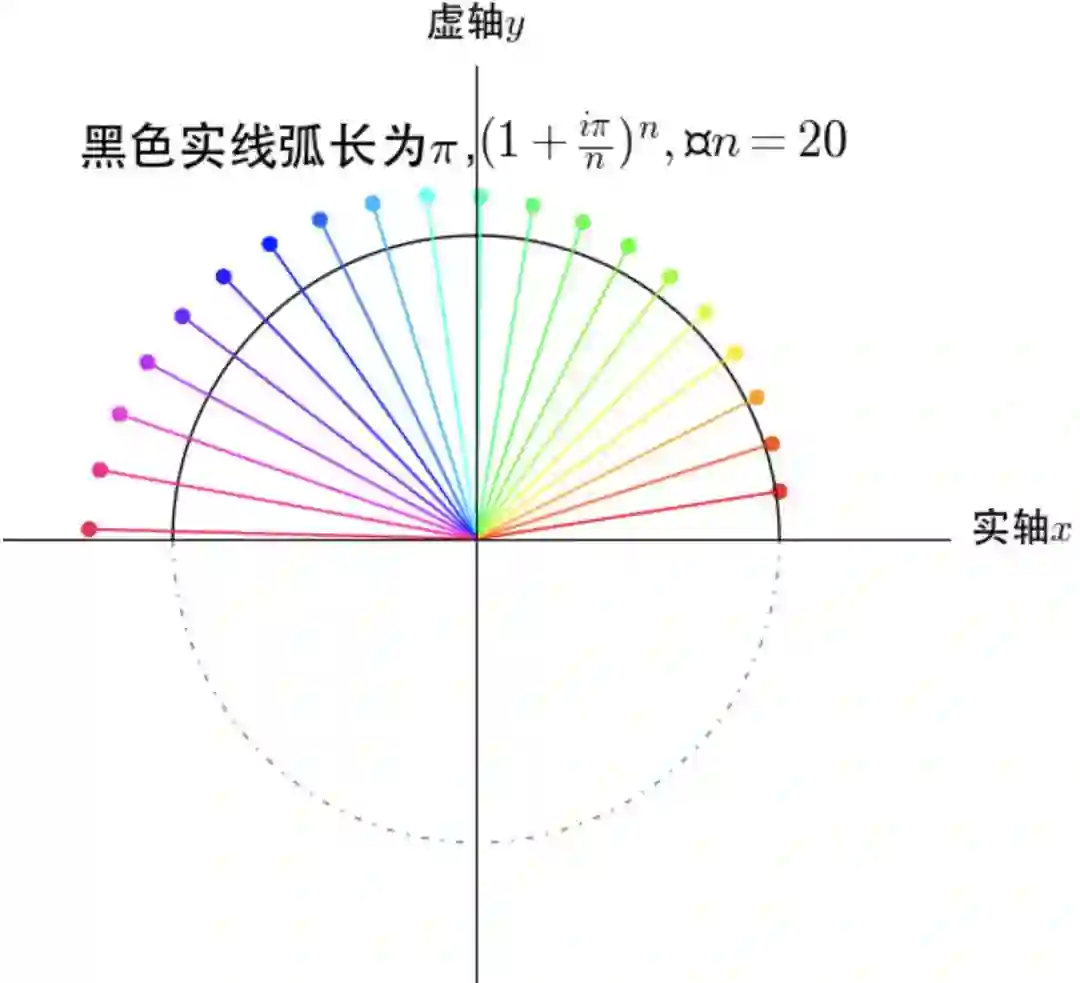
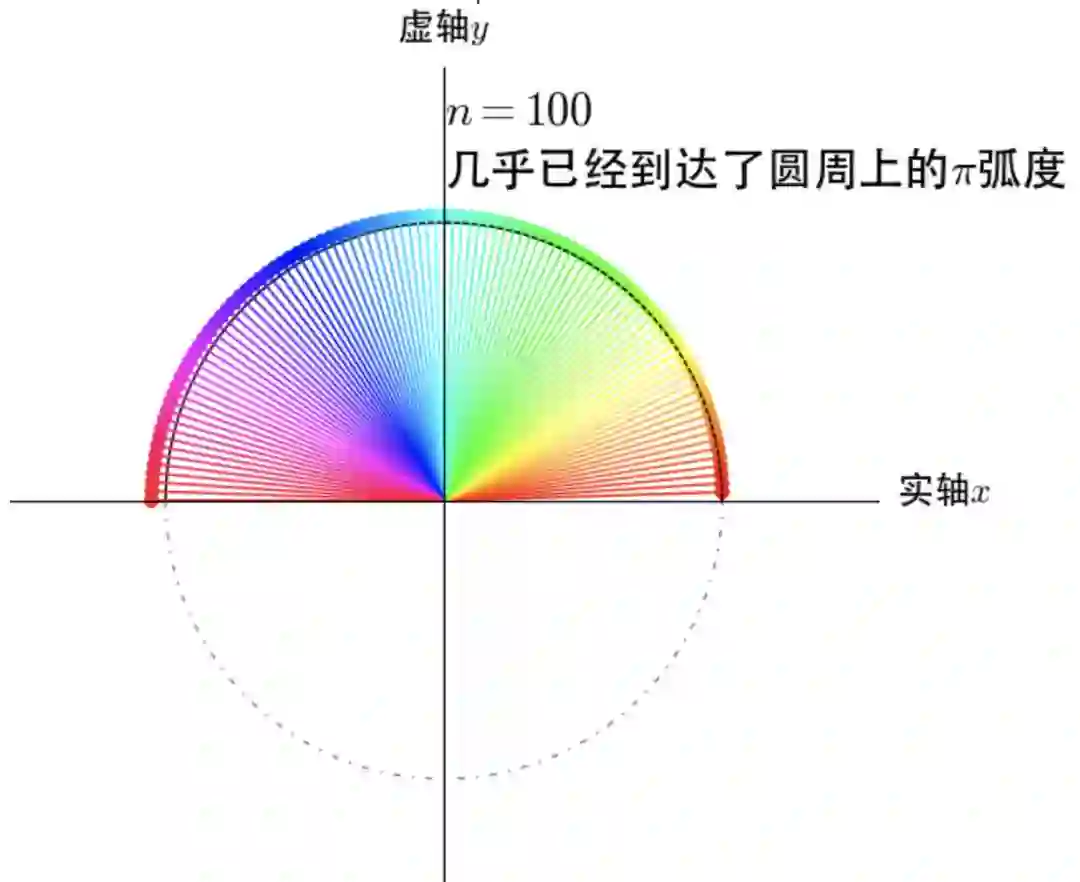
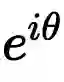 确实是单位圆周上的圆周运动。
确实是单位圆周上的圆周运动。
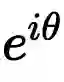 是如何运动的吧:
是如何运动的吧:
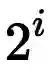 看不出来有什么几何含义,不过我们稍微做个变换
看不出来有什么几何含义,不过我们稍微做个变换
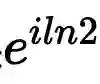 ,几何含义还是挺明显的,沿圆周运动
,几何含义还是挺明显的,沿圆周运动
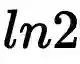 弧度。
弧度。
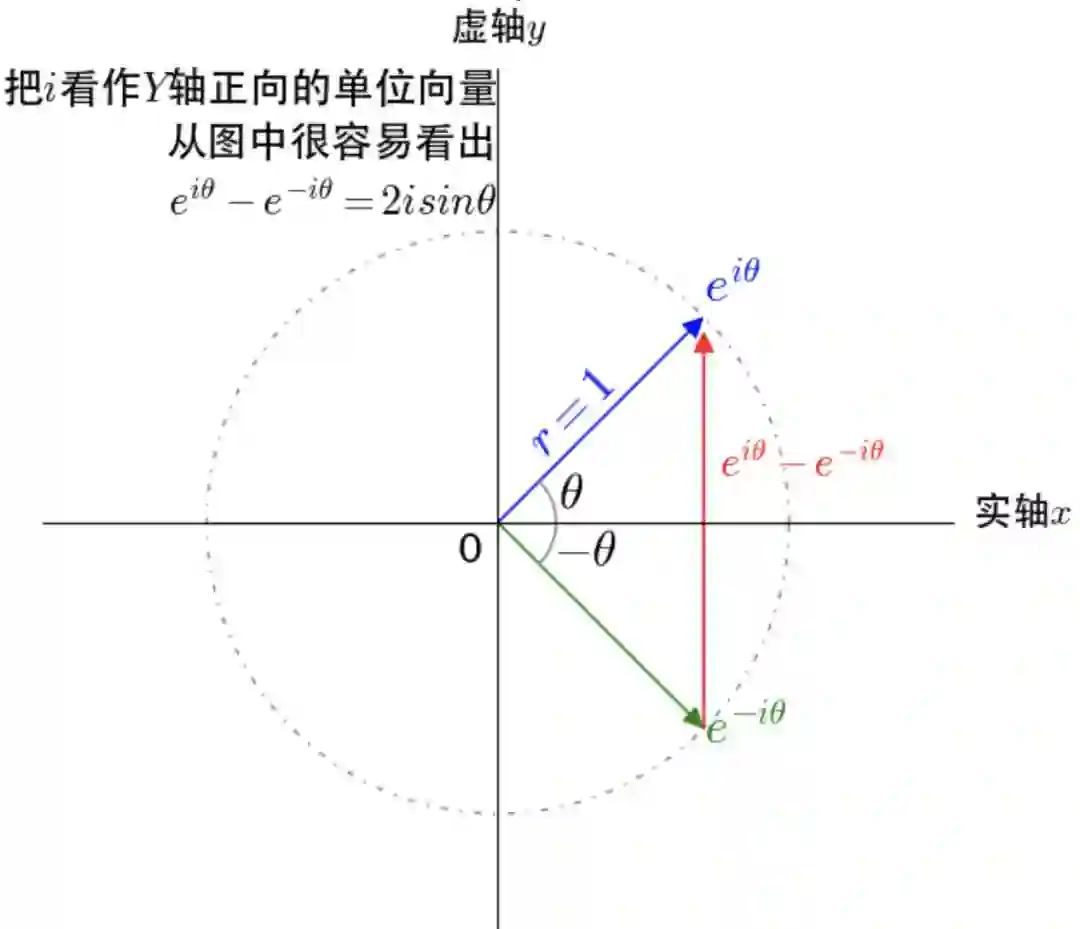
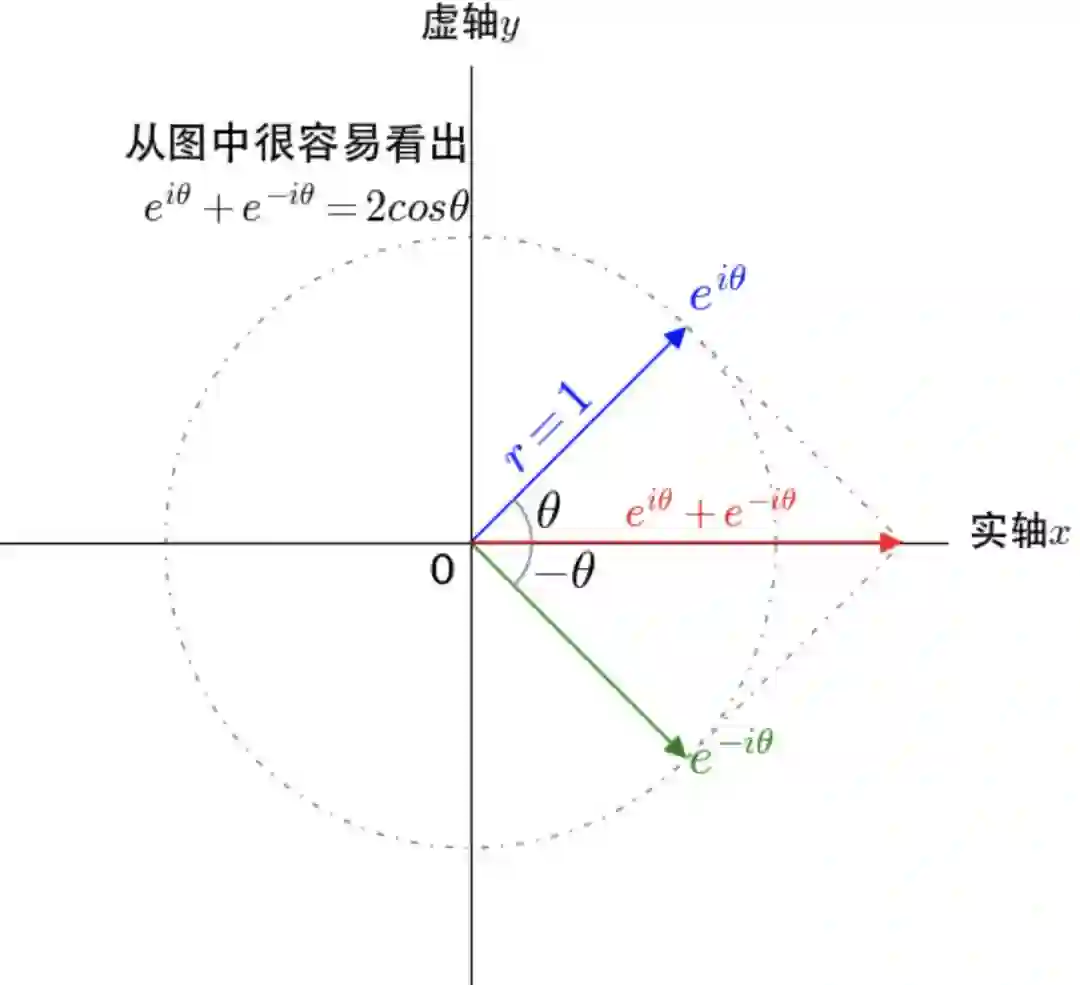
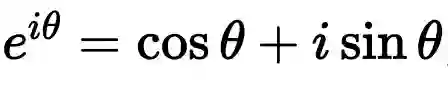 ,可以轻易推出:
,可以轻易推出:
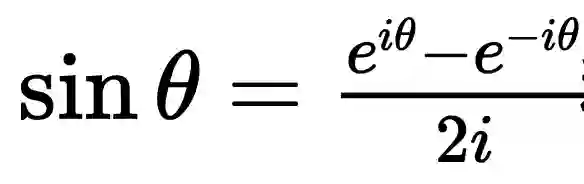 和
和
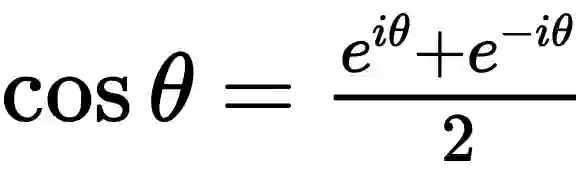
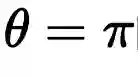 的时候,代入欧拉公式:
的时候,代入欧拉公式:
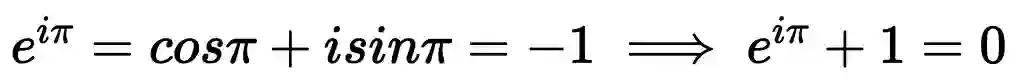
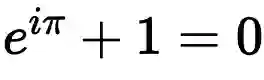 就是欧拉恒等式,被誉为上帝公式,
就是欧拉恒等式,被誉为上帝公式,
 乘法单位元1、加法单位元0,这五个重要的数学元素全部被包含在内,在数学爱好者眼里,仿佛一行诗道尽了数学的美好。
乘法单位元1、加法单位元0,这五个重要的数学元素全部被包含在内,在数学爱好者眼里,仿佛一行诗道尽了数学的美好。
*延伸阅读
△长按添加极市小助手
△长按关注极市平台,获取最新CV干货
觉得有用麻烦给个在看啦~
登录查看更多
相关内容
Arxiv
5+阅读 · 2018年11月1日
Arxiv
17+阅读 · 2018年3月20日
Arxiv
9+阅读 · 2018年1月27日








