WWW 2022 ：基于纯MLP架构的序列推荐模型

会员服务 ·

WWW 2022 ：基于纯MLP架构的序列推荐模型

2022 年 3 月 20 日 专知

机构｜中国科学院大学地质与地球物理研究所

研究方向｜人工智能与固体地球物理学

机构｜中国人民大学信息学院

研究方向｜序列表示学习

本文主要提出了一个基于纯MLP架构的序列化推荐模型，其通过可学习滤波器对用户序列进行编码，在8个序列化推荐数据集上超越了Transformer等模型。

论文题目：Filter-enhanced MLP is All You Need for Sequential Recommendation

论文下载地址：https://www.zhuanzhi.ai/paper/349d7bc0d4de186d2ad9691f0236a272

论文开源代码：https://github.com/RUCAIBox/FMLP-Rec

Filter-enhanced MLP is All You Need for

Sequential Recommendation

Kun Zhou*,Hui Yu*,Wayne Xin Zhao and Ji-Rong Wen

前言

越来越多的工作表明复杂的Transformer架构可能不是进行序列表示建模的最优模型，其中过多的参数量反而一定程度上带来了过拟合的风险，该风险在某些噪声较大的场景下会严重影响模型效果（如：推荐系统和信号处理）。本文针对序列化推荐问题，通过一系列分析实验发现该场景下滤波算法可以减少该过拟合问题并极大提升Transformer模型的效果，且在Transformer架构基础上将multi-head attention替换为频域下的MLP层，可以模拟滤波机制并进一步提升模型效果。最终我们提出了FMLP-Rec (Filter-enhanced MLP approach for sequential recommendation)，一个纯MLP架构的模型以进行用户历史序列的编码并完成推荐任务。由于我们是在频域下利用MLP进行序列编码，我们的时间复杂度低于Transformer结构但是却有着相同的感受野。在8个数据集上的大量实验证明了我们的纯MLP模型可以超越基于RNN，CNN，GNN和Transformer的模型。

一. 研究背景与动机

1. 序列化推荐

在现实世界中，用户的前后行为都存在强烈的关联性与因果性，将用户过去的这一系列交互行为视作用户行为序列 $u=\{i_1,i_2……i_n\}$ ，并通过构建模型对其建模，来预测下一时刻用户最感兴趣的内容 $i_{n+1}$ ，这就是序列化推荐（Sequential Recommendation）的核心思想。目前序列化推荐的常用模型包括RNN、CNN、GNN以及Transformer。

2. 滤波算法

用户的历史行为数据会不可避免地包含噪音，将其输入复杂的神经网络模型（如Transformer）后，很容易导致过拟合问题。为了解决这个问题，我们借助在数字信号处理领域被广泛应用的滤波器（Filter）来进行处理。滤波器是一种选频装置，可以使特定频率成分的信号通过/阻断，常常用于过滤现实场景下的噪声信号。在信号进入滤波器之前，需要从时间域转换到频率域，傅里叶变换（Fourier Transform）就是这样的一个工具。如：低通滤波器（LPF: Low-Pass Filter）：使低频成分通过、并极大地衰减其他频率成分的一种滤波器；带阻滤波器（BSF: Band-Stop Filter）：通过设定上下边界，使该频率区间内的成分阻断，但不影响区间外频率信息的滤波器；由于用户行为序列中有用信号和噪音的频率成分存在差异，傅里叶变换后，在频率域中就变得易于区分，再通过设计特定频率响应的滤波器阻断噪音所在频带，能显著地降低噪音影响。

二. 先导实验

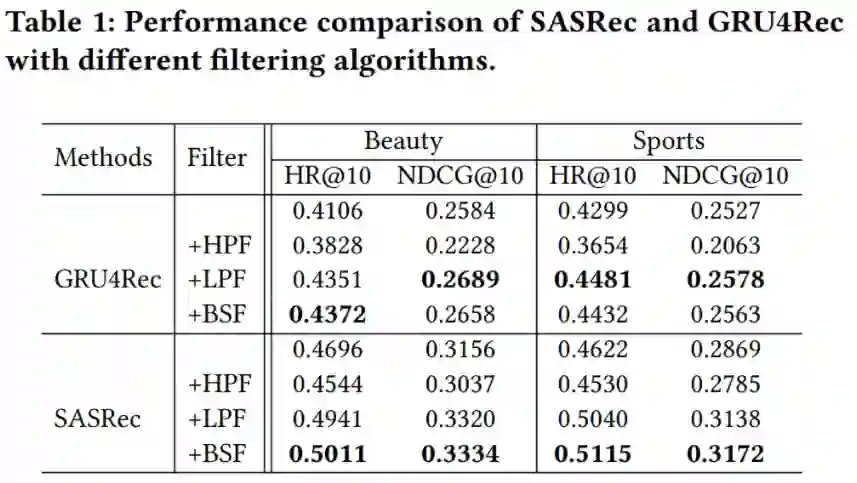
1.基于Transformer与RNN的序列推荐模型中加入滤波器

我们首先制作了简易的高通（HPF）、低通（LPF）、带阻（BSF）三种不同类型的滤波器，放置于GRU4Rec（基于RNN）和SASRec（基于Transformer）模型的Embedding层与Encoder层之间，不对其它部分做任何改动，在不同数据集上进行训练，表现大致相同并且结果令我们惊喜，表1中列出了在Beauty和Sports数据集上的结果，可以清楚地看到低通滤波器、带阻滤波器给GRU4Rec、SASRec的性能带来了持续且显著的提升。

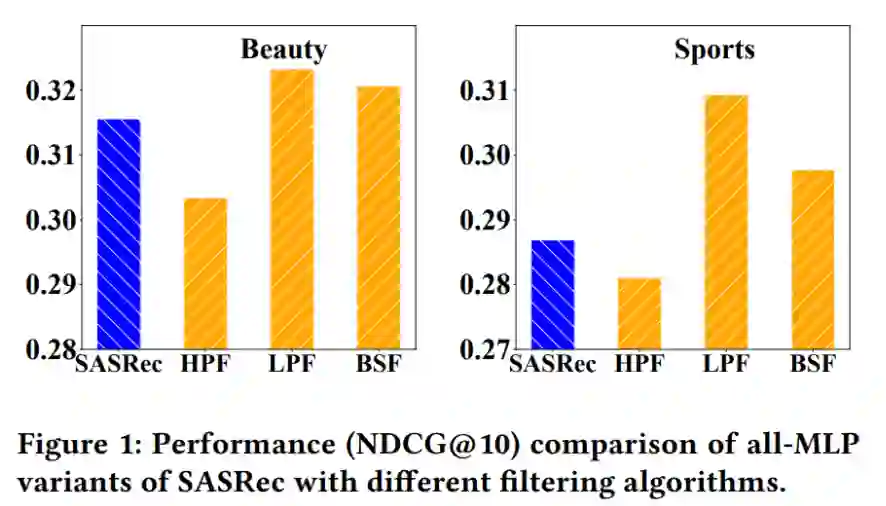
2.移除Transformer中多头注意力，仅保留MLP和滤波器

我们更进一步将SASRec中的多头自注意力机制（mutil-head self-attention）换为之前用到的三种滤波器，这样得到的模型就是一个全MLP模型。我们将这种模型与SASRec在相同的数据集上进行测试，结果对比见图1。不难看出，结构简易的、添加了低通滤波器的MLP模型，在性能上大幅超越了设计复杂的、基于自注意力机制SASRec模型，这表明合适的滤波器与全MLP模型的组合是十分适用于序列化推荐领域的，这种组合能够在保持模型轻量化的同时，降低信号噪音，有效减弱过拟合现象。

三. FMLP-Rec模型

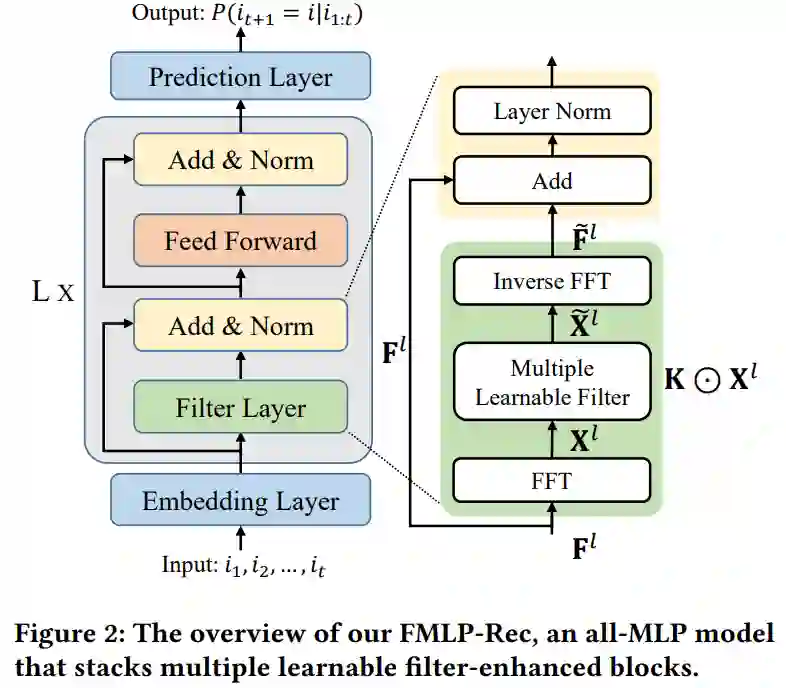
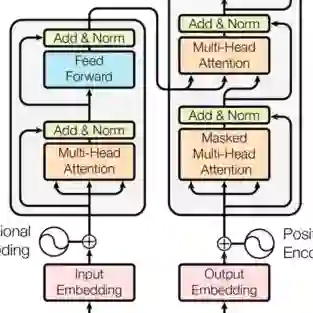
基于上述两个实验，我们考虑将以上的简单滤波算法替换成可学习的滤波器层（Learnable Filters），依赖梯度下降算法进行优化，使其能够自适应地变换滤波器的频率响应，对序列进行处理，达到降噪的效果。我们提出了FMLP-Rec，这是一个全MLP的模型。FMLP-Rec的模型结构如下图所示，其基础网络架构与SASRec相似，最大的区别就是将SASRec中Transformer的多头自注意力机制替换为一个滤波器层，利用这种机制提取序列特征。该滤波器层是通过在频域下的矩阵点乘来实现的，其等价于时域中的循环卷积，在时间复杂度更低的情况下并能够提供更大的感受野。

1. Embedding Layer

FMLP-Rec与SASRec一致，通过对输入序列进行item-embedding和position-embedding，将item映射到高维空间中，并为用户行为序列引入先后位置关系，传入模型的编码层。

2. Learnable-Filter-enhanced Blocks

Filter Layer

FMLP-Rec的编码层是通过可学习的滤波增强模块（Learnable Filter-enhanced Block）的堆叠来实现的，该模块的核心是一个滤波器层。用户行为序列经Embedding层后输入滤波器层，此时会经过一次快速傅里叶变换（FFT）转换到频率域：

$X^l = \mathcal{F}(F^l)$

其中 $F^l \in \mathbb{R}^{n \times d}$ ， $n$ 是序列长度， $d$ 是Embedding的维度， $l$ 表示序列经过 $l$ 个可学习的滤波增强模块，若是从Embedding层直接输入的，那么 $l=0$ ， $\mathcal{F}$ 表示快速傅里叶变换，变换后的 $X^l$ 为复数且 $X^l \in \mathbb{C}^{n \times d}$ 。

经过傅里叶变换后的序列 $X^l$ 在频率域中与一个相同尺寸的可学习滤波器 $K$ 进行点乘，使其频谱成分发生改变，并且滤波器通过随机梯度下降在每一轮训练中进行更新，达到自适应滤波的效果：

$\widetilde X^l = K ⊙ X^l$

频率域滤波后的序列用 $\widetilde X^l$ 表示，此时噪音的频率成分已经得到压制，对其傅里叶逆变换得到：

$\widetilde F^l = \mathcal{F^{-1}}(\widetilde X^l)$

$\mathcal{F^{-1}}$ 表示快速傅里叶逆变换， $\widetilde F^l$ 表示经过滤波后时间域中的用户行为序列。

从理论上来说，这种频率域的可学习滤波器与序列的点乘，相当于在时间域对其进行循环卷积，即 $h * f^l = \mathcal{F^{-1}}(k ⊙ x^l)$ ，证明如下：

$\begin{align*} \mathcal{F}(h(t) * f^l(t)) &= \int_{-\infty}^\infty [\int_{-\infty}^\infty h(\tau)f(t-\tau) d\tau ]e^{-j\omega t} dt \\ &= \int_{-\infty}^\infty h(\tau)[\int_{-\infty}^\infty f(t-\tau) e^{-j\omega t} dt] d\tau \\ &= x^l(\omega)\int_{-\infty}^\infty h(\tau) e^{-j\omega\tau} d\tau \\ &= x^l(\omega) k(\omega) \end{align*}$

$\widetilde F^l$ 输入Dropout层后会进行一次残差连接，最后进入Layer Norm层。这三种机制的应用是为了防止训练中的梯度消失以及不稳定的问题，并且能降低过拟合现象，用公式表示为：

$\widetilde F^l = LayerNorm(F^l +Dropout(\widetilde F^l))$

Feed-forward Layers

模块后半部分是一个前馈层（双层MLP）与Add & Norm层的组合。通过前馈层引入非线性关系：

$FFN(\widetilde F^l) = (ReLU(\widetilde F^lW_1+b_1))W_2+b_2$

Add & Norm与Filter Layer模块中一致，通过Dropout、残差连接、Layer Normalization来防止过拟合，让模型有能力堆叠更多层来加深网络结构。

3. Prediction Layer

在经过若干滤波增强模块后，用户行为序列的特征得到有效提取，这时通过预测层对其处理，得到用户下一个最感兴趣的物品。

四. 实验结果

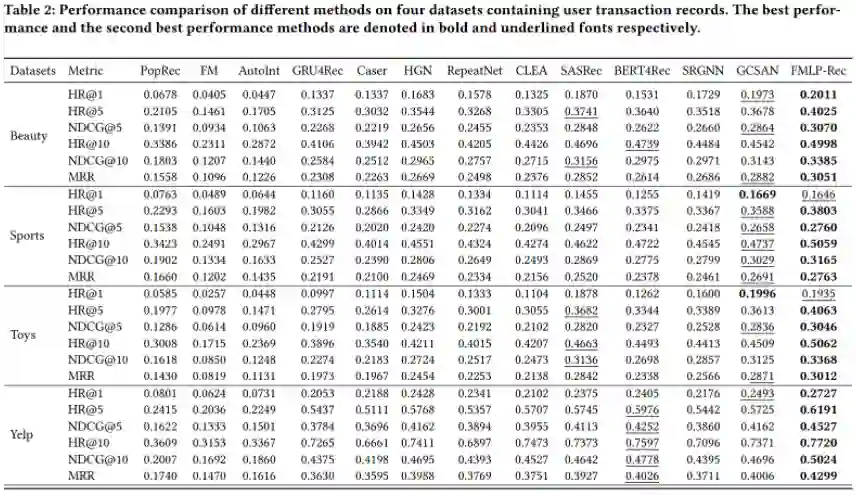
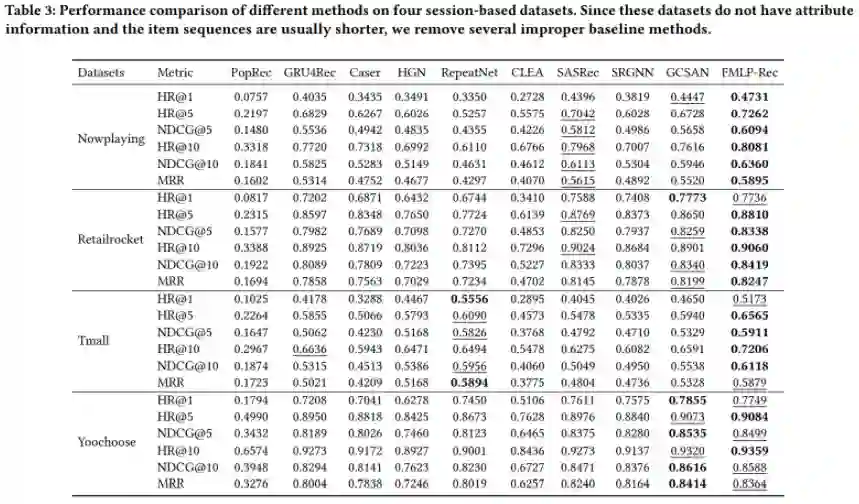
1. 在8个数据集上的主实验

我们在8个数据集上训练了不同神经网络架构的序列化推荐模型，其中4个数据集是按用户进行记录的，包含了用户以往的购买记录，分别是从亚马逊平台获取的Beauty，Sport，Toys数据集和Yelp数据集；其余4个数据集是按会话进行记录的，分别是Nowplaying，RetailRocket，Tmall以及Yoochoose数据集，训练结果整理在下表中。通过对比可以清晰地看出FMLP-Rec性能的优越性，它在所有数据集中的表现都大幅领先其他模型，而这些都是在网络结构和时间复杂度大幅降低的同时所实现的。

2. 滤波层的通用性

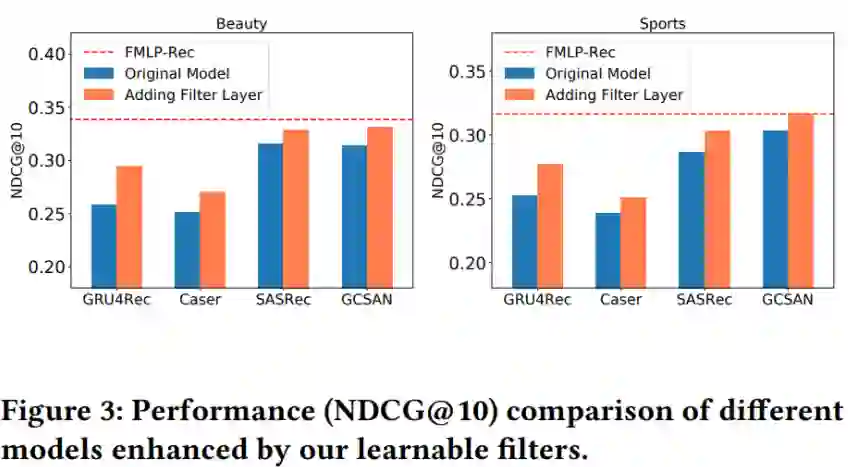
我们还设计了实验来证明在FMLP-Rec中起关键作用的滤波器层有望作为一个通用的网络模块，添加到其他模型中来处理序列化推荐任务，来提升这些模型的性能。于是，我们分别选取了基于RNN的GRU4Rec、基于CNN的Caser、基于GNN的GCSAN和基于Transformer的SASRec作为基准模型，然后将可学习的滤波器层添加到这些模型的Embedding层和Encoder层之间，在不同数据集中进行训练，与原始模型的结果对比见下图。可以看出，在加入可学习的滤波器层之后，所有模型的的表现都超过了原始模型，证明了滤波器层的加入能够明显减弱这些神经网络受噪音影响的现象，但是另一方面，这些加入了滤波器层之后的模型依旧没能比我们的FMLP-Rec表现更好，这表明可学习的滤波器层与参数更少的MLP结构的组合是更适用于序列化推荐任务的。

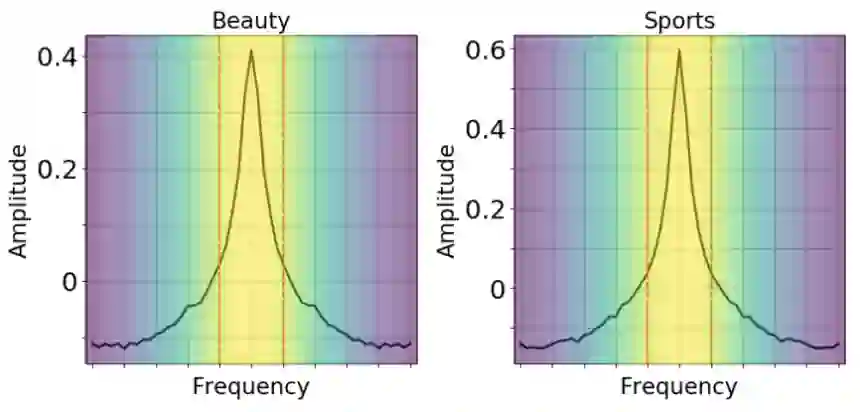
3. 滤波层的可视化

在实验的最后，我们从训练完成的模型中输出了FMLP-Rec的可学习滤波器，并且选取Beauty和Sports数据集上训练的滤波器制作成图，可以看到不同数据集上的滤波器形状大致相同。图中由黄色到紫色表示频率由低到高，那么这些滤波器的形状可以近似看做一种低通滤波器，红色虚线之内的低频成分基本为正向增益，其余部分随着频率升高，逐渐从衰减变为较弱的反向增益。

五. 总结

在序列化推荐任务中，用户的行为信息会不可避免地包含噪音，这会影响复杂的序列编码模型的效果。我们通过引入数字信号处理中的滤波器的思想，通过引入滤波机制，并舍弃Transformer中的复杂模块，最终得到一个基于可学习滤波器的纯MLP模型————FMLP-Rec。滤波器层本质上是一个频域下的MLP层，其可以在训练过程中通过随机梯度下降可以自适应地对用户行为序列中不同频段滤波机制进行调整，理论上来说等同于时间域的循环卷积，其更易于提取周期信号，并且同时兼具全局感受野和更低的时间复杂度。FMLP-Rec模型在8个数据集上击败了目前SOTA的基于RNN、CNN、GNN以及Transformer的神经网络模型。

专知便捷查看