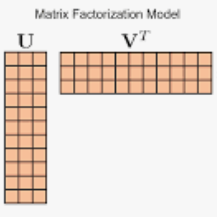
从原理到落地,七大维度详解矩阵分解推荐算法


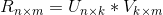
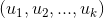 乘以标的物特征矩阵
乘以标的物特征矩阵
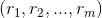 。
。
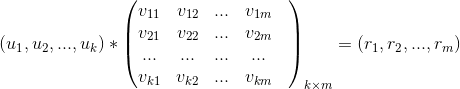
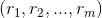 后,从该评分中过滤掉用户已经操作过的标的物,针对剩下的标的物得分做降序排列取 topN 推荐给用户。
后,从该评分中过滤掉用户已经操作过的标的物,针对剩下的标的物得分做降序排列取 topN 推荐给用户。
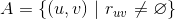 ,通过矩阵分解将用户
,通过矩阵分解将用户
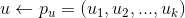
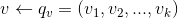
 ,真实值与预测值之间的误差为
,真实值与预测值之间的误差为
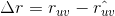 。如果预测得越准,那么
。如果预测得越准,那么
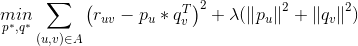
 是正则项,避免模型过拟合。通过求解该最优化问题,我们就可以获得用户和标的物的特征嵌入(用户的特征嵌入
是正则项,避免模型过拟合。通过求解该最优化问题,我们就可以获得用户和标的物的特征嵌入(用户的特征嵌入
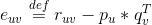
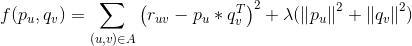
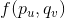 对
对
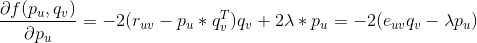
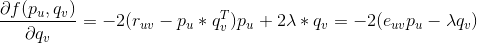
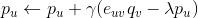
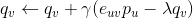
 来预测,但是不同的人对标的物的评价可能是不一样的,有的人倾向于给更高的评分,而有的人倾向于给更低的评分。对于同一个标的物,也会受到外界其他信息的干扰,影响人们对它的评价(比如视频,可能由于主演的热点事件导致该视频突然变火),这两种情况是由于用户和标的物引起的偏差。我们可以在这里引入 Bias 项,将评分表中观察到的值分解为 4 个部分:全局均值( global average ),标的物偏差( item bias ),用户偏差( user bias )和用户标的物交叉项( user-item interaction )。这时,我们可以用如下公式来预测用户 u 对标的物 v 的评分:
来预测,但是不同的人对标的物的评价可能是不一样的,有的人倾向于给更高的评分,而有的人倾向于给更低的评分。对于同一个标的物,也会受到外界其他信息的干扰,影响人们对它的评价(比如视频,可能由于主演的热点事件导致该视频突然变火),这两种情况是由于用户和标的物引起的偏差。我们可以在这里引入 Bias 项,将评分表中观察到的值分解为 4 个部分:全局均值( global average ),标的物偏差( item bias ),用户偏差( user bias )和用户标的物交叉项( user-item interaction )。这时,我们可以用如下公式来预测用户 u 对标的物 v 的评分:
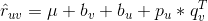
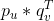 是用户与标的物交叉项。那么最终的优化问题就转化为:
是用户与标的物交叉项。那么最终的优化问题就转化为:
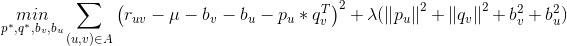
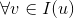 ,
,
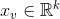 是用户对标的物v的隐式反馈的嵌入特征向量(这里为了简单起见,我们不区分用户的各种隐式反馈,只要用户做了一次隐式反馈,认为有隐式反馈,即是采用布尔代数的方式来处理隐式反馈)。那么对用户所有的隐式反馈
是用户对标的物v的隐式反馈的嵌入特征向量(这里为了简单起见,我们不区分用户的各种隐式反馈,只要用户做了一次隐式反馈,认为有隐式反馈,即是采用布尔代数的方式来处理隐式反馈)。那么对用户所有的隐式反馈
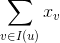
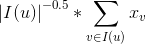
 ,
,
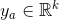 是属性
是属性
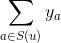
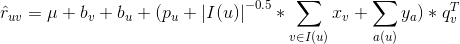
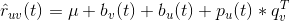
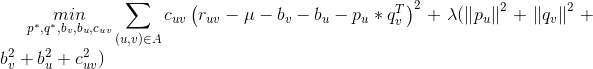

 ,效果比较好。
,效果比较好。
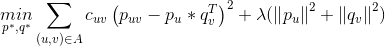
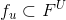 是用户 u 的特征表示(每个用户用一系列特征来表示)。同理,
是用户 u 的特征表示(每个用户用一系列特征来表示)。同理,
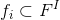 表示标的物i的特征集合。
表示标的物i的特征集合。
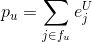
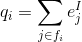
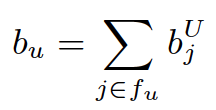 ,
,
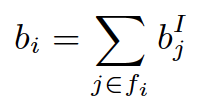 表示用户 u 和标的物 i 的 bias 向量表示。那么,用户 u 对标的物i的预测评分可以用如下公式表示
表示用户 u 和标的物 i 的 bias 向量表示。那么,用户 u 对标的物i的预测评分可以用如下公式表示
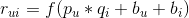
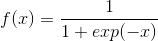
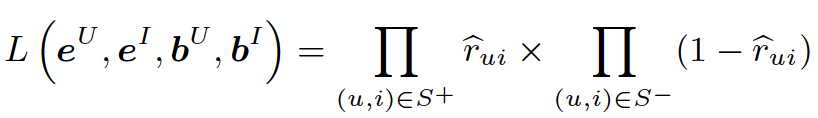
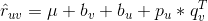
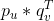 是用户标的物交叉项。那么最终的优化问题就转化为:
是用户标的物交叉项。那么最终的优化问题就转化为:
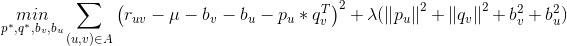
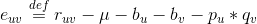
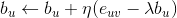
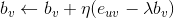
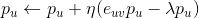
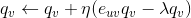
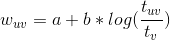
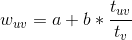
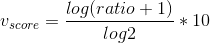
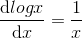 是自变量 x 的递减函数,即导数(斜率)是单调递减函数,当自变量 x 越大时,函数值增长越慢,因此基于该公式的数学解释可以说明对数函数是满足经济学上的“边际效应递减”这一原则的。针对视频来说,意思就是你在看前面十分钟代表的兴趣程度是大于在最后看十分钟的,这就像你在很饿的时候,吃前面一个馒头的满足感是远大于吃了 4 个馒头之后再吃一个馒头的满足感的。
是自变量 x 的递减函数,即导数(斜率)是单调递减函数,当自变量 x 越大时,函数值增长越慢,因此基于该公式的数学解释可以说明对数函数是满足经济学上的“边际效应递减”这一原则的。针对视频来说,意思就是你在看前面十分钟代表的兴趣程度是大于在最后看十分钟的,这就像你在很饿的时候,吃前面一个馒头的满足感是远大于吃了 4 个馒头之后再吃一个馒头的满足感的。
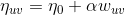
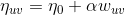
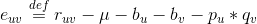
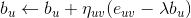
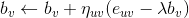
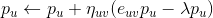
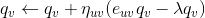
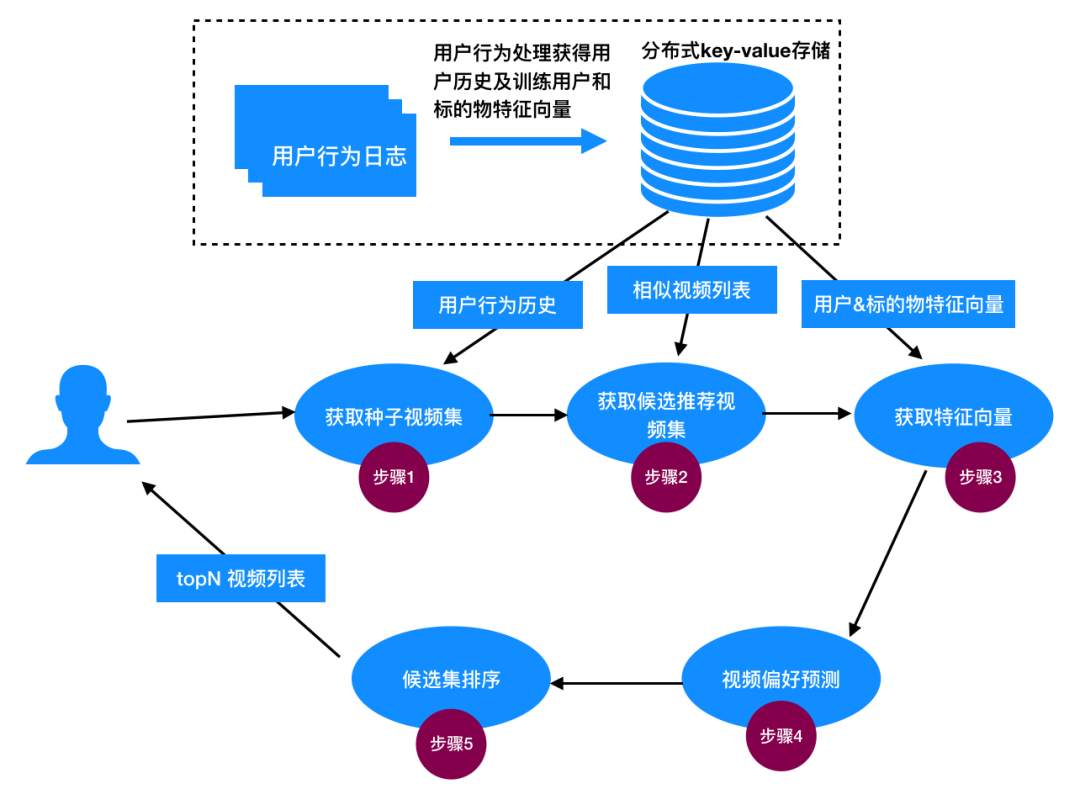
步骤 1:获取种子视频集
步骤 2:获取候选推荐视频集
步骤 3:获取特征向量
步骤 4:预测评分偏好
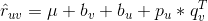
步骤 5:候选集排序
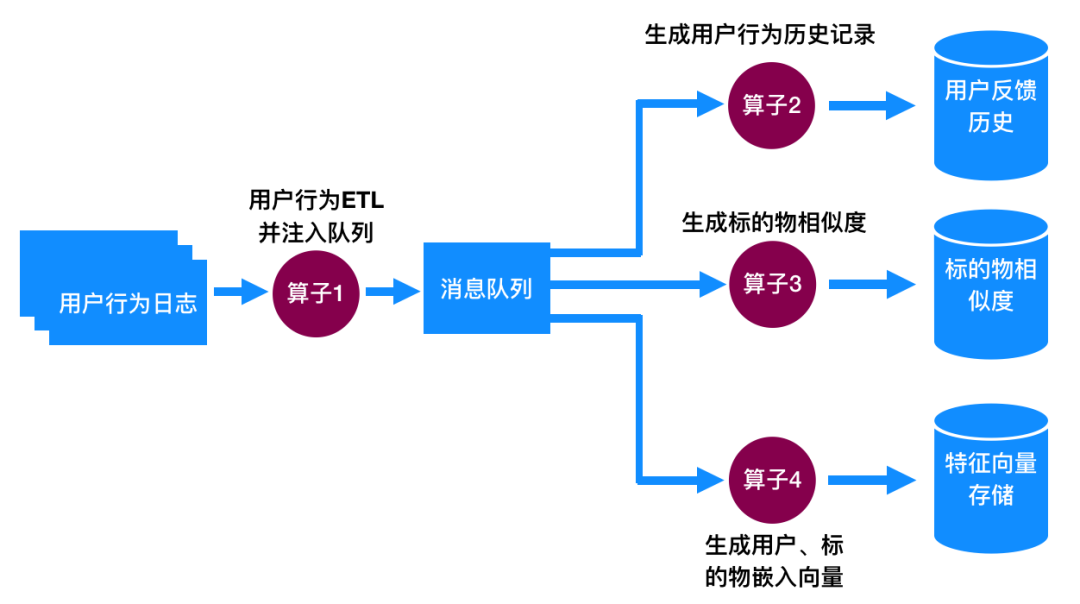 图5:计算个性化推荐依赖的用户播放历史、视频相似度、用户&视频特征向量
图5:计算个性化推荐依赖的用户播放历史、视频相似度、用户&视频特征向量
算子1:提取用户隐式反馈行为
算子2:生成用户反馈历史并存于分布式 key-value 存储中
算子3:计算视频之间的相似度
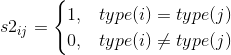
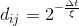 ,其中
,其中

算子4:生成用户和视频的特性向量
 图6:电视猫首页兴趣推荐:完全个性化推荐,每个用户推荐不一样的视频集
图6:电视猫首页兴趣推荐:完全个性化推荐,每个用户推荐不一样的视频集
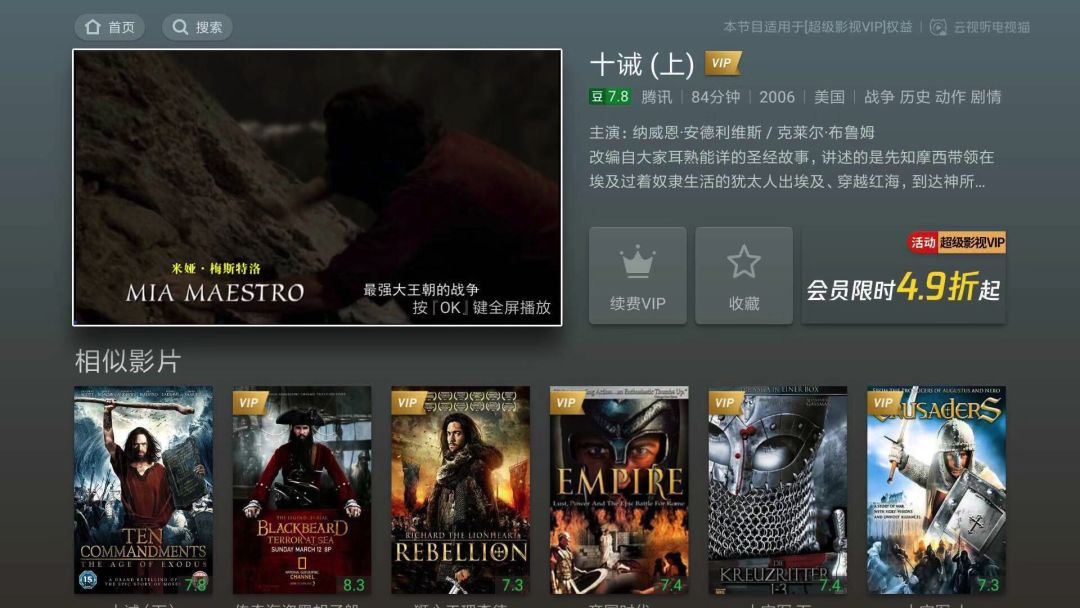 图7:电视猫详情页相似影片:视频关联视频的推荐,可以基于标的物特征向量来计算关联推荐
图7:电视猫详情页相似影片:视频关联视频的推荐,可以基于标的物特征向量来计算关联推荐
 图8:电视猫站点树个性化排序:基于群组个性化为用户做推荐
图8:电视猫站点树个性化排序:基于群组个性化为用户做推荐
(2) 推荐精准度不错
(3) 可以为用户推荐惊喜的标的物
(4) 易于并行化处理
(1) 存在冷启动问题
(2) 可解释性不强
-
Real-time Video Recommendation Exploration -
Real-Time Top-N Recommendation in Social Streams -
Online-updating regularized kernel matrix factorization models for large-scale recommender systems -
Factorization Meets the Item Embedding- Regularizing Matrix Factorization with Item Co-occurrence -
Collaborative Filtering for Implicit Feedback Datasets -
Large-Scale Parallel Collaborative Filtering for the Netflix Prize -
Content-boosted Matrix Factorization Techniques for Recommender Systems -
Matrix Factorization Techniques for Recommender Systems -
Metadata Embeddings for User and Item Cold-start Recommendations -
Neural Word Embedding as Implicit Matrix Factorization -
Collaborative Filtering with Temporal Dynamics -
Factorization Meets the Neighborhood: A Multifaceted Collaborative Filtering Model -
Scalable Collaborative Filtering with Jointly Derived Neighborhood Interpolation Weights -
Online collaborative flitering -
Online-updating regularized kernel matrix factorization models for large-scale recommender systems -
Fast incremental matrix factorization for recommendation with positive-only feedback -
Online personalized recommendation based on streaming implicit user feedbac
(*本文为 AI科技大本营转载文章,转载请联系作者)
◆
福利时刻
◆
入群参与每周抽奖~
扫码添加小助手,回复:大会,加入福利群,参与抽奖送礼!

推荐阅读
分析CVPR 2019论文关键词,我看到了计算机视觉的最新趋势 | 附代码
入门大爆炸式发展的深度学习,你先要了解这6个著名框架
用Python的算法工程师们,编码问题搞透彻了吗?
Python冷知识,不一样的技巧带给你不一样的乐趣

登录查看更多
相关内容
Arxiv
4+阅读 · 2019年3月7日
Arxiv
9+阅读 · 2018年5月30日