基于知识图谱和图卷积神经网络的应用和开发
本文概览:
1. 图卷积背景和基本框架
1.1 图算法介绍
我们都知道在数据结构中,图是一种基础且常用的结构。现实世界中许多场景可以抽象为一种图结构,如社交网络、交通网络、电商网站中用户与物品的关系等。
目前提到图算法一般指:
-
经典数据结构与算法层面的:最小生成树(Prim, Kruskal, ...),最短路(Dijkstra, Floyed, ...),拓扑排序,关键路径等; -
概率图模型:涉及图的表示、推断和学习; -
图神经网络 (Graph Neural Network, GNN):主要包含图表示学习(Graph Embedding)和图卷积网络(Graph Convolutional Network, GCN)。近年来,Graph Embedding和GCN成为网络数据分析与应用的热点研究问题。
1.2 深度学习介绍
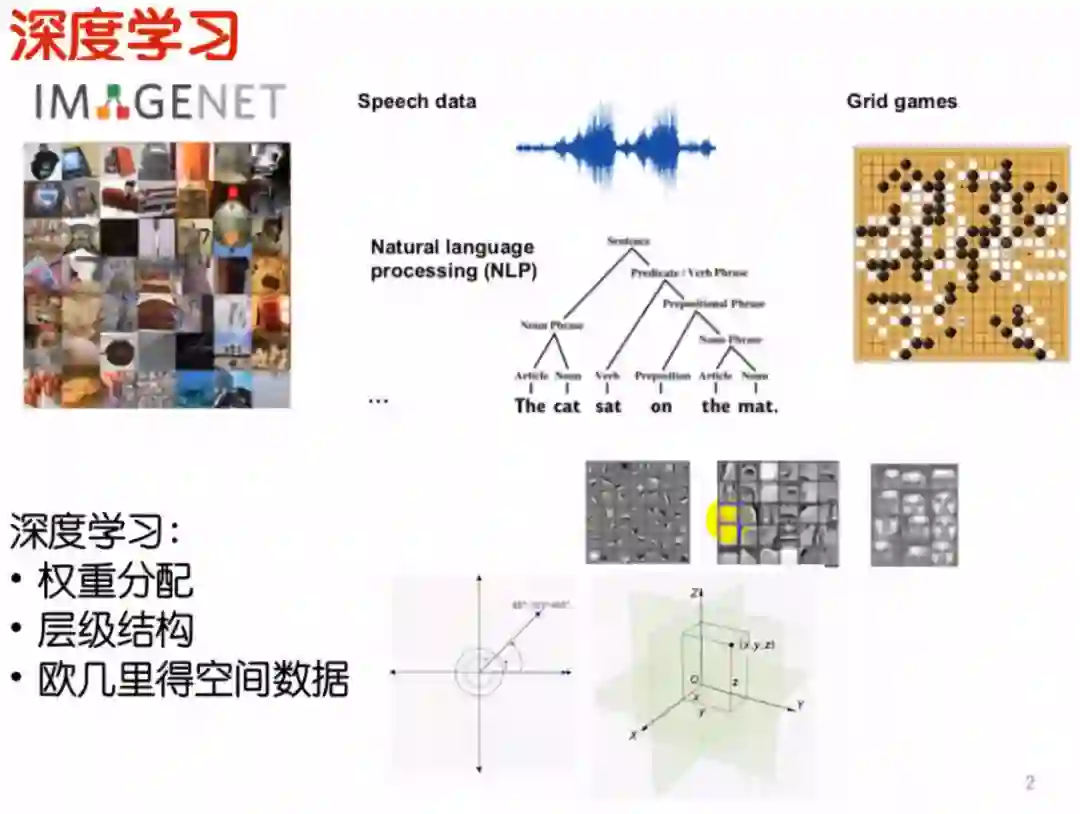
深度学习技术为计算机视觉(人脸识别)、语音识别、自然语言处理、强化学习(AlphaGo)等领域的发展做出了重要的贡献。深度学习作为一种如此重要的技术,主要有三个特点:
-
权重分配: 训练过程中有一个权重的分配,形成一个权重矩阵,在模型训练过程中学习得到权重矩阵; -
层级结构: 网络中每一层的结果都依赖于上一层网络,网络中信息是一层一层往下传递; -
欧几里得空间数据: 网络输入的数据是欧几里得空间数据。
什么叫欧几里得空间数据呢?我们在学习数学的过程中经常用一维坐标、二维坐标、三维坐标,甚至是用多维坐标来表示数据在哪一个位置上,表现数据之间的“距离”可以很容易在二维坐标中体现,表现数据的“立体结构”可以很容易在三维坐标中体现,这就是欧几里得空间数据。例如下图所示:图像是一个二维数据,用xy坐标就可以表示;语音数据就是一个一维数据,它是一个时间数据,随着时间的变化有相应的信息;自然语言处理也可以用一个二维坐标进行表示;围棋也是一个二维坐标。
1.3 图结构数据
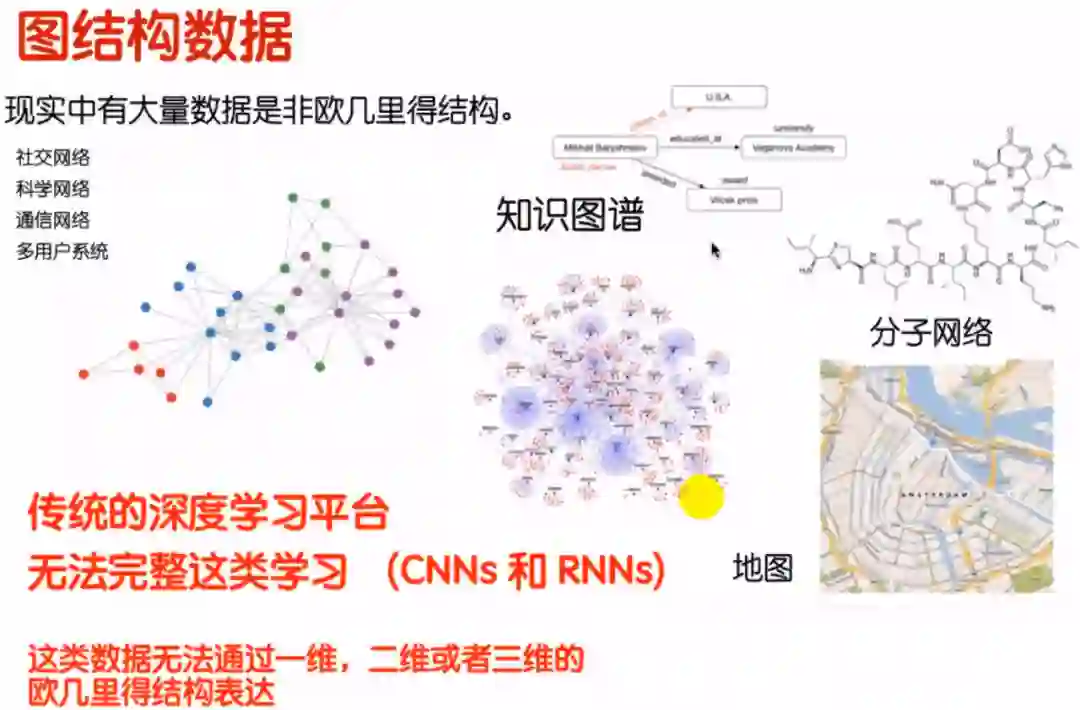
在深度学习处理的数据类型里面,大部分数据是能通过欧几里得空间进行一个转换,把数据投射到一个坐标轴里。但是在实际生活中,有很多数据不是能简简单单通过欧几里得结构进行表达的。比如在社交网络里,我们都会使用微信,人与人之间会通过微信加朋友,我们把每一个人当作节点,人与人之间形成的朋友关系当作边,这样就会形成一个图。在这个图里面,没有任何的距离信息,也没有任何的空间信息,这是一种非欧几里得的空间结构信息。那怎么对这种结构信息进行训练呢?在以往的深度学习模型中(比如CNNs、RNNs等)无法完成这类数据的学习,所以才出现了图卷积技术来解决这类数据的疑难问题。
现实生活中非欧几里得的数据有哪些呢?比如:
-
刚才说的社交网络; -
还有科学网络,科学家之间的网络,写了一篇论文,论文里有哪些作者,作者之间互相引用论文就会形成一个很大的引用论文的网络; -
通信网络,所有的无线通信设备、物联网都是通信网络; -
多用户系统,就是一个系统里面有很多用户,上面提到的社交、科学、通信三个网络都属于多用户系统网络; -
知识图谱,也是一个很大的图结构; -
分子网络,分子结构也能构成一个图; -
地图信息,地图中的每一个购物地点,也可以构成一个图的结构。
以上提到的这些例子,在深度学习里面用CNNs和RNNs来处理这些非欧几里得结构数据效果不是很好,所以我们提出了图卷积网络(Graph Convolutional Network,GCN)。
1.4 图卷积发展历史
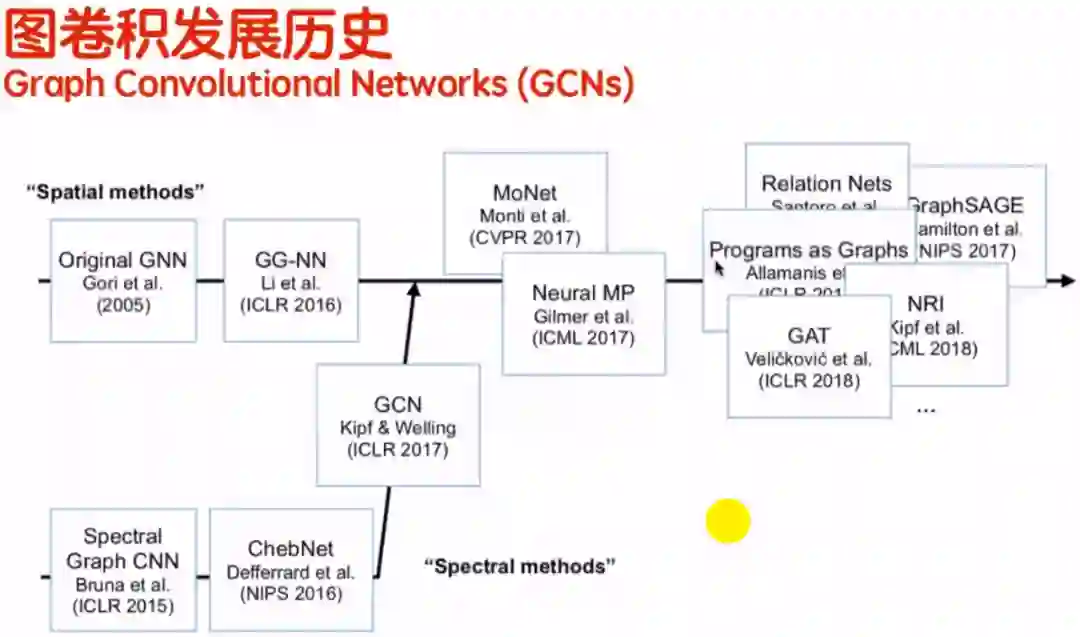
关于图卷积的发展历史,我们从两条线来讲。第一条线是“空间域”,也称为实域(Spatial methods),第二条线是“频域”(Spectral methods),频域和实域可以通过傅里叶变换相互转化。
在2005年的时候Gori等人提出了GCN的基本概念,由于1998的时候CNN刚被提出来,在2005的时候CNN是非常的火热,科学家并没有把重心放在GCN的基本概念上。经过十年的发展,提出CNN团队的科学家Bruna等人发现用现有网络不能很好的处理非欧几里得数据,因此提出GCN在频谱上的应用,把频谱上原始的实域数据转化到频谱上,然后做一个CNN深度学习卷积,发现效果不错。但是在2015年的时候,是缺乏理论支持的。直到2016年,相关的科学家Defferrard等人提出了一些理论的支持,解释了GCN为什么在分类上有好的结果,因为科学家从频谱上论证了GCN的可控性。同时在2016年,Li等人将GCN在实域过程中做了一个简单的应用,告诉大家GCN有一个很好的分类效果,但是也缺乏理论的解释。
直到2017年,Kipf & Welling等人的GCN文章横空出世,他们发现GCN把频域和实域两个域的数据通过数学公式的证明可以联系起来。之前的工作有一部分是通过频域来验证GCN的好坏,还有一部分工作是在实域上做一些尝试,发现GCN效果不错。Kipf & Welling等人的文章就解释了为什么GCN效果不错、GCN为什么可以处理实域上的数据,也提出了一些最简单、最基本的模型。随着Kipf & Welling等人文章的发表,在2018年的时候GCN受到了广大科研工作者的重视,然后大家就在这篇文章的基础上不断地创新和改进,提出各种各样的模型。
1.5 图概念回顾
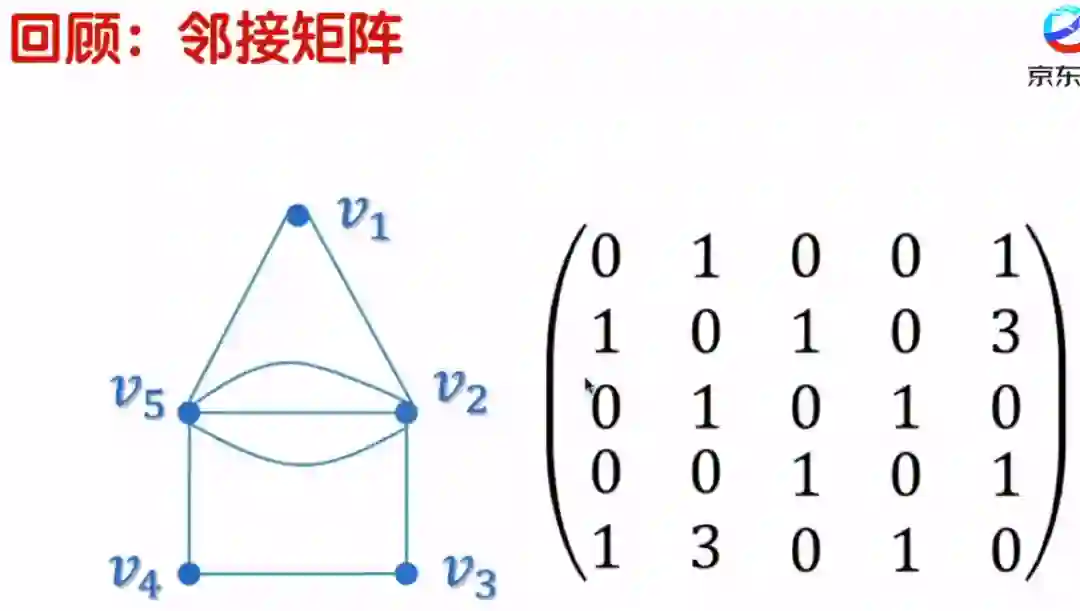
图是由若干顶点及边所构成的图形,图中可以无边,但至少包含一个顶点。
通常使用邻接矩阵来表示和存储图。对于一个含有 个顶点的图,采用一个大小为 的矩阵 存储图的结构。对于有权图, 可以表示 到 的边的权重;如果是无权图,则可设为 表示存在边, 表示不存在边,如果两个顶点有多条边,则 就是边数之和。因此邻接矩阵的表示相当的直观,而且对于查找某一条边是否存在、权重多少非常快。但其比较浪费空间,对稠密图来说,会比较适合。
邻接矩阵对角线上元素都是 ,上三角矩阵和下三角矩阵以对角线而对称。在图的实际应用中,只看上三角或下三角就可以了。
1.6 图卷积基本框架
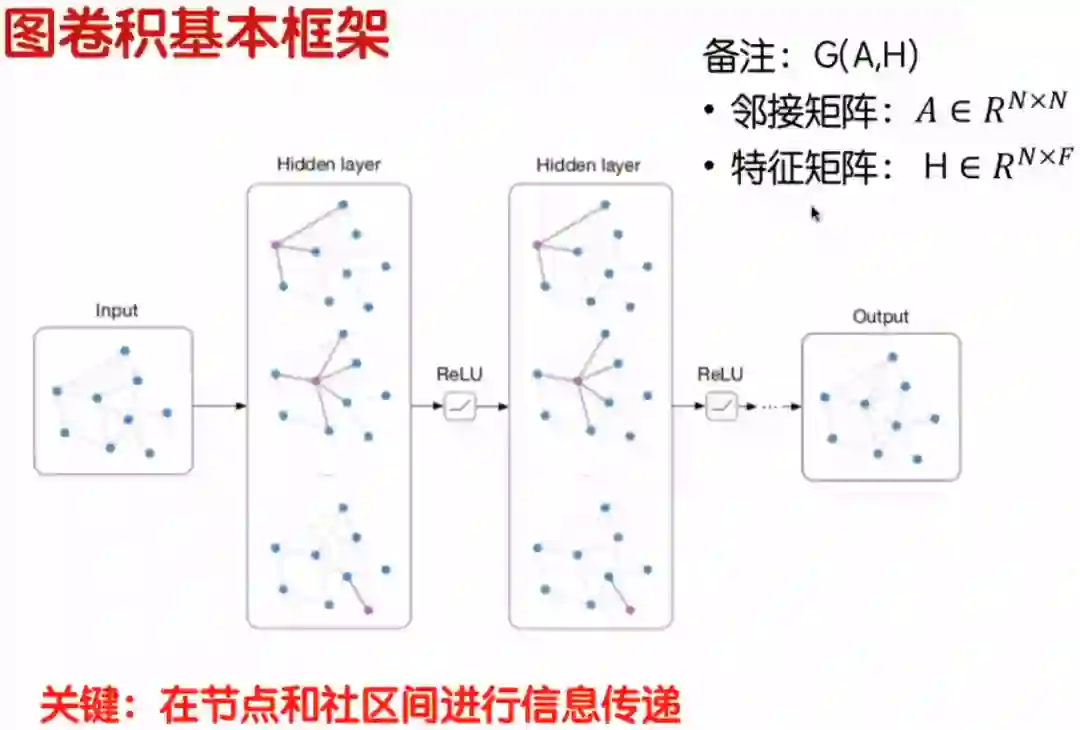
图卷积的核心基本框架包括两个矩阵:(1)一个是邻接矩阵 ,有 个节点,矩阵 的维度就是 ;(2)另一个是特征矩阵 ,矩阵H的维度为 ,其中 代表图中节点的个数, 为每个节点的特征维度。比如,我们每个人在社交网络中都是一个节点,但是我们的性别、年龄、籍贯等信息就是我们的特征。
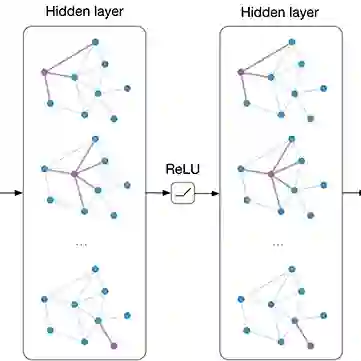
在图卷积基本框架中,输入层输入的是邻接矩阵,在隐藏层把特征矩阵点乘到每一个节点上进行训练,网络每次更新都是更新特征矩阵,图结构是不变的,经过多次训练以后,特征矩阵达到收敛的情况(也就是特征矩阵中值基本不变),最后再做一个分类,给出概率,判断图中节点属于哪一类。在整个网络训练过程中,把节点和特征做了一个点乘,实现了节点和特征在社区间的传递。
下面,给大家介绍一下GCN的数学概念,主要包含GCN的特征信息如何跟节点点乘结合在一起,一层一层往下传递进行训练的。
1.7 卷积神经网络回顾
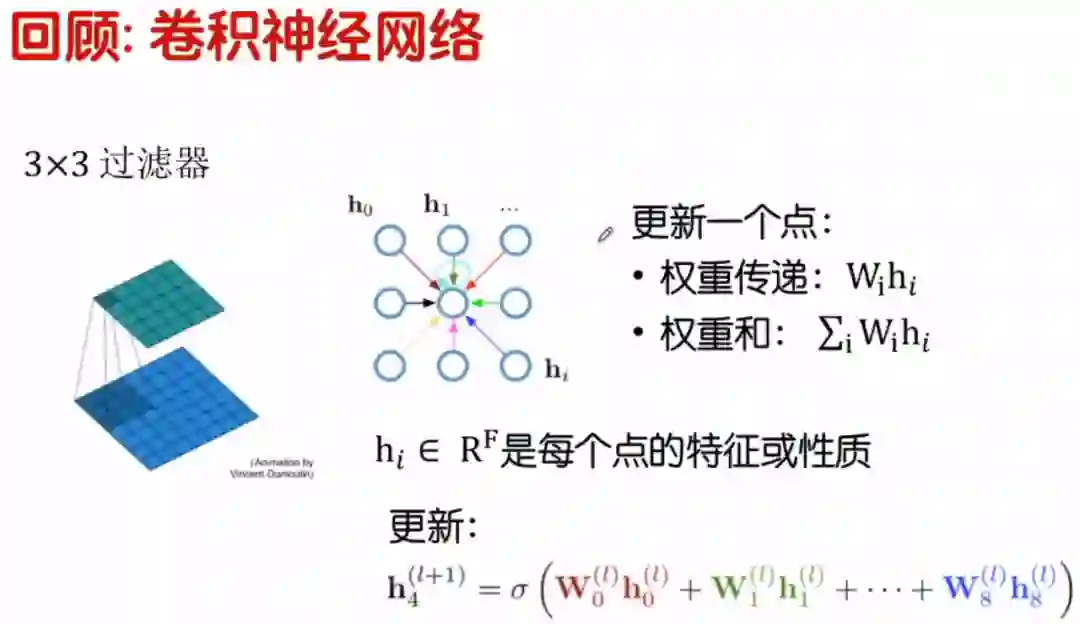
在卷积神经网络中,上一层输出的特征图与过滤器进行卷积操作,即输入项与过滤器之间进行点积运算,然后将结果送入激活函数,就可以得到输出特征图。下图展示的是过滤器对输入特征图的一次卷积操作,公式如下图中所示。
1.8 图卷积
卷积神经网络的前向传播公式为:
图卷积的前向传播公式为:
对比图卷积网络与卷积神经网络的前向传播公式可以发现,图卷积网络加入了邻接矩阵的信息。如下图所示,计算更新红点,就是以它周边相邻的四个点来更新它自己,不需要把不相邻的节点信息更新过来。
上面的公式接着往下推导就是,邻接矩阵 点乘特征矩阵 再点乘权重矩阵,经过激活函数然后更新到下一层的特征矩阵 中,直到 基本没有变化的时候,就可以停止更新。
在上述步骤中会有几个问题:
-
如果只用邻接矩阵的话,由于邻接矩阵中节点自身没有环,对角线上的元素都为 ,在训练的过程中不能考虑自身的信息; -
邻接矩阵 没有归一化,可能导致度大的节点,具有更大的特征值,影响特征提取,模型收敛。
为了解决以上问题,进行了拉普拉斯的变化,对上式做进一步改进。 为图的度矩阵, 为图的邻接矩阵,进行 的操作,解决对角线的问题,使训练中涵盖了自身节点的信息。公式如下:
然后再解决归一化的处理,下面两个式子都是拉普拉斯归一化处理:
归一化处理的主要目的是,希望这些特征值更加均匀化,不需要特别大的特征值,导致最终影响特征提取和模型训练。大部分会选择第一个式子作为归一化处理,因为它训练出来的矩阵是对称的,另外矩阵的每一列相加的值为 。
1.9 图卷积的演示
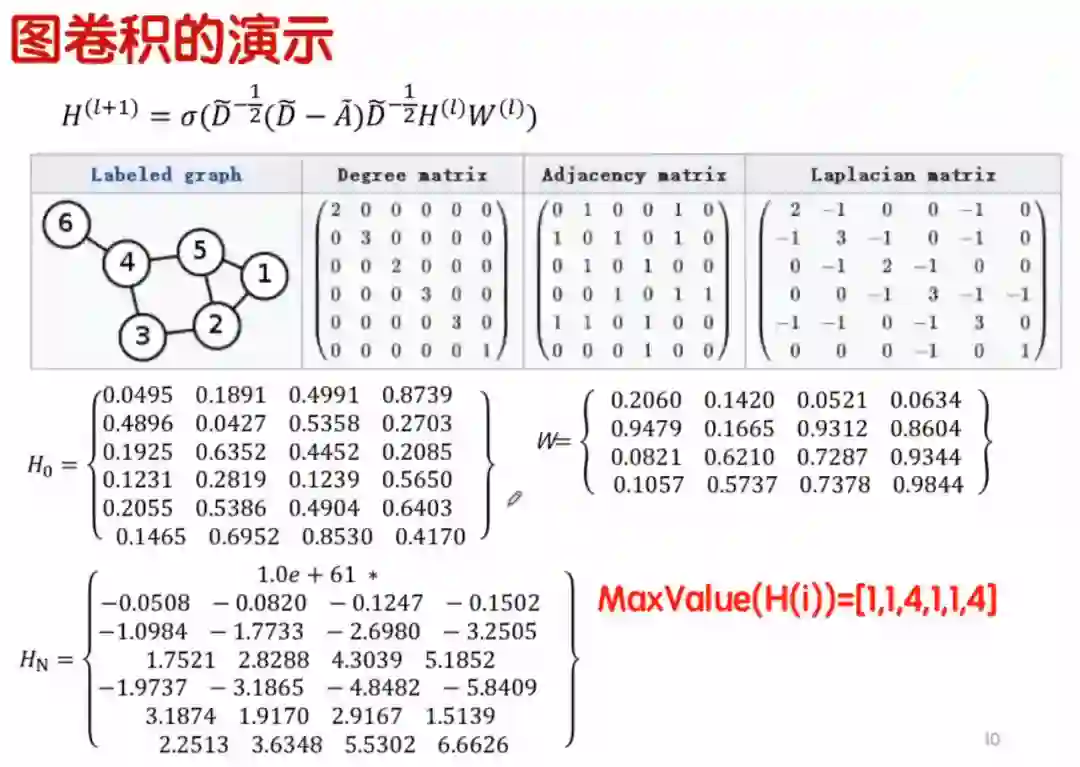
上图中一共有六个节点,邻接矩阵中
节点和
节点有边,相应位置值为
,
节点和
节点也有边,相应位置为
。度矩阵就是只有对角线有值,该值是对应节点有多少条边,
节点有两条边,
节点有三条边。度矩阵减去邻接矩阵就变成了拉普拉斯矩阵了。然后,在下式中对度矩阵求逆开根号,然后乘以拉普拉斯矩阵,最后不断的更新
。
在这个例子中, 没有给定,我们随机出一个 ,它是一个 的矩阵, 也是一个随机出的矩阵。在GCN的卷积过程中,权重 不像CNN中那么重要,很多时候我们在做GCN卷积的时候, 权重就是随机产生的。经过多次循环训练,得到一个 收敛的情况,特征矩阵就是 这样的值。然后在求 中每一列的最大值,再进行列数的分类,我们可以发现第 、 、 、 个节点分类是 ,第 、 个节点分类是 。GCN可以很好地把图的结构,分成了两类, 、 、 这三个节点在图论里面是全连接图,那这三个节点很相似;第 、 节点都有三条边,所以把 也分到了 、 、 对应的类别中; 和 自然而然就没有和其他节点关系那么密切,就把 和 分到另一类中。
这个例子中想给大家突出两点,第一点就是随机产生了特征矩阵,依据图的拓扑结构,就能得到一个很好的分类效果;第二点就是通过这个例子把抽象的理论具体化,大家就能看懂这个矩阵 是怎么计算的。
图卷积的核心就是更新 这个公式,那么在图卷积的应用和开发过程中两个核心的创新是特征矩阵和邻接矩阵。
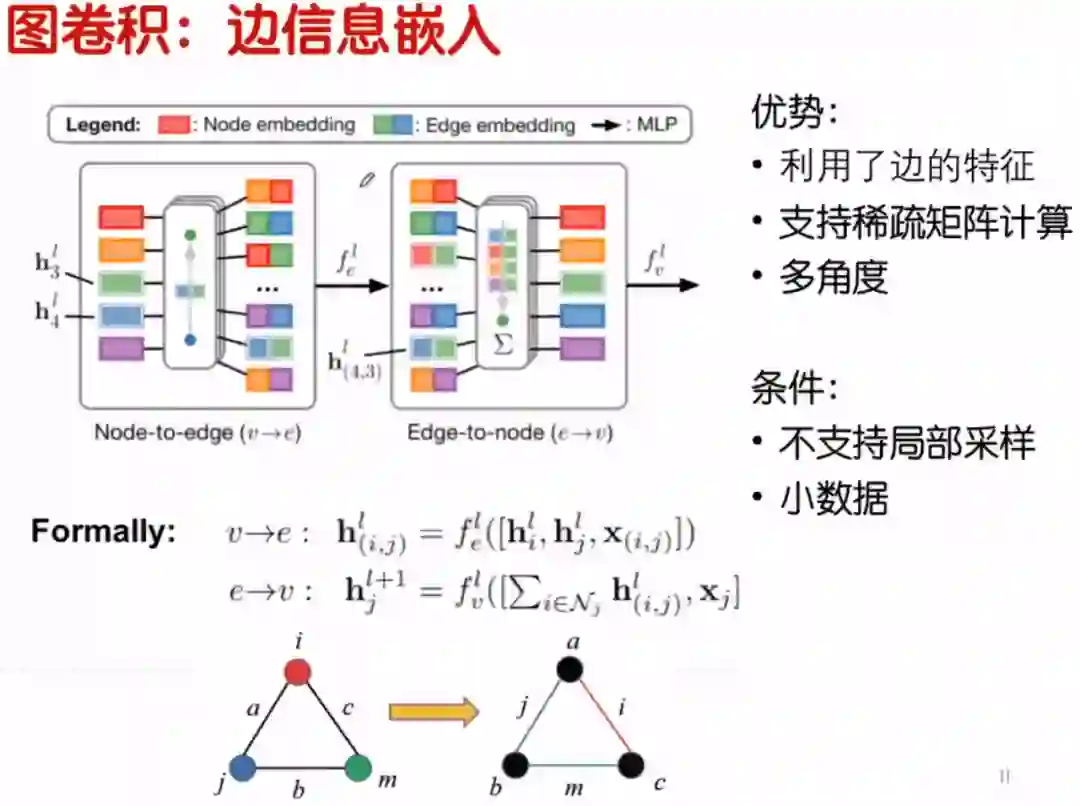
1.10 图卷积:边信息嵌入
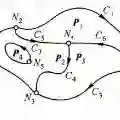
在图的拓扑结构中,有时边是有权重的,如果这个权重值单单放在邻接矩阵中(也就是权重信息放在点里),仅仅有邻接矩阵的乘积并不能突显出边的信息。如果要把边的信息考虑进图卷积中,我们可以把圆图转为线图。如下图所示,圆图有 、 、 三个点,边是 、 、 ,转换后就是把边看成点,点看成边。因为边里面也有特征信息,这个时候进行两次的图卷积的迭代和循环,能很好的把边的信息整合进去了。训练的过程是一样的,重要的是如何把圆图转换成线图。这样做的优势是把边的信息考虑进去,支持稀疏矩阵的计算,从多角度考虑(即考虑了边,又考虑了点)。条件的局限性是,由于边转成点,点转成边这样计算的复杂度还是挺大的,现阶段是只能处理小数据。
1.11 半监督图分类
举个半监督图分类的例子。下图中有一个图,我们设定黑色圆圈的点已经知道分类了,其它的点并不知道它们的分类,那我们如何进行一个分类呢?在这个过程中,我们用了一个损失函数:
其中, 是已分类的节点集合, 是分类矩阵, 是GCN输出的结果。
有了半监督图分类的损失函数后,我们来看一下如何用代码实现。下图展示了部分核心代码。
我们在来看一下,实验的结果。从下图中,可以看到GCN把未分类的点分的很开。
1.12 图卷积:科学家网络
我们在看一个科学家网络的例子。在科学家网络中,我们每写一篇论文都有题目,互相引用论文就会形成一个关系,任务是给你这些论文的题目,想预测一下论文的类别,比如这篇论文是属于物理、化学还是数学。如下图展示,只用到了两层GCN,用GCN的方法比之前的结果有很大的提高。
2. 基于知识图谱的图卷积
2.1 知识图谱
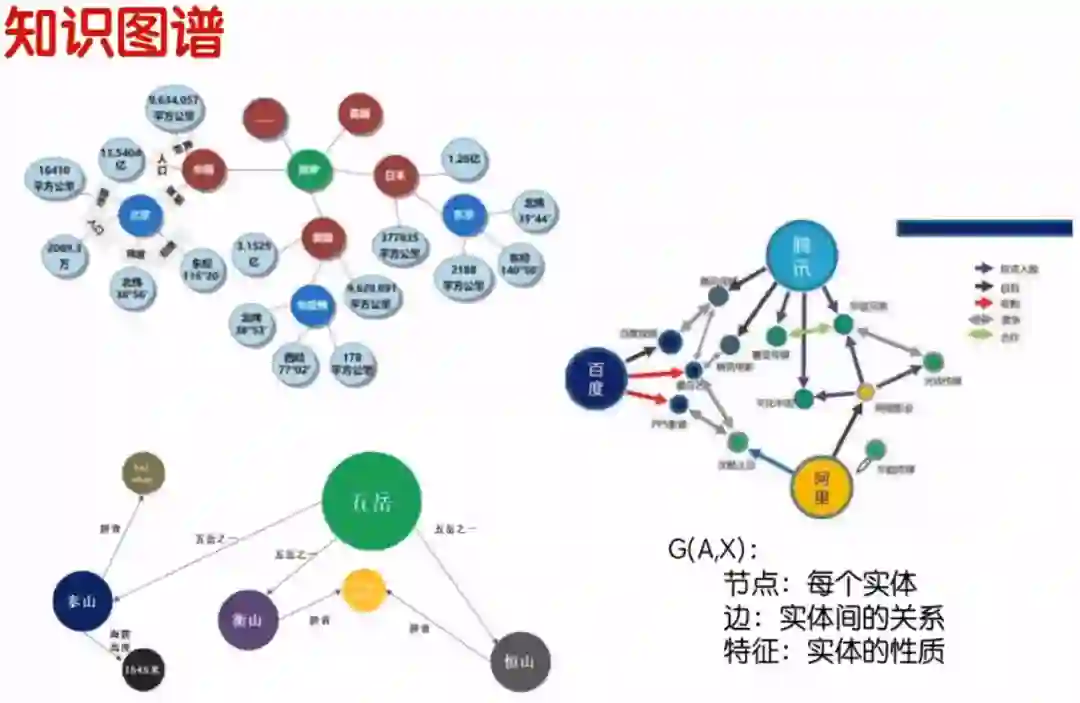
下图展示了关于知识图谱的三个例子。来看一下第一个例子,关于国家我们能想到中国、美国、日本等。中国有哪些属性呢?中国的面积是 平方公里,人口有 亿,中国的首都是北京等。就是我们在搜索一个关键词的时候,它相应出来的一些东西就会形成知识图谱。比如我搜索中国,可能出现美国、日本、英国等。在知识图谱中,我们可以认为图中节点是国家、中国、北京这些是实体,边就是实体间的关系,比如中国和国家有什么关系,特征就是实体的性质。
2.2 图卷积:知识图谱
我们现在的数据有:用户,比如我们现在听课的 千多个人都是用户;我们有一些实体,比如电影、书籍、音乐、食物等;还有用户对哪些电影感兴趣、喜欢看哪些书籍等,就是用户 与实体 有联系,比如Microstrong对教父这个电影很感兴趣,那么 ;关系的话,就是每个实体之间会有一个关系,电影到教父会有一条边;最后还有一个特征矩阵 。图卷积的公式如下图所示。
我们现在把实体的关系嵌入到图中,那怎么把实体推荐给用户呢?我们针对每个用户在新建一个图 ,就是用户对实体之间关系的重要性。就是把实体矩阵 变成一个有权重的矩阵,然后每一个用户有一个邻接矩阵,然后针对每一个用户的邻接矩阵进行训练。上图中的圆圈三就是简单基本的图卷积过程。上图中的圆圈四就是做了一个标签顺滑的过程。
标签顺滑现在在CNN中也是用的很多,为了在训练过程中提高模型的精度,做了一个标签顺滑。举例,以前在训练深度模型的时候,随着训练的不断迭代,模型对训练的结果更加自信,它认为一个动物是猫、或者是狗,模型能很自信的确认这个动物是猫或是狗,它的预测值是实值 或者 。但是在训练过程中由于模型过于自信,可能会导致更多的误差,当我们把 改成 , 改成 ,调整一下标签顺滑的值,最后模型预测的结果会更加的好。基本我们现在做的大部分深度神经模型,都会用到标签顺滑这样的技术。
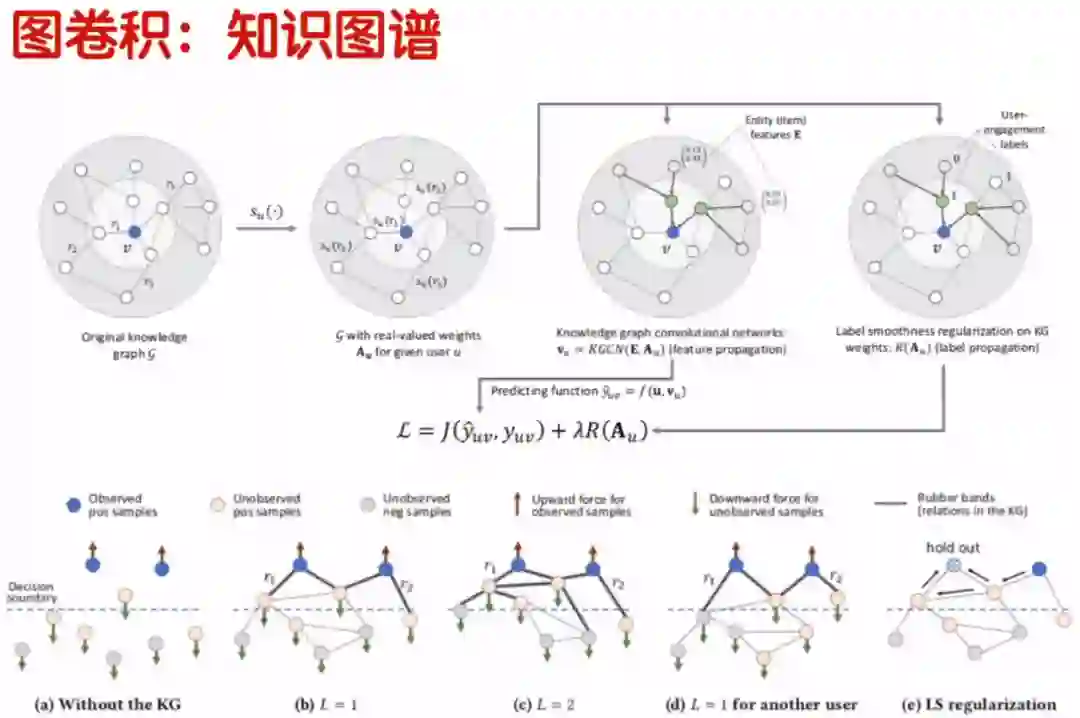
上图第一个圆圈是:新建了一个知识图谱。第二个圆圈是:用户对每一个实体感兴趣的东西,新建一个权重的矩阵。第三个圆圈是:对第二个圆圈的图进行图卷积。第四个圆圈是:在GCN中运用标签顺滑的技术。损失函数定义为:
其中, 是图卷积的损失函数, 是标签顺滑正则。
我们再来说一下,GCN的基本训练过程。上图中(a)表示,没有考虑知识图谱的结构,蓝色的点是用户感兴趣的实体;粉色的点是用户没有观察到,但是比较感兴趣的点;灰色的点也是用户没有观察到的点,但是是用户不感兴趣的点。现在我们的目的是通过训练把粉色的点推荐给用户,让用户进行选择,灰色的点不推荐给用户。(b)表示,经过第一层GCN的训练把虚线上的两个粉色点推荐出来了。(c)表示,经过第二层GCN的训练把虚线上的三个粉色点推荐给用户了。有误差的情况下,把用户不感兴趣的灰色点也推荐给用户了。(d)图是针对其他用户,上面讲的(a)、(b)、(c)是对用户 来说,(d)是针对用户 ,针对用户 模型训练出来的结果并不适用。(e)表示,加了标签顺滑以后,模型推荐出的点更加精准。
2.3 标签顺滑
我们来了解一下标签顺滑正则的函数。标签顺滑一共有三步:能量方程、最小值、交叉熵。能量方程中 ,就是用户 对 这个实体是否感兴趣,感兴趣这个值为 ,不感兴趣这个值为 。进行一个能量方程的处理,把相同的label给去掉,不同的label保留下来。然后取最小值,最后做一个交叉熵。交叉熵里面用到了KL距离函数,它表示两个概率分布越相似,值越小。
2.4 知识图谱:伪代码
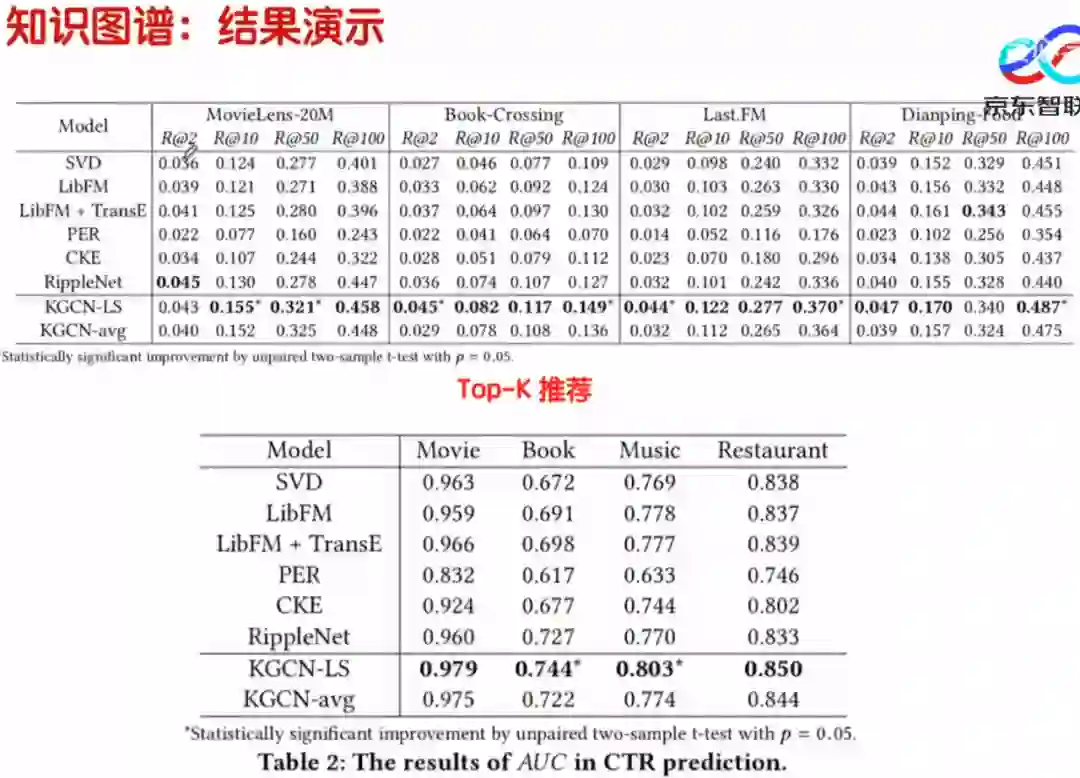
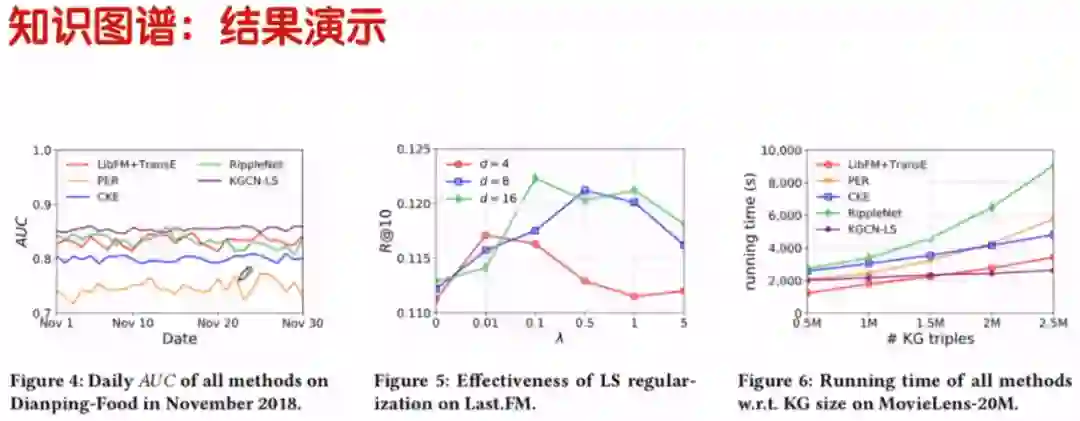
2.5 知识图谱:结果演示
上图展示了图卷积在知识图谱上应用在推荐方面的一个例子, 可以看到GCN相比其它推荐算法,还是有一定的结果上提升的。
上图从准确度、速度和效果上展示了,GCN在知识图谱上的显著提高。
3. 研究方向
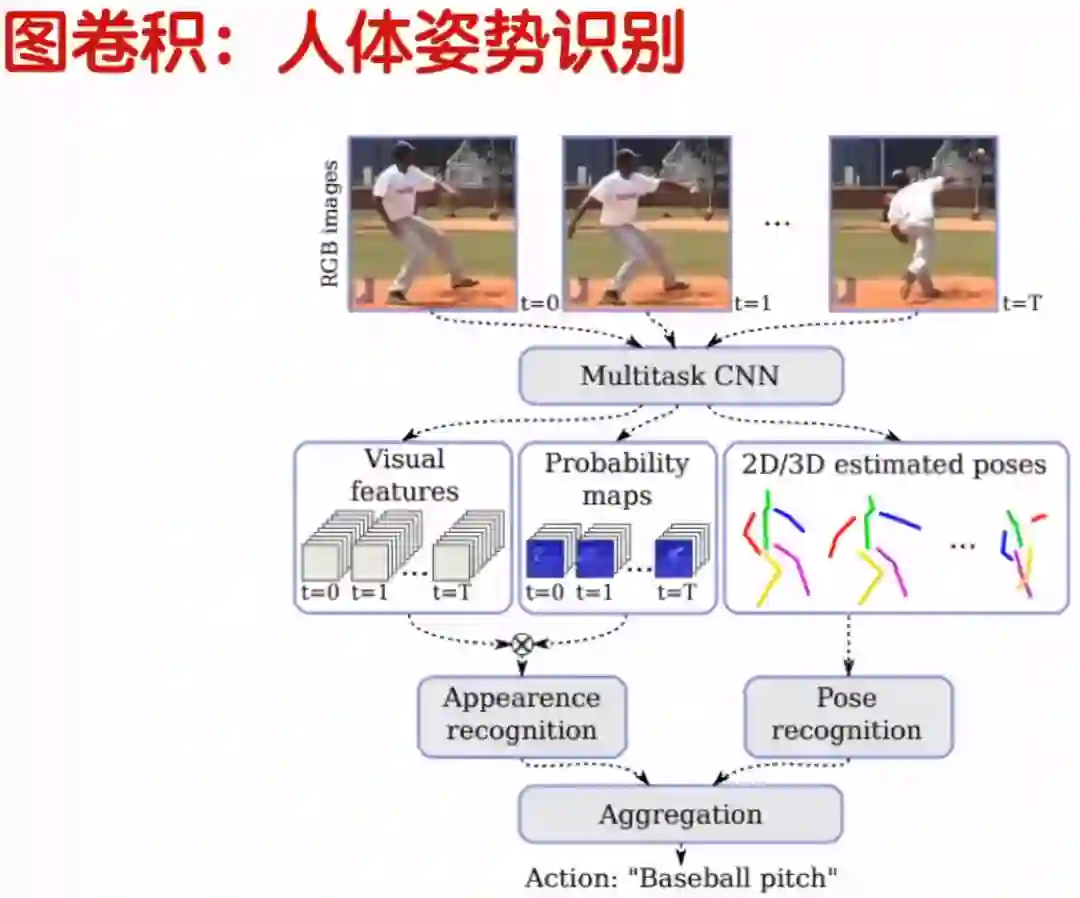
3.1 图卷积:人体姿势识别
人体的每一个关节点相当于图中的节点,骨骼相当于图的边。人体就是一个很好的图,聚类性也有,并且做每个动作,关节点的位置也是不一样的,这就可以很好的构建一个聚类性的图,然后进行训练。
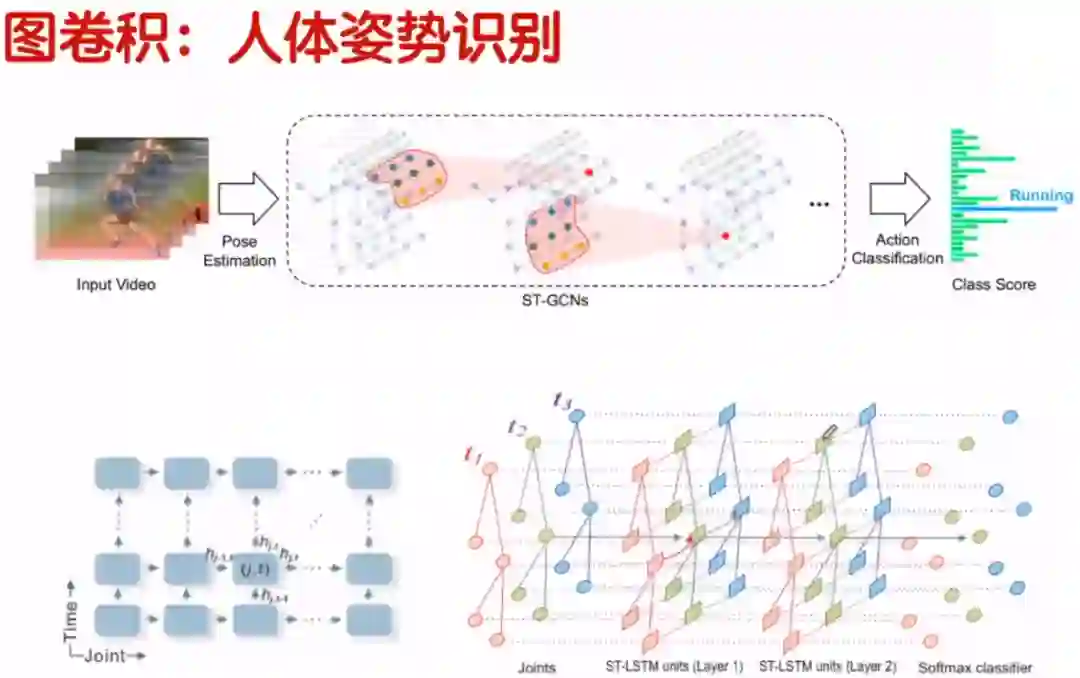
如下图所示,输入了一个视频信号,视频信号上有时间序列,每一个时间序列上就是一张图片。针对每一张图片,我们可以构建骨骼图,然后通过时间顺序找到每一个节点的位置把它们连接起来,然后就变成了一张大的图,把这个大的图放到GCN里面进行训练,最后到一个分类器里面,预测分类结果。下图的分类结果是跑步。
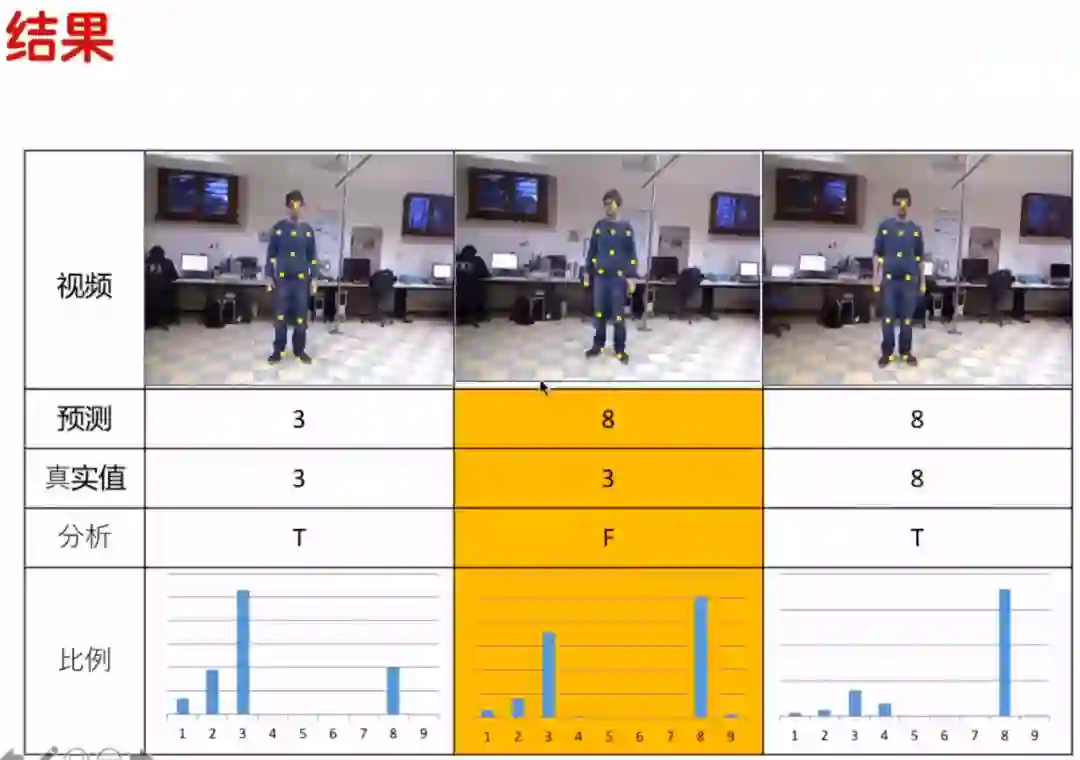
我们来看一下,GCN在人体姿势识别上的结果。
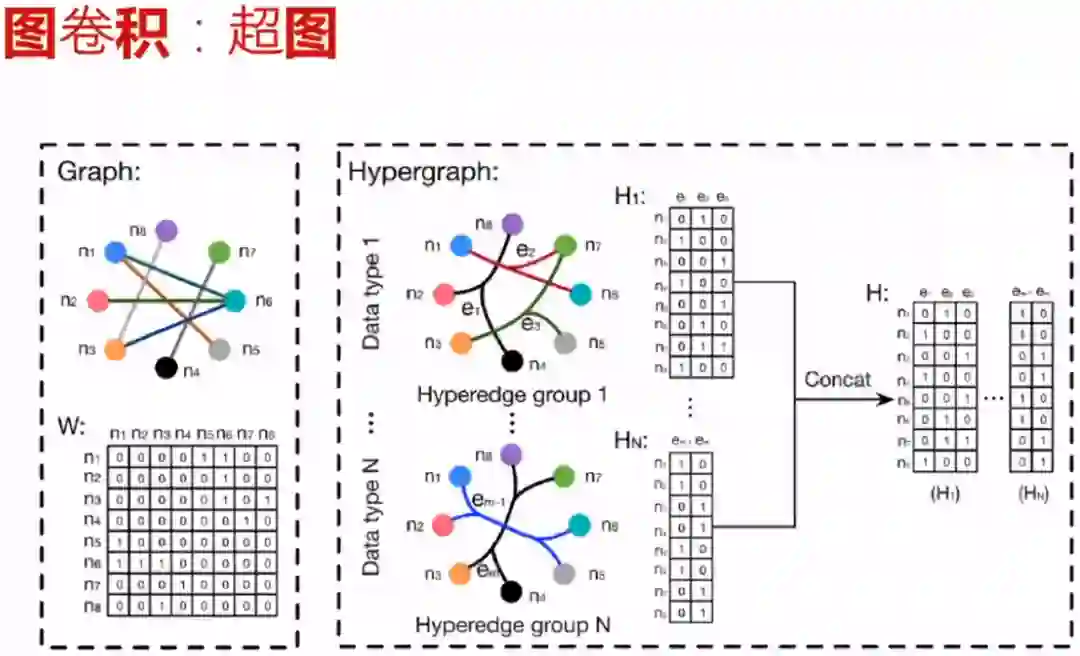
3.2 图卷积:超图
超图是图的一个基本概念。如下图所示,有八个点,把每个点选出来,可以有很多种的排列组合。我们选一个点,那总共有八个点可选择,就有八种排列组合。我们选两个点,比如 、 ,那 、 会构成一个子图。所以超图就是在有 个节点情况下,进行排列组合的问题。
3.3 图构建
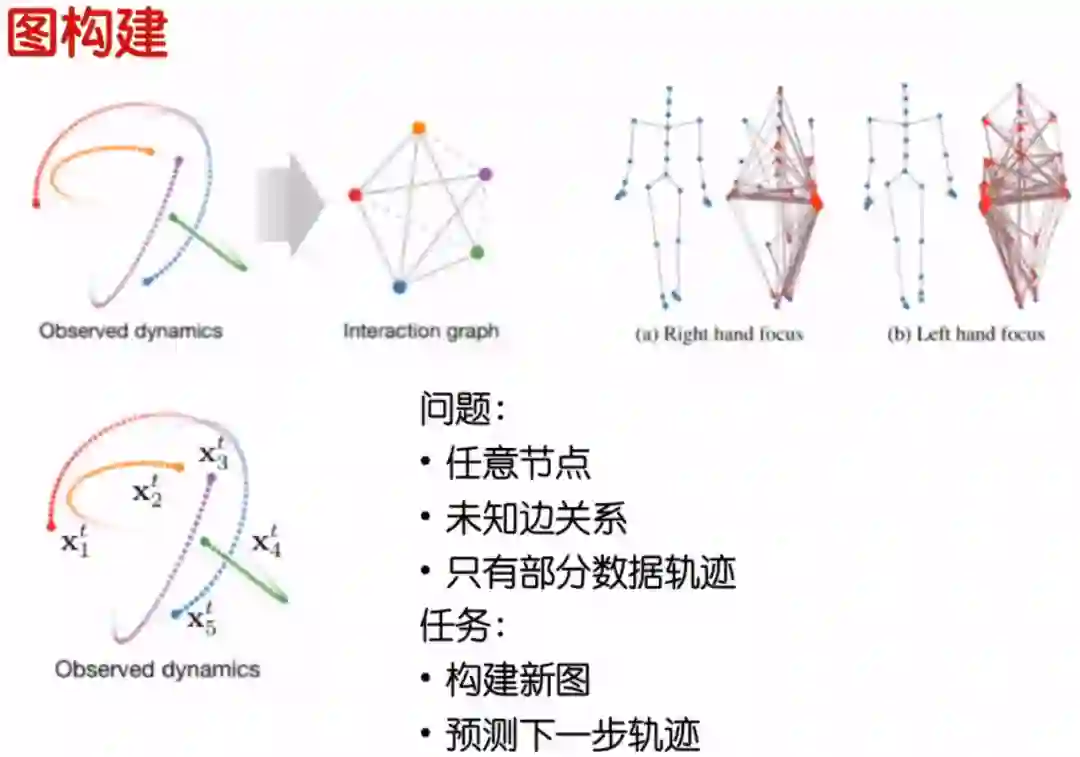
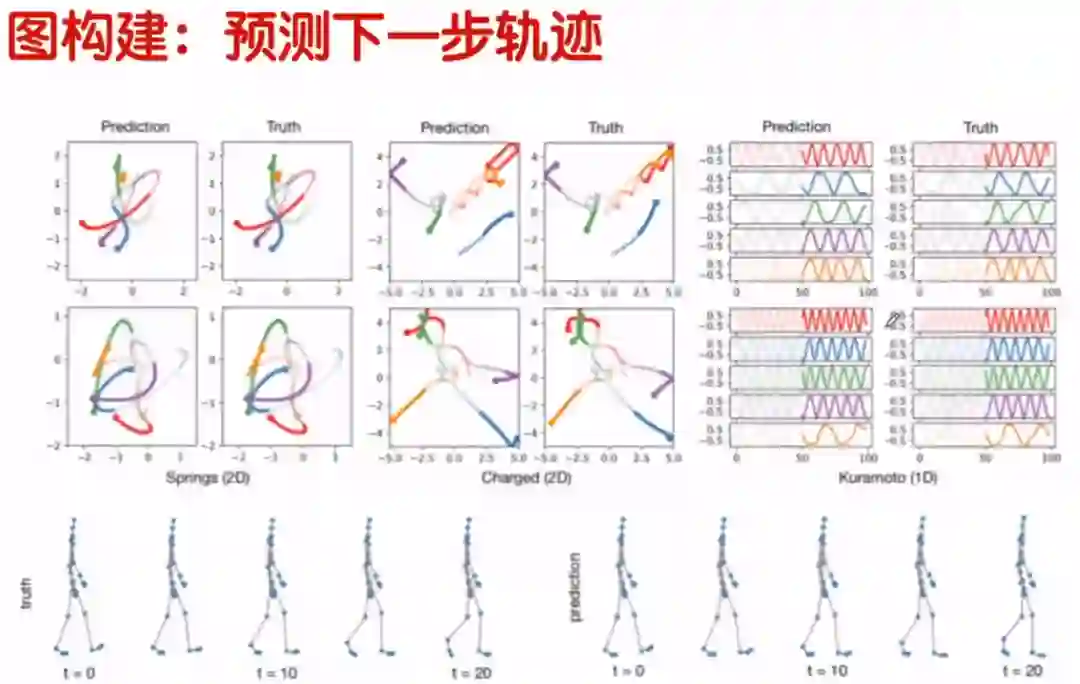
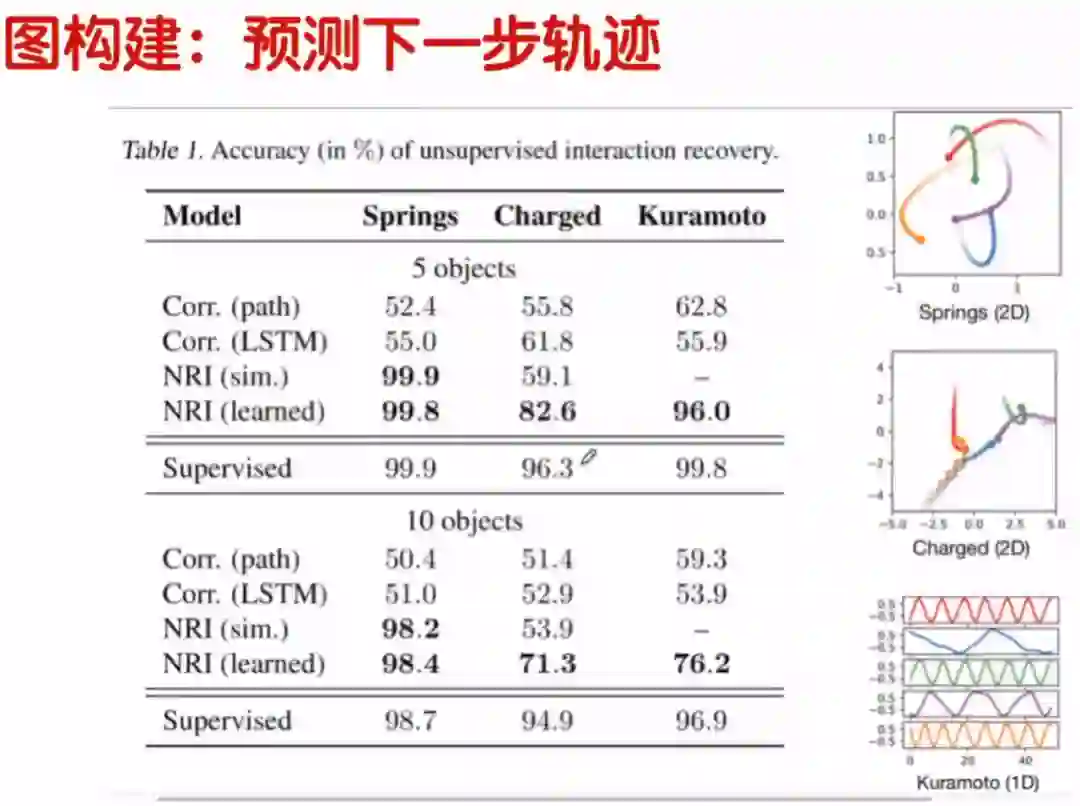
图构建问题就是,给一大堆数据,我们不知道数据之间有没有关系,我们怎么新建这幅图。新建完这幅图后,把图放到GCN里面训练,然后进行分类。
我们来看一个上图中左下角所展示的例子,一共有五个分子的运动图,分子之间是否有连续,分子之间位置和边的联系也不清楚,我们需要新建一个图,然后预测分子轨迹下一步动作。
上图中右上角所展示的例子,人体的动作,在每一帧新建图的过程中,图是以哪个节点为重心进行构建。比如,是以右手为重心还是以左手为重心。
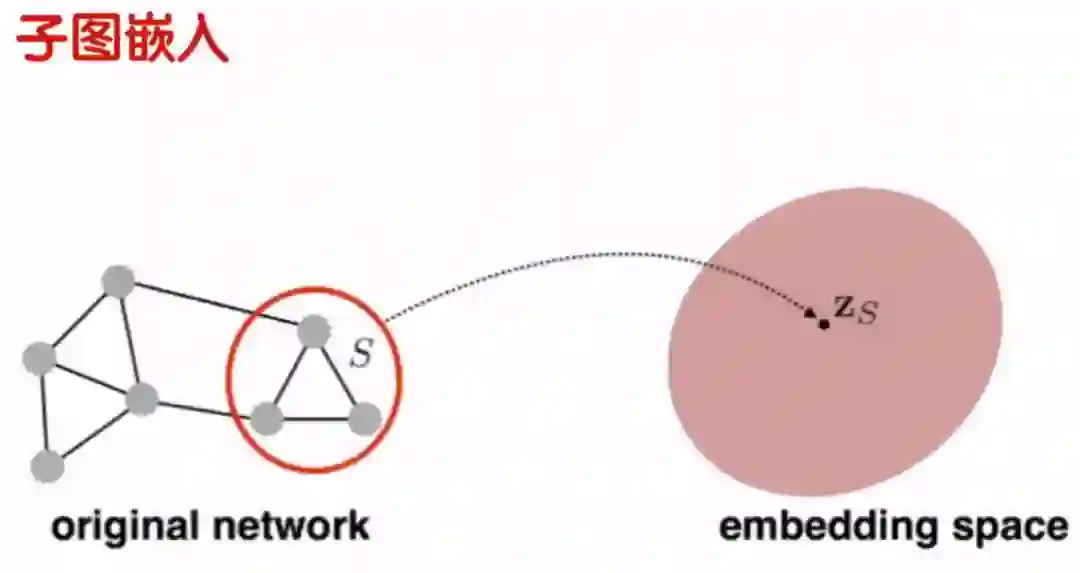
3.4 子图嵌入
图里面经常会考虑单个点,那我们把下图中的三个点考虑成一个点,放到GCN里面,结果会如何呢?这也是现在非常火的研究方向。
4. 场景应用
4.1 用户推荐系统
淘宝、Google、Facebook等公司在搜索和推荐过程中都用到了GCN的技术。
4.2 舆情监控和控制
各个国家和各个机构都非常需要舆情监控和控制,判断真消息和假消息,以及追踪消息的来源。GCN在舆情监控和控制中也是一个非常好的技术。
4.3 自动驾驶
每一部车子都有车载系统,车载系统都需要联网,这样就构建了一个非常大的图,也就可以应用GCN技术在图里进行推荐和用户筛选。这也是未来在物联网方面非常火的一个方向。
5. 总结
本文提到的所有知识点大部分来源于以下论文:
-
Knowledge Graph Convolutional Networks for Recommender Systems; -
Knowledge Graph Convolutional Networks for Recommender Systems with Label Smoothness Regularization; -
Graph Convolutional Neural Networks for Web-Scale Recommender Systems; -
Modeling Relational Data with Graph Convolutional Networks; -
SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS; -
COMPOSITION-BASED MULTI-RELATIONAL GRAPH CONVOLUTIONAL NETWORKS; -
Neural Relational Inference for Interacting Systems; -
Graph Convolutional Networks for Text Classification;
最后,给大家补充一下关于机器学习、深度学习的一些顶会知识:
-
机器学习、深度学习偏理论的顶会:NIPS、ICML、ICLR。 -
计算机视觉方向的顶会:CVPR、ECCV、ICCV。
6. Reference
本文是Microstrong在观看杨栋在B站上讲解的直播课程《基于知识图谱和图卷积神经网络的应用和开发》的笔记。直播地址:https://live.bilibili.com/11869202 。贪心科技官网已上线公开课回放,地址:https://www.greedyai.com/course/139 。
【1】概率图模型(PGM)有必要系统地学习一下吗?- 知乎 https://www.zhihu.com/question/23255632
【2】【Graph Embedding】DeepWalk:算法原理,实现和应用 - 浅梦的文章 - 知乎 https://zhuanlan.zhihu.com/p/56380812
【3】【NLP系列直播】 图卷积神经网络,BERT,知识图谱,对话生成,贪心学院,地址:https://www.bilibili.com/video/BV1bK4y1t7Pw?p=1
【4】基于知识图谱和图卷积神经网络的应用和开发,地址:https://www.bilibili.com/video/BV1ni4y1s7F6?from=search&seid=1051972300125641379
【5】贪心学院公开课-基于知识图谱和图卷积神经网络的应用和开发-杨栋,地址:https://www.bilibili.com/video/BV1HK411s7zp?from=search&seid=3179677231592653459
【6】图神经网络在线研讨会2020丨图表示学习和图神经网络的最新理论进展和应用探索,地址:https://www.bilibili.com/video/bv1zp4y117bB/
【7】图表示学习极简教程 - 他们都叫我0号的文章 - 知乎 https://zhuanlan.zhihu.com/p/112295277
【8】图卷积网络(GCN)的谱分析 - 他们都叫我0号的文章 - 知乎 https://zhuanlan.zhihu.com/p/124727955
【9】浅析图卷积神经网络 - GEETEST极验的文章 - 知乎 https://zhuanlan.zhihu.com/p/37091549
推荐阅读
文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化
斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用
太赞了!Springer面向公众开放电子书籍,附65本数学、编程、机器学习、深度学习、数据挖掘、数据科学等书籍链接及打包下载
数学之美中盛赞的 Michael Collins 教授,他的NLP课程要不要收藏?
模型压缩实践系列之——bert-of-theseus,一个非常亲民的bert压缩方法
关于AINLP
AINLP 是一个有趣有AI的自然语言处理社区,专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享,主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等,欢迎关注!加技术交流群请添加AINLPer(id:ainlper),备注工作/研究方向+加群目的。
阅读至此了,点个在看吧👇