针对初学者的图论速成

作者：Aaron Lelevier

编译：Bing

编者按：图论是数学里十分重要的学科，其以图为研究对象，通常用来描述某些事物之间的某种特定关系。我们都知道机器学习里的决策树，它可以表示特定特征条件下类的条件概率分布。而通常决策树的学习又包括了特征的选择、决策树的生成和决策树的剪枝。这种树形只是图的一个小分支，本文作者Aaron Lelevier将带你了解图论的基本理念，希望对你有帮助。

这篇博文的目标是总结我在图论学习中的要点。最初我想做这项研究是进入Neo4j之前，Neo4j是使用最广泛的图形数据库。我喜欢在做某件事时学到新的知识，所以这次学习过程让我受益良多。

在写这篇博客的同时，AWS Neptune图形数据库最近向公众开放。

什么是图（graph）？

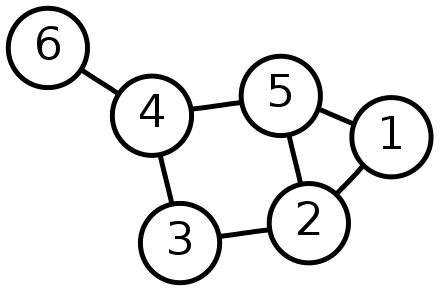
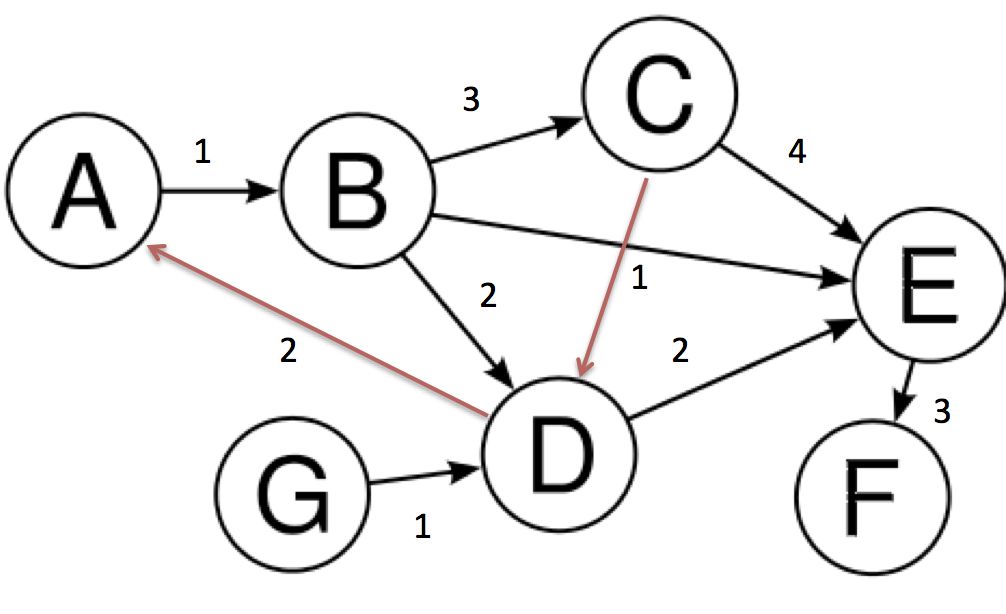
图（graph）是互相连接的节点的有限集合，这些节点互相之间由边连接。在下面的图中，每个数字代表一个节点，其中的线就是连接节点的边。

节点

一个节点是图中被连接的对象，也可以称为“顶点”。节点应该有唯一的标识，例如名字或者id。例如，在社会图形中，一个节点可以表示一个人。在计算机网络中，不同机器是不同的节点，他们的IP地址或主机名可以是节点的唯一标识物。

边

两节点之间的叫做“边（edge）”，它也可以被称为“弧线”或“线”。边可以是定向的也可以是非定向的（undirected），稍后我们会作介绍。

边也可以储存信息，在社会图形中，它们可以存储类似两人连接时长的信息。在计算机网络中，它们可以存储通讯协定等信息。

关联

关联顶点

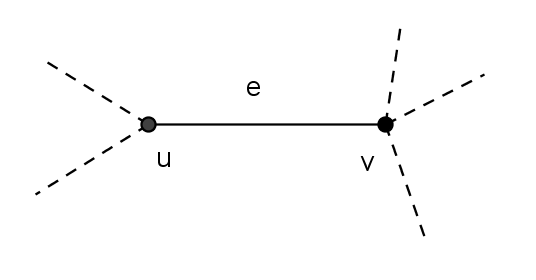
关联顶点是边所连接的顶点，再上图中，边e的关联顶点就是{U, V}

关联边

关联边是连接两顶点的边，也就是说{U, V}的关联边是e。

这里附上相关科普链接：

• 维基百科：https://proofwiki.org/wiki/Definition:Incident(GraphTheory)/Undirected_Graph)

• Stack Overflow：https://stackoverflow.com/a/16886038

图的种类

图共有两个主要类别：有向图和无向图。接下来我们就这两种图展开讲解。

无向图

无向图是互相连接的图，但在这之中没有固定的方向，节点之间也没有方向。无向图的一个例子就是LinkedIn，用户之间可能互相连接，但是他们的关系没有方向。无向图可以用来表示组成图形的无序对。

单向图

有向图又分为两种，第一种是单向图，顾名思义，这种图形与单一方向有关。其中一个例子是组织等级。比如员工都有老板，但这个关系不能颠倒。

有向图可以用来表示有顺序的对子。这里的边可以称为“有向边、箭头或有向弧线、线条等等。这样的图也常被称为定向图（oriented graph）。

双向图

双向图也是有向图的一种，其中一个例子就是Twitter等社交网络，你可以关注某人，他/她也可以反过来关注你。在这种情况中，二者的关系可以使双向的，但也不一定全部双向。

图形矩阵

不同类型的矩阵可以用来表示一张图的信息。这些矩阵可以用来计算不同信息和进行高效的检索。重要的是要注意，一个单一矩阵也许是图中的同构。这表示有关图的所有信息可能不会在一个矩阵中展示出来。例如对角线矩阵可以表示入边（incoming edges）的数量，但不能表示连接了哪些节点。

邻接矩阵

邻接矩阵是一个正方形矩阵，它可以表示哪些节点是连接着的，1表示连接，0表示不连接。在一张无向图中，如上所示，矩阵是对称的。在有向图中，邻接矩阵会用1表示入边的方向，其他用0表示，所以矩阵一般不对称。

编码的挑战

我在一次面试时接触到了邻接矩阵在编码中的问题，这个挑战是在一个3×3的矩阵中随机填入1—9随机数字，不能重复。然后确定几个随机数字的顺序，计算要在这个3×3网格上到达这几个数字需要多少个步骤，其中穿过位置的顺序也是随机的。一个相邻的位置是1步，否则就算2步。

下面是这个问题的具体例子：

# Rando 3x3 grid
[[2, 5, 9],
 [1, 8, 3],
 [4, 6, 7]]
How may steps does it take to traverse [2, 5, 8, 3, 4]?
Can you take any random grid and also random sequence and comput this?

将这个3×3矩阵中的数据下载到相邻矩阵中后就可以解决，网格中相邻的位置是相互连接的，相邻矩阵可以用作查询，解决需要多少步的问题。

度数矩阵

一个度数矩阵是表示顶点度数的对角线矩阵。顶点的度数是它的关联边的数量，顶点在行和列中表示。

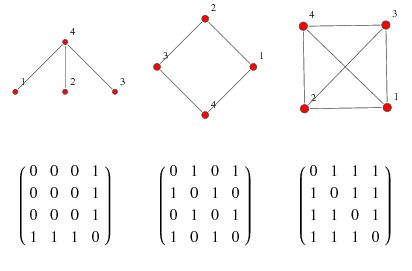
关联矩阵

下面的矩阵表示的就是上方的图，其中竖列是边，横排是节点。竖列中的1表示顶点{1, 2}的关联边e1，e2是{1, 3}的关联边，以此类推。

[[1, 1, 1, 0],
 [1, 0, 0, 0],
 [0, 1, 0, 1],
 [0, 0, 1, 1]]

关联矩阵表示的是哪条边连接的哪些节点，关联边用1表示，其他都是0。如果顶点的数量和节点数量一致，那么关联矩阵就是正方形。

有向关联矩阵

对单向图来说，-1表示出边，1表示入边，其他是0。

对双向图来说，它和单向关联矩阵一样，除了节点间入边和出边的数据用2表示。

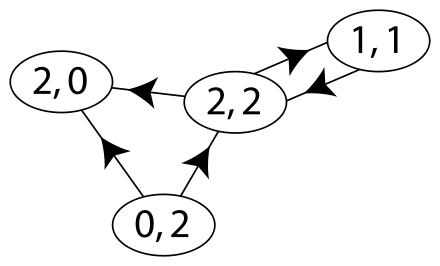
邻接列表

对于上面的图，可以用下面的矩阵表示，横排表示一个节点，竖列表示连接的节点值。

[[2, 3, 4],
 [1],
 [1, 4],
 [1, 3]]

相邻列表列出了节点相邻的节点。第一排的[2, 3, 4]是节点1的相邻节点；第二排的[1]是节点2的相邻节点，以此类推。

补充阅读

图形数据结构和算法：https://www.geeksforgeeks.org/graph-data-structure-and-algorithms/

• 图像算法的综合内容

Neo4j图形算法：https://github.com/neo4j-contrib/neo4j-graph-algorithms

• Neo4j记录了超过300中用于图形数据库的算法

有向循环图：https://en.wikipedia.org/wiki/Directedacyclicgraph

• 这是单向图类别里有趣的一种类型，也有一些软件框架利用的是这种图。

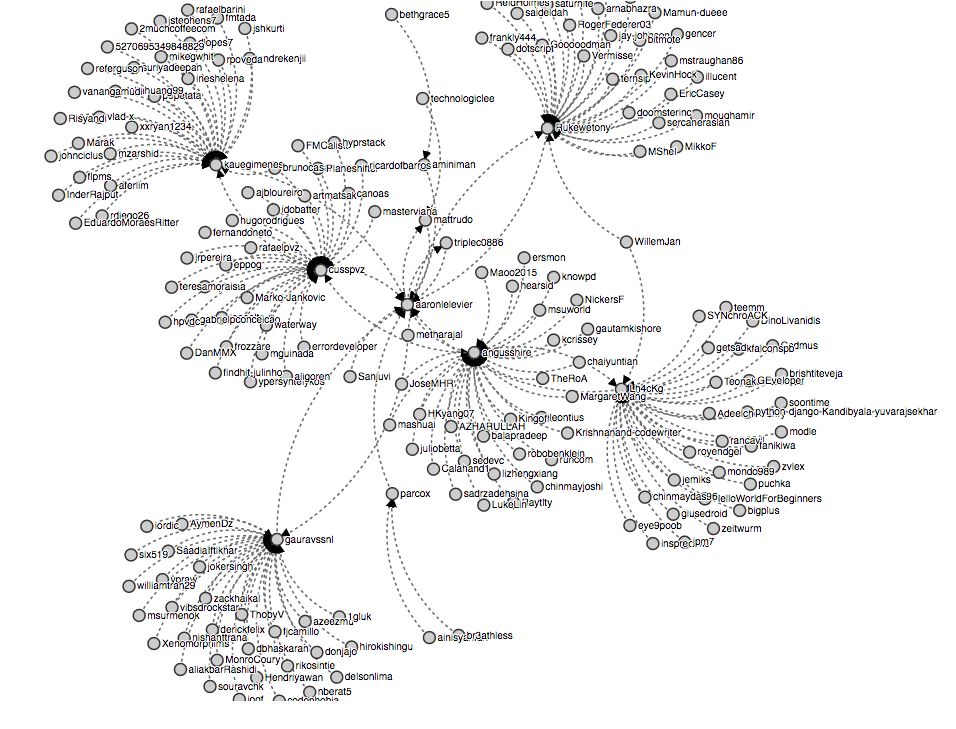
项目案例

这是我做的一个项目的demo，用的是Neo4j、D3hs和Python 多线程表示的GitHub上的关注者，是一个双向图。链接在此：https://github.com/aaronlelevier/neo4j-github-followers

结论

图论非常有趣很多领域都用到了它，例如社交网络、机器学习、决策树等等。这篇文章仅仅是一个快速介绍，在这之后还有许多关于图论的子类，感兴趣的同学可以查看文中推荐的资料和其他资源。感谢阅读！

原文地址：https://aaronlelevier.github.io/intro-to-graphs/