有向图的环和有向无环图

   本篇主要分享关于有向图的环和有向无环图（DAG，估计做大数据的同学到处都可以看到），所以相关概念我就不做详细介绍了。

 

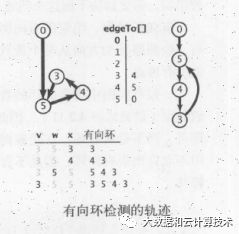
  用有向图中各个节点代表着一个又一个的任务，而其中的方向代表的任务的执行顺序。而方向代表着这个在执行这个任务之前必须完成其他节点，例如上图中在5执行必须执行3和0 节点。

   所以可以想到有向图中有向环的检测非常重要，例如上面 要是5之前 3要执行，3之前4要执行，4之前5要执行，那么着三个限制条件永远事不可能被执行的，要是一个优先级限制的问题中存在有向环，那么这个问题肯定是无解的。

   有向环的检测的理念是我们找到了一条边v-》w  要是w已经存在在栈中，就找到了一个环，因为栈中表示的是一条有w-》v的路径，而v-》w正好补全了这个环。也就是存在有向环。所以这个优先任务是有问题的。

public class DirectedCycle {
   private boolean[] marked;
   private int[] edgeTo;
   private Stack<Integer> cycle;
   private boolean[] onStack;

   public DirectedCycle(Digraph G) {
      onStack = new boolean[G.V()];
      edgeTo = new int[G.V()];
      marked = new boolean[G.V()];
      for (int v = 0; v < G.V(); v++) {
         if (!marked[v]) {
            dfs(G, v);
         }
      }
   }

   private void dfs(Digraph G, int v) {
      onStack[v] = true;
      marked[v] = true;
      for (int w : G.adj(v)) {
         if (this.hasCycle()) {
            return;
         } else if (!marked[w]) {
            edgeTo[w] = v;
            dfs(G, w);
         } else if (onStack[w]) {
            cycle = new Stack<Integer>();
            for (int x = v; x != w; x = edgeTo[x]) {
               cycle.push(x);
            }

            cycle.push(w);
            cycle.push(v);
         }
      }
      onStack[v] = false;
   }

   public boolean hasCycle() {
      return cycle != null;
   }

   public Iterable<Integer> cycle() {
      return cycle;
   }
}

猜你喜欢

#大数据和云计算机技术社区#博客精选（2017）

NoSQL 还是 SQL ？这一篇讲清楚

阿里的OceanBase解密

#大数据和云计算技术#: "四有"社区介绍

大数据和云计算技术周报（第56期）

新数仓系列：Hbase周边生态梳理（1）

《大数据架构详解》第2次修订说明

简单梳理跨数据中心数据库

云观察系列：漫谈运营商公有云发展史

云观察系列：百度云的一波三折

云观察系列：阿里云战略观察

超融合方案分析系列（7）思科超融合方案分析

加入技术讨论群

《大数据和云计算技术》社区群人数已经3000+，欢迎大家加下面助手微信，拉大家进群，自由交流。

喜欢QQ群的，可以扫描下面二维码：

欢迎大家通过二维码打赏支持技术社区（英雄请留名，社区感谢您，打赏次数超过108+）：